论文地址:https://arxiv.org/pdf/2310.11454.pdf
相关博客
【自然语言处理】【大模型】VeRA:可调参数比LoRA小10倍的低秩微调方法
【自然语言处理】【大模型】MPT模型结构源码解析(单机版)
【自然语言处理】【大模型】ChatGLM-6B模型结构代码解析(单机版)
【自然语言处理】【大模型】BLOOM模型结构源码解析(单机版)
【自然语言处理】【大模型】极低资源微调大模型方法LoRA以及BLOOM-LORA实现代码
【自然语言处理】【大模型】DeepMind的大模型Gopher
【自然语言处理】【大模型】Chinchilla:训练计算利用率最优的大语言模型
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型
一、简介
LoRA是降低微调LLM时降低可训练参数的一种方法,但是将其应用在更大的模型仍然面临着挑战。本文提出了了一种基于向量的随机矩阵适配(VeRA,Vector-based Random Matrix Adaptation)。与LoRA相比,其可以将训练参数的数量减少10倍,但保持相同的性能。
二、相关工作
1. LoRA
LoRA为LLM微调带来的计算挑战提供了一种新颖的解决方案。该方法使用低秩矩阵来近似微调过程中的权重变化,从而有效地减低训练所需的参数量。其还可以使用量化模型权重来进一步降低要求。与基于adapter的微调方法相比,LoRA在部署时不会产生额外的推理时间成本,因此训练矩阵可以和权重合并。
AdaLoRA扩展了LoRA方法,在微调过程中引入了低秩矩阵的动态调整。核心思想是通过基于重要性度量来选择性的修剪矩阵中不太重要的分量,从而优化参数预算的分配。
2. 现有方法的参数效率
虽然LoRA这样的方法在微调性能方法展现出了显著的改善,但是仍然需要大量的可训练参数。基于Aghajanyan等人的研究,内在维度的上限比这种方法中通常使用的秩要小的多。因此,参数量可以进一步减少。虽然AdaLoRA通过动态分配参数,从而进一步减少了可微调参数。但是,我们认为存在另一种可以显著减少可训练参数,且效果不会下降的方法。
3. 随机模型和投影
使用随机矩阵和投影来提高模型效率的概念已经得到了多方面研究的支持。Frankle&Carbin发现随机初始化的神经网络中包含训练时能够达到高性能的子网络。此外,Ramanujan等人了存在的子网络即使没有训练也能够取得令人印象深刻的结果。Aghajanyan等人展示了仅训练少量参数,随机投影会完整空间,能够实现全参数模型效果的90%。其他的一些工作也表明,冻结的随机初始化模型加上小部分的微调,表现出奇的好。
三、方法
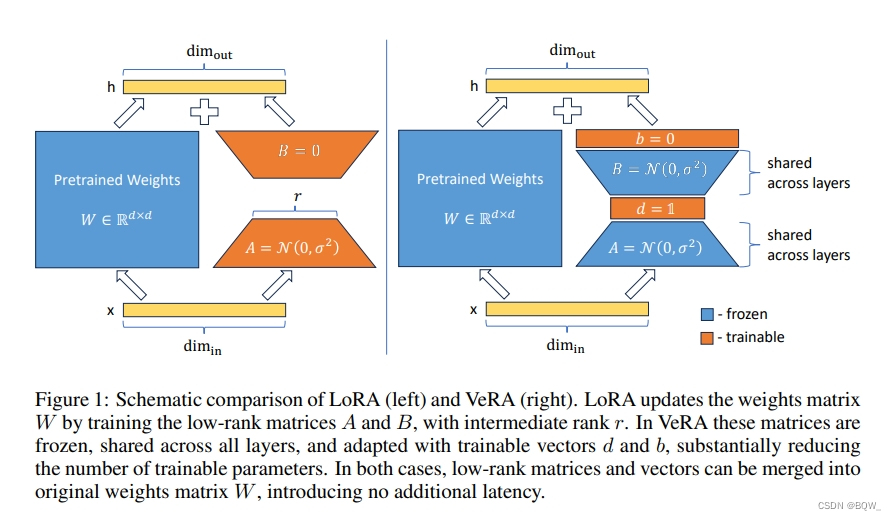
VeRA的核心创新是低秩矩阵的重参数化。具体来说,冻结一对随机初始化的矩阵,这些矩阵在所有适配层之间共享,然后引入可以逐层自适应的可训练缩放向量。如上图1所示,类似于LoRA,训练的缩放向量和低秩矩阵可以合并至原始权重中,从而消除额外的推理延迟。
1. 方法介绍
LoRA微调两个低秩矩阵的乘积来适应LLM。正式来说,对于预训练权重矩阵 W 0 ∈ R m × n W_0\in\mathbb{R}^{m\times n} W0∈Rm×n,权重更新矩阵被约束为低秩分解,即
h = W 0 x + Δ W x = W 0 x + B A ‾ X (1) h=W_0x+\Delta Wx=W_0x+\underline{BA}X\tag{1} h=W0x+ΔWx=W0x+BAX(1)
其中带有下划线的参数通过梯度更新。这种近似可以使得模型保持原始权重 W 0 W_0 W0冻结,同时仅优化低秩矩阵 A A A和 B B B。它们的尺寸要远比原始矩阵小。 A A A的形状是 m × r m\times r m×r, B B B的形状是 r × n r\times n r×n,而 r ≪ min ( m , n ) r\ll\min(m,n) r≪min(m,n)。相比, VeRA \text{VeRA} VeRA为
h = W 0 + Δ W x = W 0 x + Λ b ‾ B Λ d ‾ A x (2) h=W_0+\Delta Wx=W_0x+\underline{\Lambda_b}B\underline{\Lambda_d}Ax\tag{2} h=W0+ΔWx=W0x+ΛbBΛdAx(2)
在本方法中, B B B和 A A A是冻结、随机且跨层共享的,而缩放向量 b b b和 d d d是可训练的,形式上表达为对角矩阵 Λ b \Lambda_b Λb和 Λ d \Lambda_d Λd。在这种情况下, B ∈ R m × r B\in\mathbb{R}^{m\times r} B∈Rm×r和 A ∈ R r × n A\in\mathbb{R}^{r\times n} A∈Rr×n不需要是低秩的。这是因为这两个矩阵是静态的,并且不需要存在这些值。相反,由于 d ∈ R 1 × r d\in\mathbb{R}^{1\times r} d∈R1×r,改变 r r r仅会线性增加可训练参数的数量。
2. 参数计数
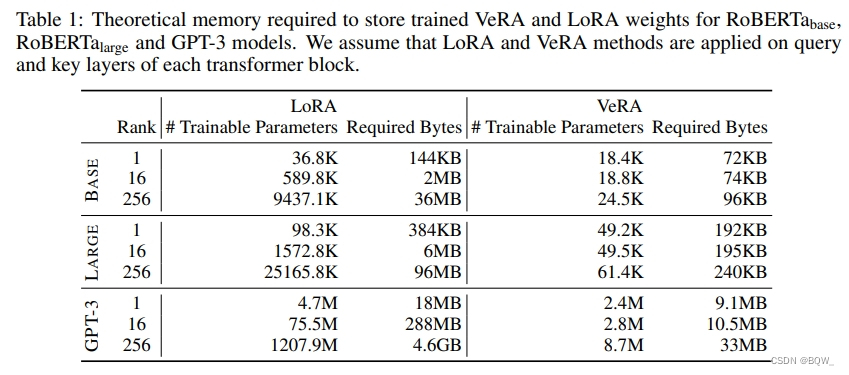
使用 L t u n e d L_{tuned} Ltuned表示微调层的数量, d m o d e l d_{model} dmodel表示这些层的维度。VeRA的可训练参数数量为
∣ Θ ∣ = L t u n e d × ( d m o d e l + r ) (3) |\Theta|=L_{tuned}\times(d_{model}+r)\tag{3} ∣Θ∣=Ltuned×(dmodel+r)(3)
而LoRA的可微调参数为
∣ Θ ∣ = 2 × L t u n e d × d m o d e l × r (4) |\Theta|=2\times L_{tuned}\times d_{model}\times r\tag{4} ∣Θ∣=2×Ltuned×dmodel×r(4)
具体来说,对于最低的秩( r = 1 r=1 r=1),VeRA大约需要LoRA一半的可训练参数。此外,随着秩的增加,VeRA的可训练参数一次仅增加 L t u n e d L_{tuned} Ltuned,而LoRA则增加 2 L t u n e d d m o d e l 2L_{tuned}d_{model} 2Ltuneddmodel。对于极大的模型,这种参数效率则极为显著,例如GPT-3有96个注意力层且hidden size为12288。
VeRAA的主要优势是存储训练的权重占用非常小的存储空间。因此随机冻结矩阵可以从随机数生成器种子中重新生成,所以这些矩阵不需要存储。这大大减少了内存的需求,现有的内存需要仅限于训练向量 b b b和 d d d以及单个随机数种子所需要的字节。与LoRA相比的内存效率如表1所示。
3. 初始化策略
共享矩阵。利用Kaiming初始化方法来初始化冻结低秩矩阵 A A A和 B B B。通过基于矩阵维度的缩放至,其能确保 A A A和 B B B的矩阵乘积对所有秩保存一致的方差,从而消除对每个秩的学习率进行微调的需求。
缩放向量。缩放向量 b b b被初始化为0,这与LoRA中矩阵 B B B的初始化是一致的,能确保权重矩阵在第一次前向传播时不受影响。缩放向量 d d d的所有元素使用单个非零值进行初始化,从而引入了一个新的超参数。调整该超参数可以带来更好的效果。
图1展示了VeRA中低秩矩阵和缩放向量的初始化示例。具体来说看,使用正态分布来初始化低秩矩阵,并使用1来初始化 d d d向量。
四、实验
baselines包括:全参微调、Bitfit(仅微调bias向量,其他参数保存固定)、Adapter tuning、LoRA。
1. GLUE Benchmark
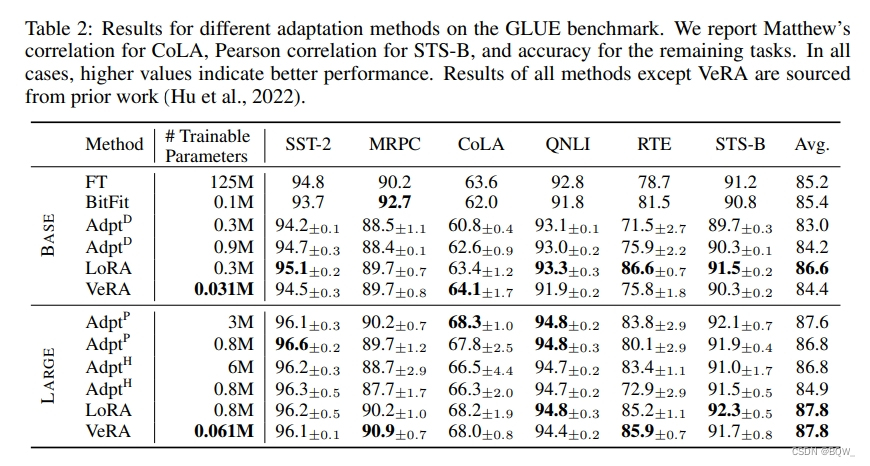
2. E2E Benchmark
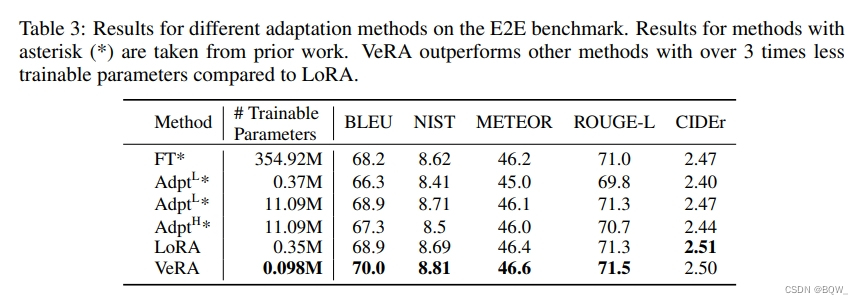
3. LLaMA-2-7B指令遵循

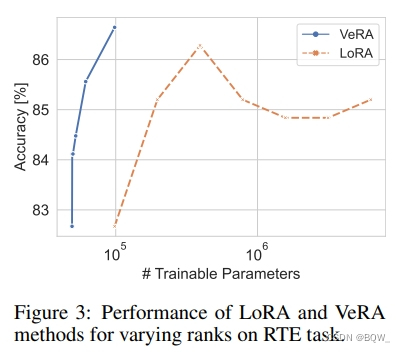
4. 可训练参数数量的影响










:笔迹检验的程序和方法)



CSS 盒子模型)




