使用求2个字符串最短编辑距离动态规划算法实现 git diff 算法 java 实现

测试类 MyDiffTest.java：
import java.io.BufferedReader;
import java.io.FileReader;
import java.util.ArrayList;
import java.util.List;public class MyDiffTest {private static String path = "\\xxx\\";private static List<String> lines_v1 = readFile2List( path + "DemoClass1.java" );private static List<String> lines_v2 = readFile2List( path + "DemoClass2.java" );public static void main(String[] args) {/*lines_v1 = new ArrayList<>();lines_v2 = new ArrayList<>();lines_v1.add( "m" );lines_v1.add( "o" );lines_v1.add( "t" );lines_v1.add( "h" );lines_v1.add( "e" );lines_v1.add( "r" );lines_v2.add( "m" );lines_v2.add( "o" );lines_v2.add( "n" );lines_v2.add( "s" );lines_v2.add( "t" );lines_v2.add( "e" );lines_v2.add( "r" );*/int[][] dp =  calculateMinimumTransferWay(lines_v1, lines_v2);int index1 = lines_v1.size() - 1;int index2 = lines_v2.size() - 1;System.out.println( "最短编辑距离：" +  dp[index1][index2] );List<String> result = new ArrayList<>();while ( index1 >= 0 && index2 >= 0 ){String line_v1 = lines_v1.get(index1);String line_v2 = lines_v2.get(index2);if( line_v1.equals( line_v2 ) ){// v1：...a// v2：...a// 此时，v1 和 v2 的当前行相同，原封不懂的输出，表示没有改动result.add( "  " + line_v1 );index1--;index2--;}else {// v1：...a// v2：...b// 此时，v1版本的当前行和 v2版本的当前行不相同，所以v1转化为v2过程中，对 行a、行b的操作有3种可能：新增行b、删除行a// v1：...a// v2： ...  b// 如果此时的编辑距离是最小的，则v2版本需要新增 行bint sed1 = dp[index1][index2 - 1] + 1; // ps：sed 是 shortest edit distance 的缩写// v1： ...  a// v2：...b// 如果此时的编辑距离是最小的，则v2版本需要删除 行aint sed2 = dp[ index1 - 1 ][ index2 ] + 1;// v1： ...  a// v2： ...  b// 如果此时的编辑路基是最小的，则v2版本需要将 删除行a+新增行b( 一共2步操作 )int sed3 = dp[ index1 - 1 ][ index2 - 1 ] + 2;int sed = Math.min(Math.min(sed1, sed2), sed3);if( sed1 == sed ){result.add( "+ " + line_v2 );index2--;}else if( sed2 == sed ){result.add( "- " + line_v1 );index1--;}else if( sed3 == sed ){result.add( "+ " + line_v2 );result.add( "- " + line_v1 );index1--;index2--;}}}while ( index1 >= 0 ){// v1 还剩下的一些 "首行们" 都是需要被删除的行，因为v2版本没有result.add( "- " + lines_v1.get( index1 ) );index1--;}while ( index2 >= 0 ){// v2 还剩下的一些 "首行们" 都是需要被添加的行，因为v1版本没有result.add( "+ " + lines_v2.get( index2 ) );index2--;}for (int i = ( result.size() - 1 ); i >= 0;i-- ) {System.out.println( result.get( i ) );}}private static List<String> readFile2List( String filePath ){BufferedReader reader = null;try {List<String> lines = new ArrayList<>();reader = new BufferedReader(new FileReader(filePath));String line = reader.readLine();while (line != null) {lines.add( line );line = reader.readLine();}return lines;} catch (Exception e) {e.printStackTrace();return null;} finally {if (reader != null) {try {reader.close();} catch (Exception e) {e.printStackTrace();}}}}private static int[][] calculateMinimumTransferWay(List<String> lines_v1, List<String> lines_v2 ){int size_v1 = lines_v1.size();int size_v2 = lines_v2.size();int[][] dp = new int[ size_v1 ][ size_v2 ];for (int index1 = 0; index1 < size_v1; index1++) {String line_v1 = lines_v1.get( index1 );for (int index2 = 0; index2 < size_v2; index2++) {String line_v2 = lines_v2.get( index2 );if( index1 == 0 ){if( index2 == 0 ){if( line_v1.equals( line_v2 ) ){// v1：a// v2：a// 无需任何操作dp[ index1 ][ index2 ] = 0;}else {// 不相同,需要 1 步删除操作，1步插入操作// v1：a// v2：bdp[ index1 ][ index2 ] = 2;}}else {if( getFirstEqualIndex( lines_v2,line_v1,0,index2 ) != -1 ){// v1：      a// v2：...a...// 需要 index2 步插入操作dp[ index1 ][ index2 ] = index2;}else {// v1：      a// v2：...b...// 需要1步删除操作，index2 + 1步插入操作dp[ index1 ][ index2 ] = index2 + 2;}}}else {if( index2 == 0 ){if( getFirstEqualIndex(lines_v1, line_v2, 0, index1) != -1 ){// v1：...a...// v2：      a// 需要 index1 步删除操作dp[ index1 ][ index2 ] = index1;}else {// v1：...a...// v2：      b// 需要 index1 + 1 步删除操作，1步插入操作dp[ index1 ][ index2 ] = index1 + 2;}}else {if( line_v1.equals( line_v2 ) ){// v1：...a// v2：...adp[ index1 ][ index2 ] = dp[index1 - 1][index2 - 1];}else {// v1：...a// v2：...b// sed means "shorest edit distance"int sed1 = dp[index1 - 1][index2];int sed2 = dp[index1 ][index2 - 1];int sed3 = dp[index1 - 1][index2 - 1];int sed = Math.min( Math.min( sed1,sed2 ),sed3 );if( sed1 == sed || sed2 == sed ){dp[ index1 ][ index2 ] = sed + 1;}else {dp[ index1 ][ index2 ] = sed + 2;}}}}}}return dp;}private static int getFirstEqualIndex(List<String> lines, String targetLine, int beginIndex, int endIndex) {for (int i = beginIndex; i <=endIndex ; i++) {if( targetLine.equals( lines.get( i ) ) ){return i;}}return -1;}
}

旧版本文本文件 DemoClass1.java：

import lombok.extern.slf4j.Slf4j;
import org.apache.commons.text.similarity.LevenshteinDistance;@Slf4j
public class DemoClass1 {private static final LevenshteinDistance LEVENSHTEIN_DISTANCE = LevenshteinDistance.getDefaultInstance();public static String null2emptyWithTrim( String str ){if( str == null ){str = "";}str = str.trim();return str;}public static String requiredStringParamCheck(String param, String paramRemark) {param = null2emptyWithTrim( param );if( param.length() == 0 ){String msg = "操作失败，请求参数 \"" + paramRemark + "\" 为空";log.error( msg );throw new BusinessLogicException( msg );}return param;}public static double calculateSimilarity( String str1,String str2 ){int distance = LEVENSHTEIN_DISTANCE.apply(str1, str2);double similarity = 1 - (double) distance / Math.max(str1.length(), str2.length());System.out.println("相似度：" + similarity);return similarity;}
}

新版本文本文件 DemoClass2.java：

import lombok.extern.slf4j.Slf4j;
import org.apache.commons.text.similarity.LevenshteinDistance;@Slf4j
public class DemoClass2 {private static final LevenshteinDistance LEVENSHTEIN_DISTANCE = LevenshteinDistance.getDefaultInstance();private static final LevenshteinDistance LEVENSHTEIN_DISTANCE1 = LevenshteinDistance.getDefaultInstance();private static final LevenshteinDistance LEVENSHTEIN_DISTANCE2 = LevenshteinDistance.getDefaultInstance();public static String null2emptyWithTrim( String str ){// if( str == null ){//     str = "";// }// str = str.trim();return str;}public static String requiredStringParamCheck(String param, String paramRemark) {return null;}public static double calculateSimilarity( String str1,String str2 ){try {int distance = LEVENSHTEIN_DISTANCE.apply(str1, str2);double similarity = 1 - (double) distance / Math.max(str1.length(), str2.length());return similarity;}catch ( Exception e ){e.printStackTrace();return 0d;}}
}

测试输出：

import com.goldwind.ipark.common.exception.BusinessLogicException;import lombok.extern.slf4j.Slf4j;import org.apache.commons.text.similarity.LevenshteinDistance;@Slf4j
- public class DemoClass1 {
+ public class DemoClass2 {private static final LevenshteinDistance LEVENSHTEIN_DISTANCE = LevenshteinDistance.getDefaultInstance();
+     private static final LevenshteinDistance LEVENSHTEIN_DISTANCE1 = LevenshteinDistance.getDefaultInstance();
+     private static final LevenshteinDistance LEVENSHTEIN_DISTANCE2 = LevenshteinDistance.getDefaultInstance();public static String null2emptyWithTrim( String str ){
-         if( str == null ){
-             str = "";
-         }
-         str = str.trim();
+         // if( str == null ){
+         //     str = "";
+         // }
+         // str = str.trim();return str;}public static String requiredStringParamCheck(String param, String paramRemark) {
-         param = null2emptyWithTrim( param );
-         if( param.length() == 0 ){
-             String msg = "操作失败，请求参数 \"" + paramRemark + "\" 为空";
-             log.error( msg );
-             throw new BusinessLogicException( msg );
-         }
-         return param;
+         return null;}public static double calculateSimilarity( String str1,String str2 ){
-         int distance = LEVENSHTEIN_DISTANCE.apply(str1, str2);
-         double similarity = 1 - (double) distance / Math.max(str1.length(), str2.length());
-         System.out.println("相似度：" + similarity);
-         return similarity;
+         try {
+             int distance = LEVENSHTEIN_DISTANCE.apply(str1, str2);
+             double similarity = 1 - (double) distance / Math.max(str1.length(), str2.length());
+             return similarity;
+         }catch ( Exception e ){
+             e.printStackTrace();
+             return 0d;
+         }}}

求做小编辑距离的时候，我这里不允许编辑操作，通常的求最小编辑距离一共允许三种操作( 删除、新增、编辑 )，其中一个编辑操作和删除、新增操作的权重都算作一步，我这里不允许编辑操作，比如迫不得已必须用编辑操作时，例如将a 行变为b行，我们必须先删除，后增加，其实等效于允许编辑操作，但是编辑操作权重大一些，为什么这样规定呢？

如上所示，新版本相对于旧版本来说是连续的修改了多行，我们人眼比较习惯这种差异比较后的输出：

而不是这种输出( 虽然逻辑上也对 )：

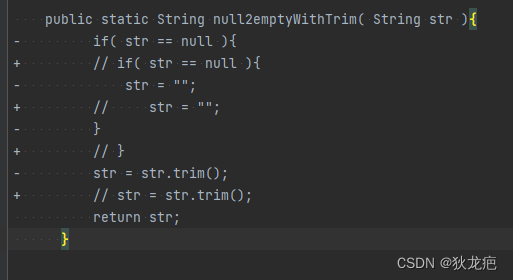
如果允许编辑操作( 或者编辑操作的权重和删除、新增操作一样时 )，就可能会出现这种情况，整块整块的修改给当做每一行来一个编辑操作。如果不允许编辑操作( 其实等价于将编辑操作的权重设置为删除或者插入操作的2倍 )，那么当出现整块的修改时，差异化比较时，被当做多个单行的修改的概率就被降低了，因为那样的话编辑次数会更多，所以会优先的视为多行的删除( 块删除 )操作和多行的新增( 块新增 )。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/194410.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Springboot启动原理解析

Springboot启动原理解析

我们开发任何一个Spring Boot项目&#xff0c;都会用到如下的启动类 SpringBootApplication public class Application {public static void main(String[] args) {SpringApplication.run(Application.class, args);} } 从上面代码可以看出&#xff0c;Annotation定义&#x…
阅读更多...
网络运维与网络安全 学习笔记2023.12.3

网络运维与网络安全 学习笔记2023.12.3

网络运维与网络安全 学习笔记 第三十三天 今日目标 目录-文件基本管理、vim文本编辑、用户账号管理 组账号管理、归属控制、权限控制 目录-文件基本管理 ls 列目录及文档属性 ls - List 格式:ls[选项]…[目录或文件路径] 1.如果不以/开始,表示相对路径(省略了当前所在位置…
阅读更多...
go并发编程（中）

go并发编程（中）

目录 一、并发安全性 1.1 变量并发安全性 1.2 容器并发安全性 二、多路复用 三、协程常见的面试题 3.1交替打印奇数偶数 一、并发安全性 1.1 变量并发安全性 这个和C中并发安全是一样的&#xff0c;主要是多个线程对临界资源的同时访问&#xff0c;最经典的就是 n操作…
阅读更多...
智慧公厕新风系统是什么？具体作用？

智慧公厕新风系统是什么？具体作用？

大家好&#xff0c;你们可曾在公厕里遇到那个臭味怪兽&#xff0c;闻得让人头晕目眩&#xff1f;别怕&#xff0c;我们有一把利剑&#xff0c;叫做“智慧公厕新风系统”&#xff01;不仅是空气净化器的升级版&#xff0c;还有一大堆高级功能等着你来领略&#xff01; 1. 风清气…
阅读更多...
Kettle 安装配置

Kettle 安装配置

文章目录 Kettle 安装配置Kettle 安装Kettle 配置连接 Hive Kettle 安装配置 Kettle 安装 在安装Kettle之前&#xff0c;需要确定已经安装Java运行环境。Kettle需要Java的支持才能运行&#xff0c;JDK的版本最好是8.x的太新的也会出现bug。Kettle的7.1版本的太旧了&#xff0…
阅读更多...
MQ - KAFKA 基础篇

MQ - KAFKA 基础篇

##1、KAFKA的核心组件/API Producer API&#xff0c;它允许应用程序向一个或多个 topics 上发送消息记录 Consumer API&#xff0c;允许应用程序订阅一个或多个 topics 并处理为其生成的记录流 Streams API&#xff0c;它允许应用程序作为流处理器&#xff0c;从一个或多个主…
阅读更多...
【springboot】启动失败 Failed to start bean ‘webServerStartStop‘

【springboot】启动失败 Failed to start bean ‘webServerStartStop‘

lsof -i&#xff1a;xxx 发现端口被占用 kill掉该进程
阅读更多...
代码随想录算法训练营第五十三天【动态规划part14】 | 1143.最长公共子序列、1035.不相交的线、53. 最大子序和

代码随想录算法训练营第五十三天【动态规划part14】 | 1143.最长公共子序列、1035.不相交的线、53. 最大子序和

1143.最长公共子序列 题目链接 力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台 求解思路 动规五部曲 1.确定dp数组及其下标含义&#xff1a; dp[i][j]&#xff1a;长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序…
阅读更多...
OpenWrt作为旁路由（网关）配置

OpenWrt作为旁路由（网关）配置

目录 背景前提条件环境操作步骤物理层连接设置与主路由同一网段禁用IPv6取消LAN接口桥接防火墙配置 背景 本文简介如何配置OpenWrt&#xff0c;使其作为旁路由&#xff08;网关&#xff09;运行。 旁路由大概有以下这几种工作方式&#xff1a; 主路由开DHCP&#xff0c;网关未…
阅读更多...
一文彻底弄懂动态规划【DP】

一文彻底弄懂动态规划【DP】

动态规划是一种重要的算法&#xff0c;它能解决很多看似复杂的问题&#xff0c;关键在于找到问题的子问题结构&#xff0c;并根据子问题的解决方式来解决原问题。首先要了解的是动态规划的基本思想&#xff1a; 动态规划的基本思想是&#xff1a;将一个复杂的问题分解为一系列…
阅读更多...
深层神经网络（第四周）

深层神经网络（第四周）

这里省略了深层神经网络的前向传播和反向传播&#xff0c;内容和之前相似&#xff0c;不做过多描述。若今后需要&#xff0c;可以再补习。 一、为什么使用深层表示 解决问题时其实并不需要很大的神经网络&#xff0c;但是得有深度&#xff0c;得有比较多的隐藏层。这是为什么…
阅读更多...
字符串转换整数

字符串转换整数

字符串转换整数 描述 : 请你来实现一个 myAtoi(string s) 函数&#xff0c;使其能将字符串转换成一个 32 位有符号整数&#xff08;类似 C/C 中的 atoi 函数&#xff09;。 函数 myAtoi(string s) 的算法如下&#xff1a; 读入字符串并丢弃无用的前导空格检查下一个字符&am…
阅读更多...
select选择框里填充图片，下拉选项带图片

select选择框里填充图片，下拉选项带图片

遇到一个需求&#xff0c;选择下拉框选取图标&#xff0c;填充到框里 1、效果展示 2、代码 <el-form-item label"工种图标" class"Form_icon Form_label"><el-select ref"select" :value"formLabelAlign.icon" placeholder&…
阅读更多...
Python第三方库版本管理（管理虚拟环境）

Python第三方库版本管理（管理虚拟环境）

序言 最近使用python发现会有使用不同项目时需要的三方包依赖版本不同&#xff0c;如果各个项目相互切换&#xff0c;那么会经常需要更新版本。比如numpy当前版本时1.26.2&#xff0c;需要它小于版本1.21&#xff0c;有没有像Java一样通过Maven依赖管理中的版本控制去管理这些…
阅读更多...
Redis--12--Redis分布式锁的实现

Redis--12--Redis分布式锁的实现

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 Redis分布式锁最简单的实现如何避免死锁&#xff1f;锁被别人释放怎么办&#xff1f;锁过期时间不好评估怎么办&#xff1f;--看门狗分布式锁加入看门狗 redissonRe…
阅读更多...
什么是跨站脚本攻击

什么是跨站脚本攻击

跨站脚本攻击 1. 定义2. 跨站脚本攻击如何工作3. 跨站脚本攻击类型4. 如何防止跨站脚本攻击 1. 定义 跨站脚本攻击&#xff08;Cross-site Scripting&#xff0c;通常称为XSS&#xff09;&#xff0c;是一种典型的Web程序漏洞利用攻击&#xff0c;在线论坛、博客、留言板等共享…
阅读更多...
数据结构和算法-线索二叉树中的线索化和在线索二叉树中找前驱后继

数据结构和算法-线索二叉树中的线索化和在线索二叉树中找前驱后继

线索二叉树的概念 找到某个节点得按照遍历得到的序列开始遍历才能遍历全部节点&#xff0c;非常繁琐 中序线索二叉树 线索二叉树的存储结构 先序线索二叉树 后序线索二叉树 三种线索二叉树的对比 即对应前驱后后继判断标准不同 小结 二叉树的线索化 用土办法找中序前驱 当…
阅读更多...
Prefix-Tuning 论文概述

Prefix-Tuning 论文概述

Prefix-Tuning 论文概述 前缀调优&#xff1a;优化生成的连续提示前言摘要论文十问实验数据集模型实验结论摘要任务泛化性能 前缀调优&#xff1a;优化生成的连续提示 前言 大规模预训练语言模型(PLM)在下游自然语言生成任务中广泛采用fine-tuning的方法进行adaptation。但是f…
阅读更多...
android studio安装SDK时无法勾选

android studio安装SDK时无法勾选

这两天帮助学妹安装android studio安装SDK时无法勾选&#xff0c;记录一下最终解决办法。头大。 核心 360 问题 网上所有方法都尝试了包括挂梯子&#xff0c;改hosts&#xff0c;盘符权限等等。 最终解决下载360 使用这两个&#xff0c;DNS注意要用8.8.8.8的 成功解决
阅读更多...
超硬核解析Mybatis动态代理原理！只有接口没实现也能跑？

超硬核解析Mybatis动态代理原理！只有接口没实现也能跑？

文章目录 前言Mybatis dao层两种实现方式的对比原始Dao开发原始Dao开发的弊端 基于Mapper动态代理的开发方式 Mybatis动态代理实现方式的原理解析动态代理调用链路解析先给出链路调用结果1、调用方法的开始&#xff1a;session.getMapper2、DeaultSqlSession的getMapper3、Conf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023