1.简述
相信没有相关物理知识背景的小伙伴看到“退火”二字是一脸懵逼的...固体的退火过程指的是将固体加热至足够高的温度,再使其慢慢冷却的过程。在加热过程中,原本有序排列的内部粒子开始无序运动,此时固体的内能不断增大;而在降温过程中,粒子的排列又逐渐有序。
而物体系统总是趋向于保持能量最低的状态,理论上讲,在退火过程的降温过程中,如果降温过程足够的慢,可将每一时刻离散化,那么每一个温度下的固体都可能达到允许范围内的最小内能状态,而如何寻找该温度及状态即为模拟退火算法的核心问题。
模拟退火算法和遗传算法、粒子群算法等智能算法作为一种通用的概率算法,相关的知识可以去看看我之前的学习笔记:
Kezard:遗传算法1(GA)---基础概念及算法流程68 赞同 · 1 评论文章编辑
Kezard:粒子群(PSO)算法概念及代码实现159 赞同 · 14 评论文章编辑
该类智能算法都可用来寻找一个较大搜索空间之内的全局最优解。搜索空间之内的每一个元素都可能是问题的全局最优解,那么如何确立搜索方式、如何判断某一温度下的固体粒子内能状态便成为区分其他智能算法的核心工作。一般地,可以将温度T作为搜索空间;将实际情况中的目标函数值f看做内能E;而固体在某一温度下的状态看做问题的一个解x,即E=f(x);算法在一定的规则之下,控制温度T的降低,使固体的内能也随着最优值(内能最低)靠近,直至找到了全局最优解,就像固体退火过程一样。
如何判断内能减少?
Metropolis准则:从当前i状态发展到下一状态j,若新状态的内能小于状态i的内能,则接受j为新的状态,其对应的内能作为目前的最优解;否则,以概率] 接收该新解, 其中k为Boltzmann常数,T为目前的温度。在后续的判断过程中可加入计算机的蒙特卡罗实验模拟产生概率(随机数)。
算法设计为了寻找最小的内能,那可以对应到实际情况中的全局最小解,若要寻找全局最大值,在目标函数前添加“负号”即可。
算法基本步骤:
- 确定退火过程的温度初值 0 ,随机生成该温度下的粒子状态及一个解 0 ,计算目标函数值f即该状态下的内能 0 。
- 进入下一个冷却温度。
- 对当前的解 添加扰动,及产生个新的解 ,计算相应的内能 ,根据Metropolis准则判断是否接受新的解,更新局部最优解和全局最优解。
- 在不同的冷却温度 下,重复m次对x的扰动,即产生m个新的解,并执行2~3.
- 判断T是否已经到达了最低温度限制,一般设定为 0.01∼5 ,是则终止算法;否继续执行2~4.
算法实际上由两层循环所控制,外层循环控制降温过程的温度;内层循环控制对解x的扰动。算法的初始温度 0 较高,这样使得内能增大的初始解也可能被接受,因为能够跳出局部最小值的陷阱,然后通过慢慢的降低温度,对解不断地添加扰动,使得算法最终可能收敛到全局最优解。
前面的步骤5中谈到外层循环终止的条件为是否到达了最低温度限制,当然我们还可以引入一些提前终止降温过程的条件,比如最大寻找次数、满足最大精度设置等。
参数选择
一、控制参数T的初值 0
求解全局优化问题的随机搜索算法(例如遗传算法,粒子群算法)一般都采用全局粗略搜索与局部精细搜索相结合的策略。粗略搜索能够使得搜索过程跳出局部最优解的陷阱,而局部精细搜索便可以找到问题的全局最优解,一般而言,足够大的初值 0 才能遍历所有的可行解,过小的初值往往导致算法难以逾越局部最优解,从而不能找到全局最优解。所以在选取的时候应当适应的选取初值,并且与其他参数相协调。(我的程序中选择的初值为1000)
二、降温过程
降温参数,其取值为 0.5∼0.99 ,该参数决定了降温过程,其值选择的越大,则降温过程越慢,导致迭代次数的增加,当然更有可能寻找到全局最优解,若已经到达了热平衡,则仅需要少量的状态变换就可以达到准平衡,从而减少内层循环的长度(Markov链长度)
三、Markov链的长度(解的扰动变换次数)
选取原则是:在控制参数T的降温过程函数已选定的前提之下,从经验上来说,长度一般为 100� ,n为问题的规模。
模拟退火算法求解TSP问题的matlab求解
- TSP问题:TSP(Traveling salesman problem)即旅行商问题,旅行商希望在N个城市进行一次巡回旅行,可以恰好访问每一个城市一次,并且最终回到出发城市。并且要使得这次巡回旅行的总消耗最小(总距离或总花销等等),如何求这个路线?
- TSP的解空间S是遍历每个城市恰好一次的所有回路(回到起点),那么一个可行解即为所有城市的一个排列,则解空间可以表示为:
即为每个城市的编号,其中的每一个排列即为一个离线,所以初始解就被表示成为了一个{1,2,...,N}的随机序列。
2. 目标函数
遍历所有城市的代价最小,此处我们将代价刻画为总路径最小 即为该最短路径(TSP问题的解即为城市标号的一个排列)
3. 新解的产生
- 两点交换法:交换 ,的访问顺序
- 三变换:任选序号 之间的路径插到 �之后访问。
4. Metropolis接收准则
以新解与当前解的目标函数差(内能之差)来定义接受概率:
2.代码
主程序:
%% 用模拟退火法计算函数的最小值
clear all
f = inline('5*sin(x(1)*x(2))+x(1)^2+x(2)^2','x');
l = [-5 -5]; %下限
u = [5 5]; %上限
x0 = [-4 0];
TolFun = 1e-9;
TolX=1e-5;
kmax = 800;
%%%%用Nelder-Meat法求
[xo_nd,fo] = Opt_Nelder(f,x0,TolX,TolFun,kmax)
%%%%用matlab内置函数验证
[xos,fos] = fminsearch(f,x0)
[xou,fou] = fminunc(f,x0)
%%%%用模拟退火法求
q =0.8;
[xo_sa,fo_sa] =Opt_Simu(f,x0,l,u,kmax,q,TolFun)
子程序:
function [xo,fo] =Opt_Nelder(f,x0,TolX,TolFun,MaxIter)
%Nelder-Mead法用于多维变量的最优化问题,维数>=2.
N = length(x0);
if N == 1 %一维情况,用二次逼近计算
[xo,fo] = Opt_Quadratic(f,x0,TolX,TolFun,MaxIter);
return
end
S = eye(N);
for i = 1:N %自变量维数大于2时,重复计算每个子平面的情况
i1 = i + 1;
if i1 > N
i1 = 1;
end
abc = [x0; x0 + S(i,:); x0 + S(i1,:)]; %每一个定向子平面
fabc = [feval(f,abc(1,:)); feval(f,abc(2,:)); feval(f,abc(3,:))];
[x0,fo] = Nelder0(f,abc,fabc,TolX,TolFun,MaxIter);
if N < 3 %二维情况不需重复
break;
end
end
xo = x0;
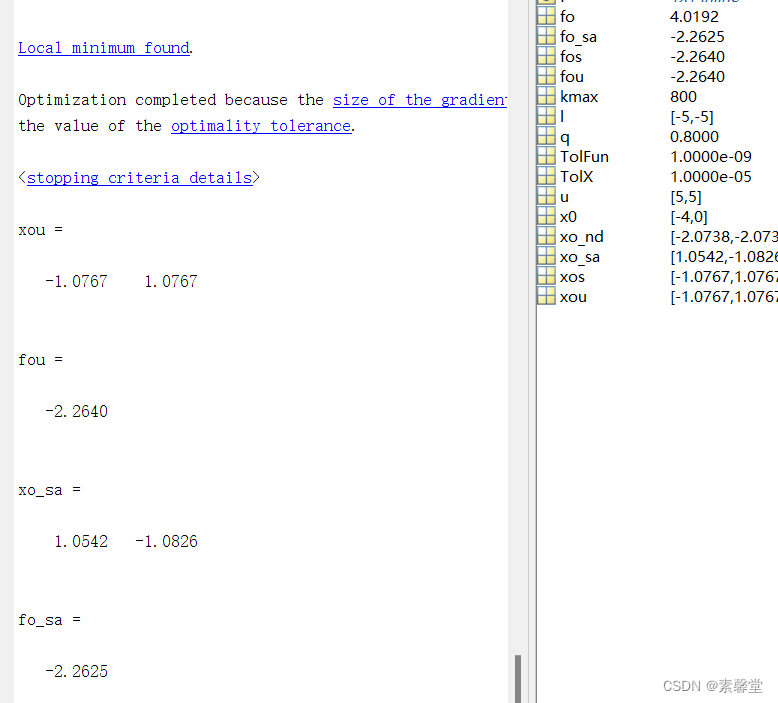
3.运行结果















)



