摘要

在金融应用中，检测时间序列数据中的异常子序列是一项重要的任务，从制造过程到医疗保健监测。异常可以指示重要的事件，例如生产故障、交付瓶颈、系统缺陷或心脏闪烁，因此是核心兴趣。由于时间序列通常很大并且表现出复杂的模式，数据科学家已经开发了各种专门的算法来自动检测这种异常模式。异常检测算法的数量和种类在过去已经显着增长，并且由于其中许多解决方案是独立开发的，并且由不同的研究社区开发，没有全面的研究系统地评估和比较不同的方法。出于这个原因，为给定的异常检测任务选择最佳检测技术是一项艰巨的挑战

这项全面的科学研究仔细评估了大多数最先进的异常检测算法。我们从不同领域收集和重新实现了 71 种异常检测算法，并在 976 个时间序列数据集上进行评估。该算法是从不同的算法家族和检测方法中选择的，以表示整个异常检测技术频谱。在本文中，我们对技术及其共性进行了简要的概述；我们评估了它们各自的优点和缺点，因此考虑了有效性、效率和稳健性等因素。我们的实验结果应该简化算法选择问题并打开新的研究方向。

1 异常检测范围

数据序列是数据点的有序序列。数据点基于连续度量来描述一些对象或过程属性，例如温度（例如例如，物理）、质量（例如例如，化学），角度（例如例如，天文学）、位置（例如例如，地质）或速度（例如例如，机械工程）。如果顺序基于时间，则序列通常称为时间序列。无论排序度量如何，数据点的记录通常遵循离散的、等间隔的间隔。出于这个原因，由于大多数时间序列分析算法与参考度量无关，我们交替使用术语数据序列、时间序列和序列。

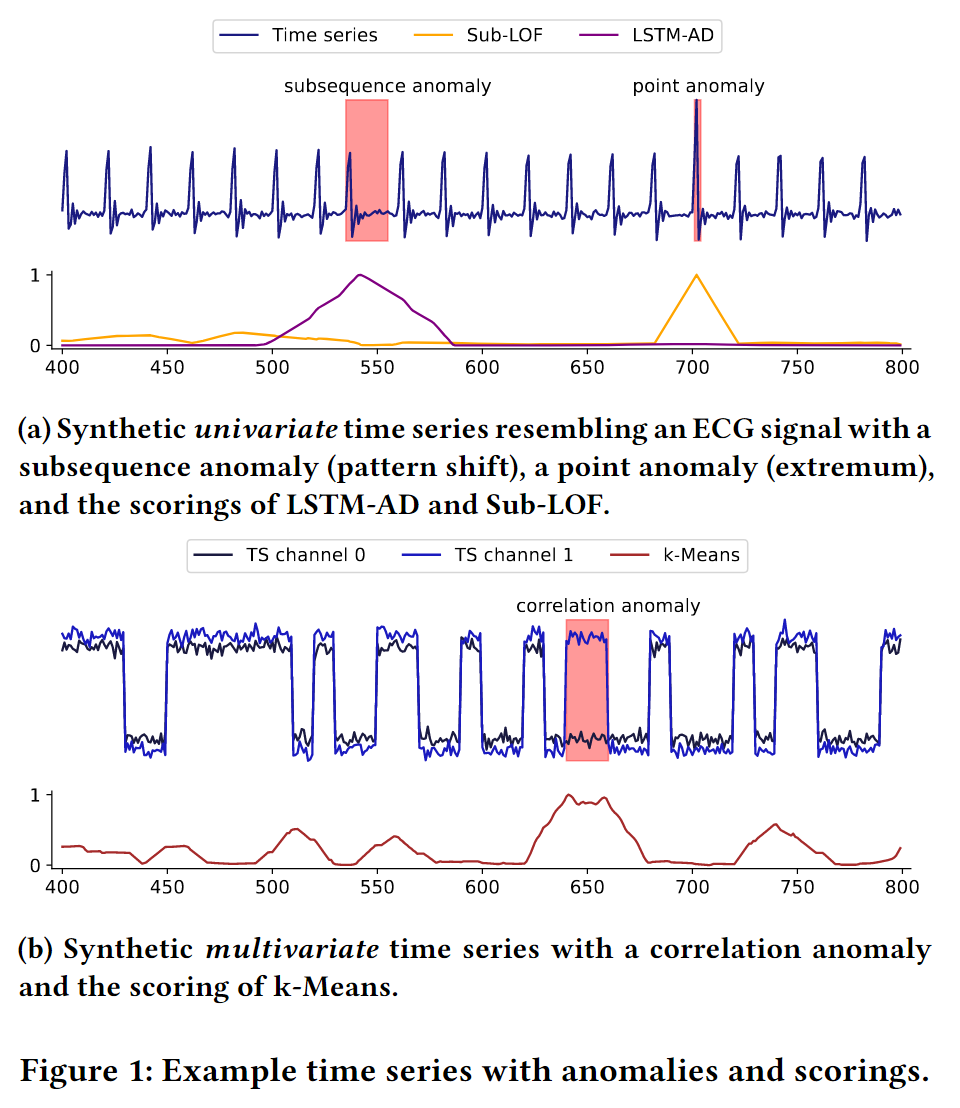
时间序列记录的数据点是一个或多个实值变量。每个变量对时间序列的一个通道进行建模。如果数据点只包含一个变量，则时间序列称为单变量；否则，它是多变量的。图 1 显示了两个时间序列的示例：模拟心电图 (ECG) 信号上的单变量时间序列和具有随机模式跳跃的合成生成的多变量时间序列。此类时间序列中的异常是偏离序列规则模式的某些度量、模型或嵌入的点（例如异常值）或点序列（例如不规则性）。在多变量时间序列中，这些模式偏差可能发生在任何单个通道中，也可能发生在通道的相关性（例如，偏斜）中，如图1b所示。异常子序列可能具有不同的长度，并且它们可能会在同一时间序列中重新出现。根据时间序列的领域，其异常可以描述重要事件，例如心脏病学中的心力衰竭[4]、喷气涡轮机工程中的结构缺陷[145]或地球科学中的生态系统干扰[35]。

不同的异常类型、模式模型和时间序列属性导致了多种不同的异常检测算法的发展，其中存在各种调查[12,20,27,28,29,37,38,53,63]。我们总共收集了 158 篇关于时间序列数据集的异常检测算法的出版物。其中许多遵循非常相似的检测方法，但一般的各种方法非常高，从统计分析、信号处理和数据挖掘到深度学习方法的简单异常值检测。由于所有这些方法都表现出个体的优缺点，因此为给定的异常检测任务选择合适的算法非常困难。例如，图 1a 显示距离方法 Sub-LOF 非常好地检测到点异常，因为它对值幅度和变化幅度很敏感；然而，它无法检测到子序列异常，因为它对点顺序不敏感。相反，LSTM-AD作为一种预测方法学习正常模式，严重依赖于季节性/周期性;因此，它很容易识别异常子序列，但由于对噪声具有鲁棒性，忽略了点异常。

由于目前还没有全面的科学研究来评估时间序列异常检测算法，因此完全不清楚它们的表现如何。r。t。不同的数据集、异常类型和参数设置。考虑到现有的评估（调查 [20, 37] 和单个算法），我们发现它们通常只考虑一小部分相关工作算法，并且它们通常基于琐碎的、精心挑选的、有偏见的、错误标记的、不切实际的或只有少数数据集。出于这个原因，Wu 和 Keogh 甚至声称所有“当前时间序列异常检测基准都是有缺陷的”[147]。

为了创建有意义的评估，我们收集并重新实现了大量71种异常检测算法，这些算法代表了广泛的异常检测家族。对于他们的评估，我们将来自不同领域的 976 个时间序列数据集放在一起，并生成几个具有人工但特别有趣的异常的数据集。本实验研究中使用的算法和数据集的多样性应该为时间序列异常检测的最新技术提供清晰可靠的图景。总之，这项研究做出了以下贡献：

(1) 简短调查：我们提供了 158 个时间序列异常检测技术的分类以及不同算法族的简短描述；我们解释了我们对本次实验评估的算法选择以及算法背后的一般思想。我们提供了最全面的调查并突出了新颖的维度。（第 3 节）

(2) 详尽的评估：我们在 976 个单时间序列数据集上评估 71 个具有代表性的异常检测算法，并在准确性和运行时间方面报告它们的性能；我们分析了不同算法/技术的优缺点，因此考虑了各种时间序列特征。这为算法、数据集和特征提供了最广泛的视图。（第 4 节）

在本文中，我们提供了实用的研究见解（RIs 1 到 14），应该帮助专家为他们的异常检测任务选择最佳算法。我们的研究还显示了时间序列异常检测的最新技术，因此作为研究人员进入该主题的入口点。我们指出了未来研究的潜力，通过这种方式，支持开发现在能够解决特定问题的新算法，利用某些能力，并最终推进异常检测领域。

在此评估中，我们专注于科学发布和/或集成到流行时间序列库中的算法——换句话说，用户实际可用的异常检测方法。因此，这项研究判断具体的实现，只间接判断他们使用的技术和措施。为了公平比较，我们尝试清楚地修改、增强或组合算法和状态，其中需要修改。关于参数化，我们将相同的仔细和系统的努力投入到每个算法中。最后，这可能会导致每个算法的最佳参数配置，但它会导致在实践中代表算法的性能测量，其中用户在其参数化能力上同样受到限制。

2 时间序列和异常

在这项研究中，我们研究了检测时间序列数据中异常子序列的算法。时间序列（或一般数据序列）是一个有序集 T = {T1,T2,.,T} 的 Ô 实值，潜在的多维数据点 푡 ∈ R푡。子序列푡，푡={T，.,T } ⊆ T是长度为|푡 的连续段，T | = T − T + 1 和 | 푥,푡 | ≥ 1。我们的评估假设数据点是等距的，这对于大多数现实世界的时间序列来说是正确的，并且减轻了算法解释具体的连续度量（时间、质量、角度等）；不遵循这个假设的数据序列需要离散化。

异常的具体定义在文献中有所不同。个人、异常数据点通常被称为异常值[2]。给定时间序列数据的顺序特征，将异常数据点分为点、序列和上下文异常[20]，以考虑分类中的长度和上下文信息。当将时间序列细分为固定大小的子序列时（例如例如，通过窗口），各个模式的（ab）正态性可以通过它们与（最近邻）邻居模式 w 的距离来定义。r。t。某些相似性和距离度量。这导致 i。一个。到不和谐的异常概念[70]。因为我们的目标是评估具有不同解释异常行为的异常检测方法，我们使用以下一般定义：

定义 2.1。时间序列异常是一系列数据点 푡，长度 푡 −푡 +1 ≥ 1 偏离 w。r。t。时间序列中频繁模式的一些特征嵌入、模型和/或相似性度量。
时间序列异常检测是在给定的时间序列中标记异常的过程。两个相关的分析任务是时间序列预测[65]和时间序列分类[87]。时间序列预测描述了预测时间序列未来进展的过程；尽管这一活动不是本研究的重点，但许多异常检测方法，如DeepLSTM[31]、Torsk[60]、ARIMA[65]和NumentaHTM[3]，在内部使用时间序列预测，并使用预测值与观测值的偏差来确定异常。相反，时间序列分类描述了将整个时间序列分配给某些类的过程；它通常被用作后处理步骤，将检测到的异常分类为特定领域的类别，但一些异常检测算法，如PS-SVM[85]、SR-CNN[112]、COPOD[80]和NoveltySVR[86]，在内部使用分类技术将时间序列分解分配给预定义的类别。
我们在本研究中研究的异常检测算法提出了不同的嵌入、模型和相似函数。其中一些基于统计分析，其他基于机器学习，其他基于数据挖掘。在本文中，我们旨在通过测量算法在各种（现实世界）场景中的准确性来评估这些技术。对于这种比较，结果需要转换为统一的输出格式。所有异常检测算法最统一的结果格式是数据点的逐点评分。我们将其定义如下：

定义 2.2。时间序列评分 푡 = {푡1, 푡2,., < } 与 푡 ∈ R 是时间序列异常检测算法的结果，该算法为每个数据点 푥 ∈ 푡 分配一个异常分数 푡 ∈ 푡。对于任意两个分数 푡 和 푡 ，必须为真，如果 푡 > 푡 ，则 푡 比 푡 更异常（在它们各自的上下文中）。

我们对各种算法的重新实现将所有输出（分数、置信度、距离等）转换为具有定义 2.2 属性的时间序列评分。对于对整个子序列 푟, 进行评分的算法，我们将子序列分数分配给所有 푡 ∈ 푒, 푡。如果数据点从多个重叠的子序列接收子序列分数，即当它们是重叠子序列的一部分时，我们将这些分数的平均值指定为单个点分数（最大聚合表现更差）。异常分数转换为二进制异常标签（例如g., 0 表示正常，1 表示异常）通过阈值是一个正交的、算法无关的问题，我们在此评估中不考虑。因此，任何将分数转换为二进制标签的阈值都是从评估算法中删除的（如果可能）。
为了评估各种评分，我们使用曲线下面积 (AUC) 度量：接收器操作特征曲线下面积 [57, 19] (AUC-ROC)、Precision-Recall 曲线下面积 [109, 39] (AUC-PR) 和基于范围的精度、基于距离的召回曲线下面积 [131] (AUC-PTRT)。AUC-ROC 和 AUC-PR 已被用于大多数时间序列算法的评估，因此，用于将我们的结果与现有的评估结果联系起来。基于范围的精度 (PT) 和基于距离的召回 (RT) 是最近专门为时间序列异常开发的评估指标 [131]； AUC-PTRT 简单地计算这两个新指标曲线下的面积。通过考虑评分的顺序，它对获得的结果提供了不同的视角。如果存在明显将异常点与评分中的正常点分开的阈值，所有三个指标都分配 1.0 的完美分数，而不管该阈值实际上是什么。

AUC-PR 将精度与召回分数进行对比，而 AUC-ROC 使用假阳性率 (FPR) 而不是精度。数据集中负样本 (N) 的数量对 AUC-PR 的影响高于 AUC-ROC，因为精度是真阳性 (TP) 与所有预测阳性 (PP) 的比率（精度 = ŋ 。较高的 N 引入了更多潜在的误报 (FP)，因此更高的 PP。AUC-ROC 使用的 FPR 是比率 푡 い い。较高的 N 可能反映在 FP 和 N 中。因此，FPR 受到 N 的影响小于精度。适当的度量取决于特定的用例：AUC-ROC 奖励敏感算法，而 AUC-PR 奖励精确的算法。AUC-PTRT 软化了 AUC-PR 非常严格的精确要求，以使度量适应子序列。

3 异常检测技术

本节提供了对我们评估中考虑的现有异常检测算法的广泛但简明的调查。该算法起源于不同的研究领域，属于不同的方法家族。更具体地说，我们发现 (i) 深度学习中的异常检测算法，(ii) 随机学习，(iii) 经典机器学习，(iv) 异常值检测，(v) 统计（回归和预测），(vi) 数据挖掘，以及 (vii) 信号分析。总体而言，我们收集了 158 篇出版物，这些出版物都描述了检测时间序列异常的独特方法。图 2 显示了按研究领域分组的所有收集的出版物。

在我们的实验评估中，我们考虑了 71 种算法的代表性子集，这些算法涵盖了所有类型的方法和方法家族。在图 2 中，71 种考虑的算法以蓝色斜体突出显示。表 1 简要概述了所选算法、它们的属性及其实现。

表 1 由两个基本算法类别构成：算法支持的输入维度（列“D”）及其学习类型（列“L”）。输入维度类别描述了算法是否可以使用变量间依赖关系和相关性（多变量）而不是（单变量）。与一般的异常值/异常检测问题一样，时间序列异常检测算法也可以分为三种类型（cf.[29]）：无监督、监督和半监督。Hodg 和 Austin 在异常值检测方法的调查中分别调用这些类别类型 I、TYPE II 和 TYPE III [63]。无监督(TYPE I)算法在没有先验知识的情况下将异常点与时间序列的正常部分分离(不需要显式训练步骤)。这些算法假设异常子序列可以与正常子序列分离，因为它们 i。a. 频率较低，具有不同的形状和行为，或者源自不同的分布。监督 (TYPE II) 算法对时间序列中的正常和异常行为进行建模，并在它们可用于新时间序列之前需要训练步骤。训练时间序列的所有点必须被标记为正常（通常为 0）或异常（通常为 1）。这些算法学习区分训练时间序列的正常和异常行为。给定一个看不见的测试时间序列，算法可以标记与其异常行为的内部表示相匹配的异常子序列。监督算法受限于它们检测看不见的异常的能力，因此很少用于时间序列中的异常检测。半监督(TYPE III)算法试图只学习训练时间序列的正常行为。这意味着应该在正常时间序列上进行训练以构建正常行为的模型。当应用于测试时间序列时，不符合正常行为的所有子序列都被标记为异常。

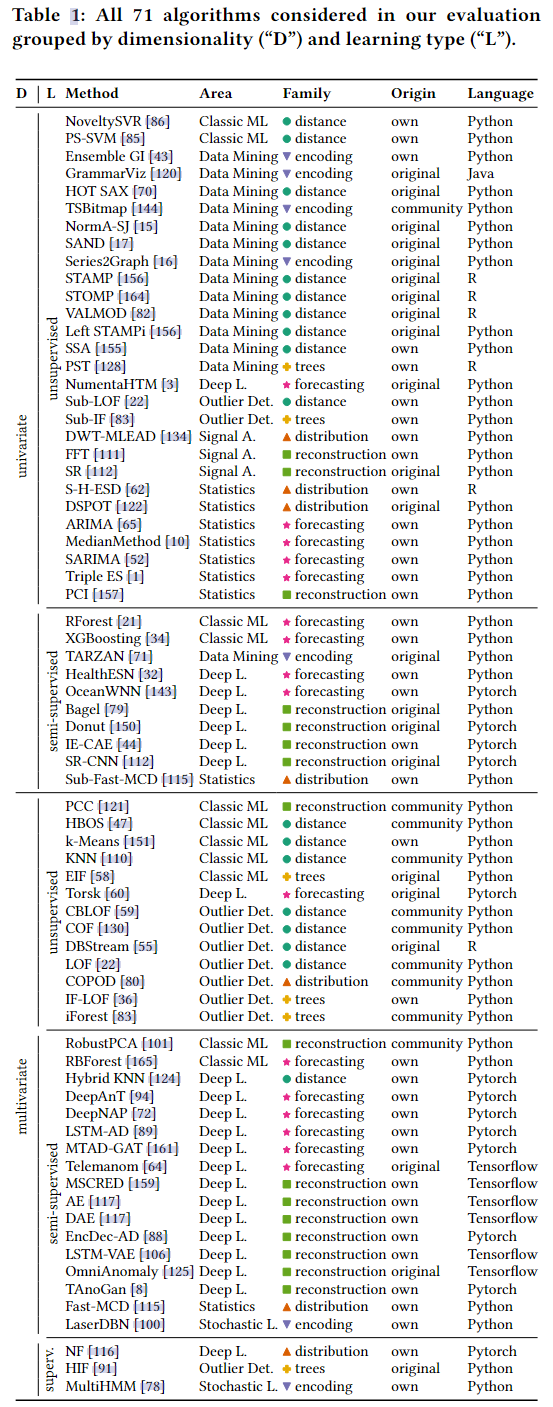
除了输入维度和学习类型类别外，我们还将时间序列异常检测算法分为六种方法家族：（i）预测（第 3.1 节），（ii）重建（第 3.2 节），（iii）距离（第 3.4 节），（iv）编码（第 3.3 节），（v）分布（第 3.5 节）和（vi）树方法（第 3.6 节）。这些方法家族通过确定时间序列内特定点或子序列异常的一般方法来表征算法。以下部分更详细地描述了方法家族，并介绍了本研究中评估的成员算法。
虽然我们没有修改、增强或组合以特定方式发布的算法，但我们将子序列 LOF (Sub-LOF) [22]、子序列隔离森林 (Sub-IF) [83] 和子序列 Fast-MCD (Sub-Fast-MCD) [115] 作为应用于时间序列子序列的异常值检测技术的代表，这在子序列异常检测研究领域中很常见 [9, 15, 17, 119]。实际上，这意味着单变量时间序列不是将这些算法应用于多变量时间序列的单个多维点，而是首先使用滑动窗口将单变量时间序列拆分为固定长度的子序列，然后将该算法应用于这些子序列。根据我们的行业合作伙伴的要求并涵盖可能最广泛的方法，我们还包括随机森林回归器 (RForest) [21]、随机森林 (RBForest) [165] 和 XGBoosting [34] 算法，这些算法是常见的半监督机器学习技术应用于子序列以进行异常检测。

3.1预测方法

预测方法（符号：）使用（连续）学习模型根据当前上下文窗口预测许多时间步长。预测数据点的值仅取决于前一个上下文窗口中的时间序列数据点和先前学习的模型。然后将预测点与原始时间序列中的观测值进行比较，以确定观测值的异常程度。大多数预测方法使用步幅为 1 的滑动窗口来构建上下文窗口并一次预测单个点。该家族中的方法在他们使用的预测模型类型上有所不同（即例如，正常行为模型的类型），以他们构建这个模型的方式（即e.，学习方法)和异常分数的计算度量(即例如，预测值和观测值的距离度量）。我们在评估中考虑的类别的代表是：AD-LTI [148]、ARIMA [65]、DeepAnT [94]、DeepNAP [72]、HealthESN [32]、LSTMAD [89]、MedianMethod [10]、MTAD-GAT [161]、NumentaHTM [3]、新颖性SVR [86]、OceanWNN [143]、RBForest [165]、RForest [21]、SARIMA [52]、Telemanom [64]、Torsk [60]、Triple ES [1] 和 XGBoosting [34]。

通常，预测方法以半监督方式进行训练：没有异常的训练时间序列用于学习数据的正态模型。与测试时间序列中的这种正常预期行为的偏差，即例如，观察到的数据点和预测数据点存在显着差异，被认为是异常的。这适用于 RBForest、RForest、OceanWNN、XGBoosting、AD-LTI、DeepAnT、DeepNAP、HealthESN、LSTM-AD（可以预测多个点）、MTAD-GAT 和 Telemanom。然而，NumentaHTM、新颖性SVR、Torsk（也可以预测多个点），ARIMA 和 SARIMA 使用一些初始点（无监督）直接在测试数据集上构建它们的正常模型。对于这些初始点，这些方法假设正态性，不计算异常分数。该模型定期重建以适应数据的变化。在 MedianMethod 和 Triple ES 中，模型更新被置于一个极端。两种算法从每个上下文窗口重建整个正常模型：MedianMethod 使用上下文窗口的中值作为预测，而 Triple ES 将三重指数平滑模型拟合到每个上下文窗口以预测一个后续点。

3.2重建方法

重建方法（符号：）通过对（低维）潜在空间中正常训练时间序列的子序列进行编码来构建正常行为模型。为了检测测试时间序列中的异常，从潜在空间重建来自测试序列的子序列，然后将重建的子序列的值与原始的观察到的序列值进行比较。重建过程的输入是训练窗口（通常使用步幅为 1 的滑动窗口创建），它为模型提供时间上下文。由于该模型仅基于正常数据（半监督）构建，因此模型无法重建测试序列中的异常子序列。因此，异常分数可以通过原始子序列和重构子序列之间的差异来计算。我们评估中该类别的代表性是：自动编码器 (AE) [117]、Bagel [79]、去噪自动编码器 (DAE) [117]、Donut [150]、EncDec-AD [88]、FFT [111]、图像嵌入 CAE (IE-CAE) [44]、LSTM-VAE [106]、MSCRED [159]、OmniAnomaly [125]、PCI [157]、PCC [121]、RobustPCA [101]、光谱残差 (SR) [112]、SR-CNN [112] 和 TAnoGan [8]。

3.3编码方法

编码方法 (symbol: ) 与重建方法相似，因为它们还对低维潜在空间中的时间序列子序列进行编码。然而，他们没有尝试从潜在空间重建子序列，而是直接从潜在空间表示计算异常分数。更具体地说，异常分数归因于对应于潜在空间中的编码子序列的点。在此评估中，我们考虑以下类别的代表：Ensemble GI [43]、GrammarViz [120]、LaserDBN [100]、MultiHMM [78]、PST [128]、Series2Graph [16]、TARZAN [71] 和 TSBitmap [144]。GrammarViz 及其后继者 Ensemble GI 将子序列离散化，然后推断分层语法规则;这两种算法都认为难以压缩的子序列（语法规则覆盖率低）是异常的。类似地，TSBitmap 将离散化子序列编码为保留子序列频率的位图；然后使用前导窗口和滞后窗口位图之间的距离作为异常分数。TARZAN 还编码离散化子序列的频率，但它对训练和测试时间序列（半监督）使用后缀树；子序列对观察频率的预期频率（来自训练）之间的差异用作异常分数。LaserDBN、PST 和 MultiHMM 构建概率模型，并使用子序列的对数似然作为其异常分数；而 MultiHMM 从正常的训练时间序列（半监督）构建模型，LaserDBN 和 PST 只考虑测试时间序列。Series2Graph 将测试时间序列的子序列转换为低维空间，该方法构建有向循环图。图的边表示子序列组之间的转换。时间序列遍历一条边的频率越高，其得分越高。因此，得分较低的边更异常。

3.4距离方法

距离方法（符号：）使用专门的距离度量来比较时间序列的点或子序列。与具有正常行为的子序列相比，异常子序列预计与其他子序列的距离更大。对于距离计算，该家族中的算法可以取所有其他子序列，只有一些最近邻，或者某些聚类质心作为距离参考点。一些方法在计算距离之前将子序列映射到多维空间。基于聚类的距离方法将相似的子序列聚集在一起，然后计算到密集区域的距离。此类别中的大多数方法通过滑动窗口创建子序列，该滑动窗口在测试时间序列上步幅为 1。基于距离的方法通常不需要训练数据，因此是无监督的。我们评估中该类别的代表性是：CBLOF [59]、COF [130]、DBStream [55]、HOT SAX [70]、Hybrid KNN [124]、k-Means [151]、KNN [110]、LOF [22]、NormA-SJ [15]、PhaseSpaceSVM (PS-SVM) [85]、SAND [17]、SSA [155]、STAMP [156]、STOMP [164]、Sub-LOF [22]、VALMOD [82] 和 Left STAMPi [156]。
最近邻方法通过计算点 (KNN, COF, LOF) 或子序列 (STAMP, STOMP, VALMOD, 左 STAMPi, Sub-LOF, HOT SAX, Hybrid KNN) 到其最近邻居的距离来确定异常分数。不常见的子序列与其邻居的距离很大，因此被评分为异常。这个组的特定子类(STAMP, STOMP, VALMOD, Left STAMPi)有效地计算矩阵轮廓，记录每个子序列到其最近的非自邻居的距离[156,164]。DBStream 和 k-Means 对子序列进行聚类，然后使用子序列与其对应的聚类质心之间的距离作为异常分数。类似地，CBLOF 使用多维点而不是子序列进行聚类。NormA-SJ、SAND 和 SSA 构建了与子序列进行比较的正常行为的参考模型。子序列和参考模型之间的距离用作异常分数。PS-SVM 将单类 SVM 拟合到子序列的转换表示中，并使用到决策边界的逆距离作为异常分数。该家族中唯一的半监督方法是混合KNN；它需要没有异常的正常训练数据来构建与新子序列进行比较的正常模型。

3.5分布方法

分布方法（符号：）估计数据的分布或将分布模型拟合到数据中。分布是在数据点或通过窗口获得的子序列上计算的。尽管点和子序列的相似性可能是分布拟合的一个因素（非常相似的模式被视为相等），但异常是通过频率来判断的，而不是该算法家族中的距离。异常分数通常使用点或子序列 w 的概率、可能性或距离来衡量。r。t。先前计算的分布。一般来说，这是一种无监督方法，因为异常可以在分布的极端/尾部找到。在半监督情况下，分布是在仅包含正常行为的训练时间序列上估计的，然后根据先前学习的分布检查测试时间序列的点或子序列。我们评估中分布方法的代表性为：COPOD [80]、DWT-MLEAD [134]、Fast-MCD [115]、HBOS [47]、归一化流 (NF) [116]、S-H-ESD [62]、DSPOT [122] 和 Sub-Fast-MCD [115]。
DWT-MLEAD、Fast-MCD 和 Sub-Fast-MCD 估计时间序列上的高斯分布。之后，点或子序列的异常是通过它们与分布平均值的距离来衡量的。这些方法的不同之处在于 DWTMLEAD 使用离散小波变换 (DWT) 作为预处理步骤，子序列的对数似然作为异常分数；另一方面，Fast-MCD 和 Sub-Fast-MCD 将分数计算为点 (Fast-MCD) 或子序列 (Sub-Fast-MCD) 与正常训练时间序列的估计高斯分布（半监督）之间的马氏距离。另一种算法HBOS在直方图的帮助下估计子序列的通用概率分布；然后，它使用子序列的直方图箱的逆密度作为异常分数。COPOD 算法构建了一个经验多维累积分布函数（copula）来估计点的尾部概率；然后将这些尾部概率转化为异常分数。S-H-ESD 是一个点异常检测器，首先执行 STL 时间序列分解，然后在残差上应用 Gubbs 测试，该测试假设高斯分布来标记异常值点。另一个点异常检测器DSPOT估计时间序列极值的广义帕累托分布，并对分布尾部应用阈值来标记异常点。最后，NF 是一种有监督的序列异常检测方法，它使用神经网络将任意先验分布转换为高斯分布；然后它将落入分布尾部的子序列标记为异常。

3.6隔离树方法

隔离树方法 (symbol:
) 构建了一个随机树的集合，它对测试时间序列的样本（点或子序列）进行分区。对于树构造，该方法递归地选择随机特征和随机分裂值作为树节点，最终分离树叶子中的样本。隔离样本所需的拆分数量是由集合中所有随机树的平均路径长度描述的度量。由于异常样本比正常样本更容易分离，因此它们平均更接近树根并且具有明显更短的路径。出于这个原因，路径长度是样本正态性的特征，因此它们的倒数值转化为异常分数。我们评估中该类别的代表性是：扩展隔离森林 (EIF) [58]、混合隔离论坛 (HIF) [91]、隔离森林 - 局部异常值因子 (IF-LOF) [36]、隔离森林 (iForest) [83] 和 Sub-IF [83]。
上述一般隔离树方法，这也是该家族中的所有算法都基于的方法，是 iForest 算法。这种方法的监督变体是 EIF 和 HIF。Sub-IF算法是子序列异常检测的扩展，即例如，可以处理序列而不是点的算法，IF-LOF 是 iForest [83] 和 LOF [22] 的组合。

4 实验评估

对于我们的实验评估，我们在 976 个真实世界和合成数据集（第 4.1.2 节）上执行 71 个算法（第 4.1.1 节）。我们在一组标记良好的合成数据集上全局优化所有算法的参数，以便实验对每个算法使用可能的最佳配置（第 4.1.3 节）。在本节中，我们最终对算法的质量（第 4.2 节）和运行时行为（第 4.3 节）进行了详尽的评估。
我们强调，该评估通过正确发布的实现来比较时间序列异常检测算法，并从结果中得出关于不同概念和家庭的结论。对所有概念进行详尽的评估（矩阵配置文件与自动编码器与树与树的比较。) 在所有可能的实现中在技术上是不可能的。因此，如果算法在我们的评估中表现出较差的性能，这并不一定意味着其概念很差。然而，糟糕的性能表明，在实践中，使用特定方法获得良好的结果是困难的。

4.1环境和设置

在这项研究中，我们开发了一个名为 TimeEval1 的评估工具，该工具管理众多评估任务的执行。评估任务是分析一个数据集的算法。TimeEval 是一个 Python 3.8 程序，可以自动调度、执行和分析计算集群上一组预定义的评估任务。它测量并计算我们在本节中报告的所有指标、状态代码和执行时间。由于 TimeEval 在单独的 Docker 容器中运行算法，因此算法不限于特定的编程语言或版本，TimeEval 可以将评估任务分布在计算机集群上。我们在配备 Intel Xeon E5-2630 v4 CPU（2.2 GHz 的 10 个内核）的 14 个服务器集群上进行了实验。每个 Docker 容器，因此每个算法都被限制在一个 CPU 内核和一个 3 元内存。因此，每个节点可以同时运行 10 个任务。整个集群可以并行执行 140 个评估任务。我们不使用 GPU——既不用于训练也不用于测试。

所有实验都分别定义了 2 ℎ 的训练和执行时间的时间限制，内存限制为 3𝐺𝐵。我们对(半)监督算法采用早期停止和模型检查点，该算法需要多次迭代训练时间序列，即e.每个时期一次。每个算法最多获得 2 小时以适应训练数据，然后使用最佳模型对测试数据进行异常检测。如果算法无法在时间限制内完成单个 epoch，或者需要超过 2 小时来检测测试时间序列上的异常，我们认为它是超时的。Fast-MCD、RForest、XGBoosting、HealthESN、HIF、LaserDBN、MultiHMM、RBForest、RobustPCA、Sub-Fast-MCD 和 TARZAN 是（半）监督并且没有迭代训练方法。因此，模型检查点策略不适用于这些算法。
4.1.1 算法。在我们在本次评估中考虑的 71 种算法中，我们收集了 22 种作者实现（原始），找到了 10 种可靠的社区实现（社区），如果没有获得实现（拥有），则重新实现 39 种算法（cf.表1）。一个特殊的 TimeEval 包装器添加了所需的接口，并将算法输出转换为时间序列评分。从 71 种实现的算法中，由于命中内存或时间限制，5 种算法无法处理单个数据集（43, 52, 86, 159, 161]。其他五种算法在任何数据集上都没有产生单一合理的结果 [106, 115, 115, 117, 117]。因为我们无法从提供的材料中解决问题（如果有），所以我们从我们的分析中排除了这 10 种算法。
4.1.2 数据集。在这项研究中，我们从 24 个集合中收集了 1,354 个数据集。表 2 列出了它们的时间序列的集合、它们的基数和维度。由于收集的数据集中异常标签的不可靠性[147]，我们开发了Good时间序列异常生成器(GutenTAG)，并生成了另一个194个具有大量标记良好的异常的时间序列。

生成的时间序列有五种基本类型（正弦波、心电图、随机游走、圆柱钟漏斗和多项式），具有不同的长度、方差、振幅、频率和维度。注入异常的选择涵盖九种不同的类型（振幅、极值、频率、平均值、模式、模式偏移、平台、趋势和方差），这对于分析某些检测能力特别有趣。此外，定义明确且可靠的标签可实现算法的稳定参数化。
从 1,354 个收集的数据集中，我们删除了 (a) 没有异常的所有时间序列，因为没有找到任何异常； (b) 有 > 0.1，因为有超过 10% 的异常点的对象是异常很少见的假设（主要是 SSA、占用和道奇）； © 不能被至少 50% 算法处理（通常是由于它们的大小和严格的内存和时间限制），因为这扭曲了我们的分析结果（主要是 Exathlon、IOPS、Kitsune 和 LTDB）； (d) 不能通过单个算法以至少 0.8 的 AUC-ROC 分数处理，因为这表明标签质量很差（主要是 MITDB、SVDB 和 Daphnet）。NAB 集合包含一些不符合我们一些过滤器的数据集，但无论如何我们将它们包括在内，以了解算法如何对这些数据集做出反应。我们还包括来自 Exathlon 和 IOPS 的四个随机选择的数据集，尽管它们的大小很大，但要将评估中的至少几个大时间序列捕获为非常有效的方法的食物。过滤后，剩下 976 个时间序列数据集（cf.表 2）。
4.1.3参数化。为了比较算法的最佳可能配置，我们进行了系统（超）参数调整过程。由于对 192 个参数、976 个数据集和三个评估指标的完整参数网格搜索显然是不可行的（在实践中运行是不现实的），我们假设参数独立性并分别优化每个参数以获得所有合成 GutenTAG 数据集上的最佳平均 AUC-ROC 分数。然后使用最佳参数值（参见可用性页面）进行整个评估。更具体地说，调整执行如下：
(1)参数初始化：我们首先从算法的出版物或参考实现提供的默认值推导出初始设置；如果没有提供设置，我们通过对几个数据集进行简要测试来手动设置合理的值。
(2) 参数分类：我们将所有单独的 192 个参数分为四类：固定（99）、相关（12）、共享（11）和优化（70）。固定参数是默认参数，没有明显的替代方案，仅影响运行时性能的参数，或具有非常明确的默认建议的参数。相关参数是那些最佳值取决于时间序列属性的参数，因此它们无法全局定义。例如，最佳窗口大小取决于处理数据集的周期大小或主导频率。因此，对于相关参数，我们优化了用于从时间序列元数据中动态计算它们的启发式方法。共享参数是出现在具有相同函数的多个算法中的参数。这些参数可以针对它们出现的所有算法联合优化，从而节省时间和增加公平性。优化参数是每个算法都需要优化的所有剩余参数。
(3) 参数限制：我们为每个非固定参数定义了一个搜索空间（基于默认值、人类专业知识和临时测试），这是该参数（或启发式）可以采用的特定值范围。对于数值，我们从这个范围中抽取 5 个等距样本（包括默认值）；对于分类和布尔值，我们测试了所有可能的设置。
(4) 自动优化：我们设置 TimeEval 来测试每个先前确定的设置中的所有参数。对于在某些数据集上花费的时间异常长的算法，我们减少了这些数据集的大小以进行参数搜索。然后将具有最佳平均 AUC-ROC 分数的设置提升到默认参数。

4.2结果质量

在本节中，我们首先分析所有实现算法在所有数据集的有效性（第 4.2.1 节）。然后，我们研究了我们的结果和实现的可靠性（第 4.2.2 节）。最后，我们评估了特定异常类型和数据集特征的整体性能（第 4.2.3 节）。
4.2.1 AUC-ROC、AUC-PR 和 AUC-PTRT。表 3 提供了我们所有实验结果的全面定性性能概述。该表列出了所有 61 种算法，这些算法按其输入维度和学习类型分组。表列 TL、OOM 和 ERR 分别显示了实验中超时、内存不足和其他错误的百分比。在他们的组中，算法按其在所有数据集上的平均 AUC-ROC 分数降序排列。右侧的其余列包含每个算法（行）和特定质量度量（列）的框图。我们报告了所有数据集的 AUC-ROC、AUC-PR 和 AUC-PTRT 分数，此外，AUC-ROC 分数仅在我们综合生成的 GutenTAG 数据集上聚合。
61种算法中有39种以无监督的方式检测异常。19 种算法是半监督的，因此必须事先在没有异常的情况下对数据进行训练。(RI 1) 尽管在训练期间使用额外的信息（正常点和异常点的标签）进行监督算法，但与半监督甚至无监督方法相比，它们并没有取得更好的结果。一个例外是 NF 算法，它实现了出色的检测率，尽管只有 34% 的数据集；对于大多数数据集，它要么运行超时，要么错误，这使得报告的结果不是很可靠（cf.4.2.2 节）。除了它们的性能较弱（在本实验中），监督算法在实践中并不受欢迎（158 种方法中只有 7 种是有监督的），很可能是因为在现实世界的场景中通常事先不知道异常。然而，由于有监督的检测方法很容易转化为多变量数据，我们没有发现任何仅限于单变量数据的监督算法。
多变量和单变量算法分数的比较表明，平均而言，单变量算法的表现略好。对于这种比较，我们需要考虑多变量算法在所有时间序列上运行，而单变量算法只处理单变量时间序列。有人可能会得出结论，多元时间序列更难分析，但多变量算法在单变量数据 w 上表现更差 6%。r。t。AUC-ROC 高于我们评估中的多变量数据。因此，我们得出结论，(RI 2) 当前可用算法集中没有一刀切的解决方案：需要一种多变量算法来检测多变量异常（例如例如，序列相关性的异常），但单变量算法更适合单变量数据。

一些算法的训练和/或执行都需要很长时间，或者消耗大量内存，这导致它们超过我们的资源限制：例如，NF、HealthESN、EncDec-AD 和 TAnoGan 在时间限制和 COF、LSTM-AD 和 EncDec-AD 在 20% 以上的实验中耗尽内存。由于多变量数据和算法的复杂性较高，多变量算法经常会出现这些超时和内存错误。具有高错误率的算法实现，例如 S-H-ESD、DBStream 和 MultiHMM，通常失败，因为它们无法处理某些输入特征（例如g.、值平台）或做出不泛化的假设；错误还表明我们无法解决的技术缺陷。一般来说，较高的错误率并不反映算法的性能，因为我们看到两种好的不稳定实现（例如例如，NF）和坏（例如g., S-H-ESD) 分数。(RI 3)尽管我们对每个实现进行了强有力的投资，但相对较高的总体误差敏感性表明，每个实用的算法部署都需要仔细的测试;只有少数实现，如DWT-MLEAD、KNN和Sub-LOF，实际上似乎既健壮又有效。

在比较不同质量指标的结果时，我们观察到 AUC-ROC 和 AUC-PR 分数的排名由于评分重点不同而明显偏离（参见第 2 节）。原因是一些算法标记了异常部分的开始和结束，而另一些算法则标记了整个部分;大多数算法还将向异常的过渡标记为异常，而预测方法倾向于在异常实际开始之前标记异常。例如，DeepAnT 在 AUC-ROC 中比在 AUC-PR 中强得多，而 DBStream 是 AUC-PR 中最强的方法，但在 AUC-ROC 中只是平庸。（RI 4）因此，最相关的评分指标取决于用例以及预期结果所指示的内容。我们在表 3 中提供了所有三个指标的分数以供参考，并在所有其他图表中仅报告 AUC-ROC 分数。

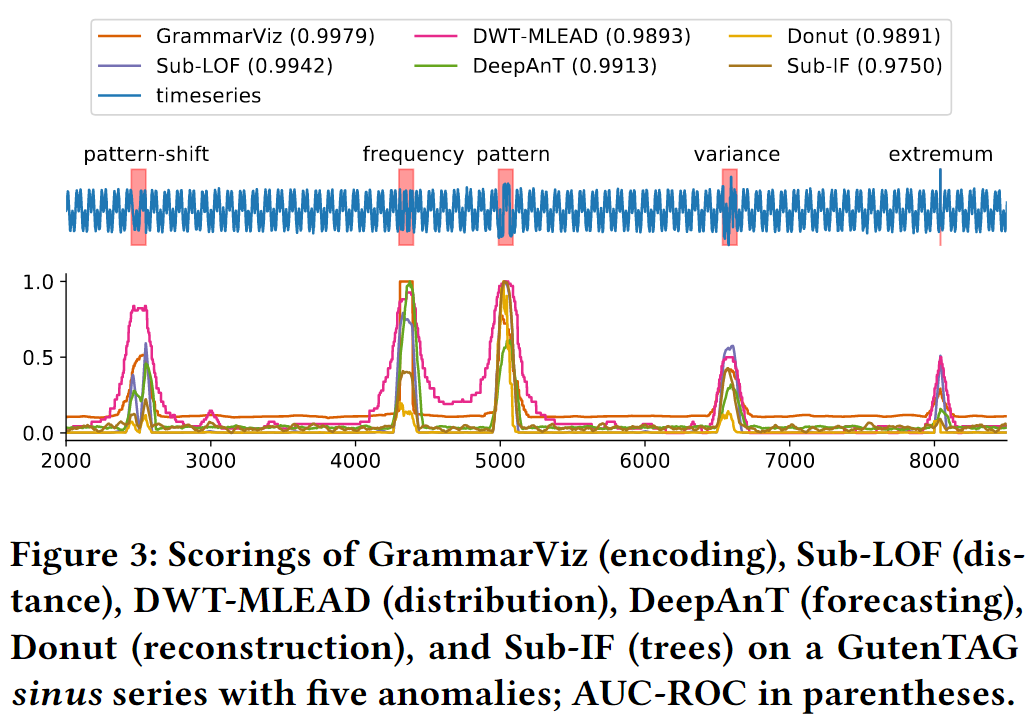
表 3 中的结果进一步表明，仅在 GutenTAG 数据集上进行实验的平均 AUC-ROC 分数高于所有数据集的平均 AUC-ROC 分数；特别是，AUC-ROC 分数方差平均较低。这部分是因为算法已经针对这些数据集进行了优化，这表明需要参数调整。然而，改进（尽管参数计数不同）的清晰度也表明，现实世界的数据集要么更难，要么它们的标记质量更差。因此，我们遵循 [147] 的建议，并为受控数据提供结果以进行性能比较。与我们的一般观察相反，一些异常值检测算法，例如 MedianMethod，实际上在所有数据集上都表现得更好，这是因为现实世界数据中极值异常的比例高于生成的数据，并且它们在这方面表现出色。对于这两种聚合类型，监督算法的结果是相同的，因为收集的数据不包括具有适当标签的时间序列进行监督训练。

表 3 中的评分让我们得出结论，利用简单子序列时间序列聚类的 k-Means 是一种非常有效的多元方法，其性能与距离族的其他代表相似。这令人惊讶，因为先前的研究表明子序列时间序列聚类会产生无意义的聚类中心（通常是正弦信号）[81]。[81]的作者声称，类似于NormA-SJ中使用的主题更准确地捕获了真实的聚类质心，但我们的实验无法证实这实际上有利于异常检测。
图 3 显示了具有不同类型异常的时间序列的 6 个 AUC-ROC 取景。从每个异常检测系列中，我们选择了一个有趣的代表性来证明某些算法优势：GrammarViz（编码）在频率和模式异常检测方面特别强； Sub-LOF（距离）特别精确地标记了模式变化，总体上效果很好； DWT-MLEAD（分布）也非常好地发现所有异常，但它会在异常部分周围的明显宽区域产生高分； DeepAnT（预测）特别检测到模式偏移和频率，作为一种预测方法，其分数总是比所有其他分数高一点； Donut（重建）显然对模式非常敏感，但对幅度不敏感，这就是为什么模式异常在其分数中占主导地位； Sub-IF（树）对模式异常特别敏感，并且在点异常和模式偏移方面遇到了一点。
(RI 5) 我们在不同数据集的实验结果表明，总体而言，每个异常检测家族都是有效的，没有明显的赢家。此外，没有一个单一的算法获得了完美的分数，为未来的工作留下了很大的空间。
4.2.2 结果的可靠性。图 4 将算法的平均 AUC-ROC 分数与其成功处理数据集的百分比联系起来。因此，点的 y 坐标表示点的 AUC-ROC 分数的可靠性。该算法由它们的家族进行颜色编码，最相关的点被标记。
大多数算法 (87%) 已经成功地处理了超过 70% 的数据集，许多算法 (35%) 甚至处理了超过 99% 的数据集。因此，绝大多数报告的质量测量都是可靠的。例如，DWT-MLEAD 的平均 AUC-ROC 得分为 0.83，可靠性为 100%，并且很可能在其他数据集上表现良好。相反，RobustPCA 的平均 AUC-ROC 分数仅为 0.54，可靠性为 100%，因此，很可能在其他数据集上的表现也很差。
只有 8 种算法的可靠性低于 52%，其中 MultiHMM、S-H-ESD 和 TAnoGan 表现不佳，DBStream 和 EncDec-AD 表现平庸，HealthESN、NF 和 LSTM-AD 表现很大。因此，定性表征并不是特别有代表性的，但表现出显着的设置和运行时困难：MultiHMM、S-H-ESD 和 DBStream 遇到了许多我们无法修复的内部错误； NF、HealthESN、EncDec-AD 和 TAnoGan 在 4 ℎ 时间限制下挣扎； LSTM-AD 经常超过 3 万亿内存限制。
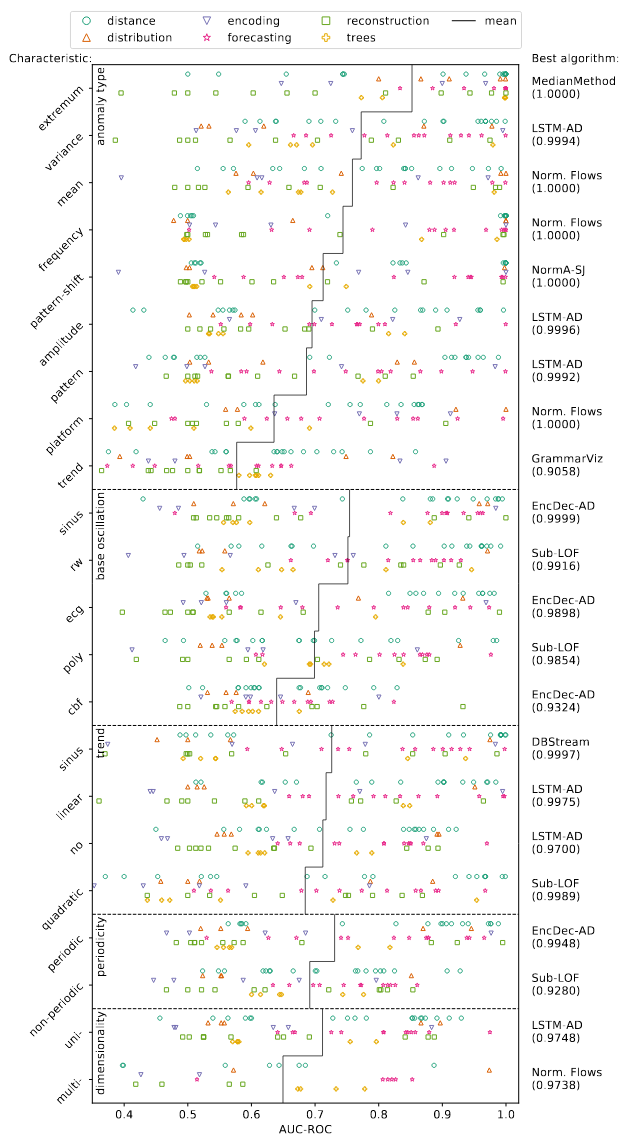图 5：按数据集特征（异常类型、基本振荡、趋势、周期性）分组的质量结果，重点是算法家族。

4.2.3异常类型和数据集特征。我们的数据生成工具 GutenTAG2 生成具有非常特定特征的时间序列（异常类型、基本振荡、趋势、周期性和维度），我们可以使用这些时间序列进行深刻的分析。图 5 显示了按这些特征分组的所有 61 个算法的平均 AUC-ROC 分数：图中的每个点代表一个算法，每一行代表一个特定的特征。为了更好地可读性，每一行都细分为六个颜色编码的子行2有关更详细的描述，请参阅 https://github.com/HPI-Information-Systems/gutentag 上的 GutenTAG 文档。 - 每种方法系列一个。每行中的黑色垂直标记线标记特定特征的所有算法的平均 AUC-ROC 分数，因此特定特征（在生成的时间序列中）的整体性能。我们为每个数据特征注释性能最佳的算法（最高平均 AUC-ROC 分数；最小标准偏差作为平局打破者）。

考虑到异常类型，(RI 6) 极值似乎是最简单的异常（平均AUC-ROC 得分高于 0.8）和（RI 7）趋势最难的异常（平均AUC-ROC 分数低于 0.6）。对于极值异常，我们发现基于树的算法和点异常检测器表现得非常好；对于趋势异常，只有少数编码、距离和预测方法提供了可接受的结果。(RI 8) 频率和模式移位异常清楚地将算法分为（主要是距离和预测）和不能（主要是重建和树）检测到的算法分开。
基本振荡组表明，周期性正弦波中的异常最容易检测，而在混沌圆柱贝尔漏斗 (CBF) 基振荡中，相同类型的异常最难检测。(RI 9)由于混沌时间序列缺乏结构，大多数算法很难找到合适的正常行为表示，也不能完全区分正常和异常子序列。该算法在非周期随机游走 (RW) 时间序列上达到了 0.75 的可疑高平均 AUC-ROC 分数，因为这些序列不包含相对难以找到的模式和模式转移异常——在非周期数据上，无法表示此类异常。然而，窦和心电图的比较表明，越来越复杂的模式也增加了异常检测的难度。
图 5 显示趋势确实对单个算法有影响（有时是正面的，有时是负面的），但所有算法的平均性能对简单趋势惊人地稳健。只有二次趋势似乎会使检测复杂化一点。对于基于距离的算法，趋势是最轻微的问题（如果不是优势）。
(RI 10)周期时间序列上的异常比非周期时间序列更容易检测。尽管平均值仅相差 0.03，但与非周期时间序列（两种算法）相比，更多的算法在周期时间序列（16 种算法）上达到高于 0.90 的分数。如前所述，周期性时间序列还包含更困难的异常，以便在此比较中它们的分数处于不利地位。
我们的测量表明，单变量时间序列的异常检测平均比多变量时间序列更容易。直接比较产生了 0.06 的平均 AUC-ROC 分数。这种效果在我们生成的数据集上尤为明显，因为它们的大部分异常仅存在于单个通道中，这使得它们更难与噪声区分开来。
(RI 11) 总之，大多数重建方法产生的 AUC-ROC 分数相当差（~ 0.5），并且该组中只有一些算法，即例如，EncDec-AD 和 Donut 可以很好地检测所有特征的异常；相反，预测和距离算法产生了特别好的结果，其中许多代表，例如 DeepAnT 和 Sub-LOF，在几乎所有特征中表现最好的算法之一；最后，距离算法在方差异常上表现良好。

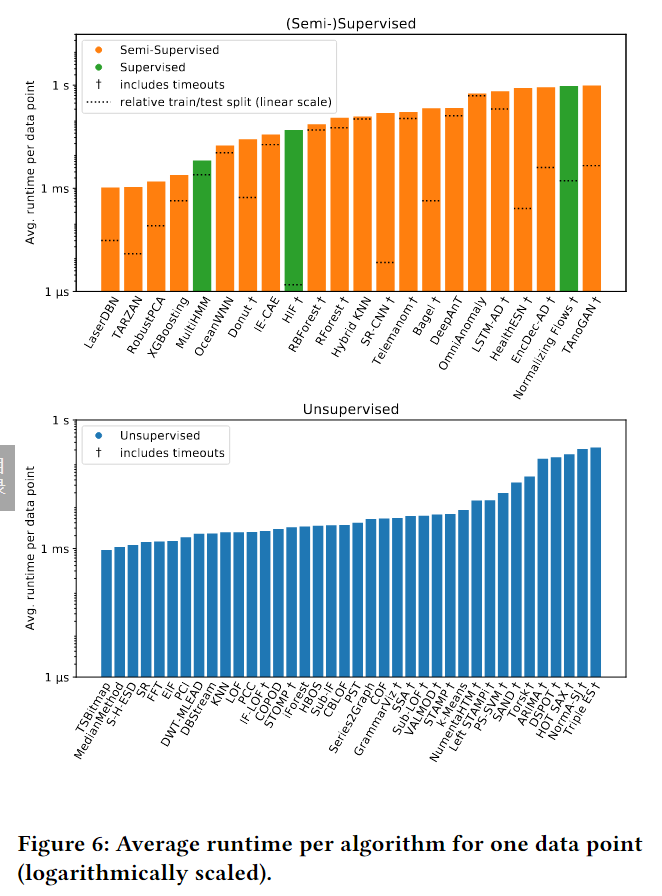
4.3运行时和内存

在最后的实验中，我们测量了单变量时间序列上所有算法的运行时间，并通过相应时间序列的长度对运行时间进行归一化。图 6 显示了每个算法对一个时间序列数据点的平均测量运行时间。绘制的时间涵盖训练和测试时间，时间限制为 2 ℎ。因此，如果（半）监督算法的训练在极限之前不收敛并且它们在测试期间超时，则每个时间序列最多可以占用 4 ℎ。超过时间限制的算法执行被认为是运行时间等于时间限制。如果发生这种情况至少一次算法，则用 † 标记以表明其真实运行时间可能比图中所列长。错误算法执行被排除在考虑之外，因为我们无法测量任何运行时。

(RI 12) 大多数监督和半监督算法在我们的评估中是最慢的算法之一，对于一个数据点，平均需要 255 英尺，这主要是由于它们的训练时间很长。这一观察结果证实了相关工作中得出了类似的结论[67]。然而，有（半）监督方法，例如 XGBoosting、RobustPCA、TARZAN 和 LaserDBN，它们与无监督方法的运行时性能很好地竞争（每个数据点 < 2.5 分）。我们还发现无监督算法，例如 Triple ES、NormA-SJ、HOT SAX、DSPOT 和 ARIMA，它们花费了异常长（每个数据点 125 英尺）。

因为每种方法都计算/学习一些模型来解决任务，所以性能不一定与学习类型相关联。(RI 13) 总体而言，最快的算法和最慢的算法都没有提供质量良好的结果（cf.表 3）。在我们的实验中具有明显最佳成本/效益比的算法是DWT-MLEAD，平均AUC-ROC得分为83%，每个数据点的出色运行时间为2.2‰。
(RI 14) 只有少数实现实际上与我们的 3 谜内存限制作斗争。例如，LSTM-AD 和 EncDec-AD 是深度学习方法，它天生需要比其他方法更多的内存，因此分别超过了 50% 和 26% 的实验的限制。无监督 COF 算法在所有实验中也超过了 24% 的限制。它的内存效率相对较低，但能够分析多变量数据，而其他内存占用较低的无监督方法则不能。

5 讨论

与相关工作 [67] 一致，我们发现深度学习方法（但）具有竞争力，尽管它们对训练数据的处理工作量更高。我们还可以确认“简单方法产生的性能几乎与更复杂的方法一样好”[56]。尽管如此，没有一个算法显然表现最好。我们强调了几种具有特定优势的算法，但整体性能结果需要以下三个领域的进一步研究：
灵活性：没有算法（或算法家族）明显支配所有其他方法并解决所有异常检测设置。为了推进异常检测领域，我们提出了对整体和混合异常检测系统的进一步研究，该系统结合了现有的优势，用于检测具有任意特征的时间序列中更多样化的异常。
可靠性：尽管我们尽最大努力，但只有少数算法可以处理所有没有错误和常见时间和内存限制的时间序列。因此，我们强调进一步研究时间序列异常检测算法的鲁棒性和可扩展性的重要性。
简单性：本研究的大多数异常检测算法对其参数设置非常敏感，平均需要七个设置。更糟糕的是，大多数实际用例没有算法配置的训练数据。出于这个原因，非常需要进一步研究自动配置和自调优算法。

致谢

我们感谢我们社区的所有成员发布或提供他们的数据和源代码，如果没有这些成员，这项工作就不可能实现。我们感谢非常多的 Grit Fessel、Ulrike Herwig、Siddeshkanth Logonathan、David Matuschek、Rohan Saawahn 和 Richard Schulz 的支持在单个算法的实现和 John Paparizos、Paul Boniol、Themis Palpanas 和 Felix Naumann 对我们的研究项目的宝贵输入。
这项工作由德国政府资助，作为 LuFo VI 调用 I 程序 (Luftfahrtforschungsprogramm) 的一部分，资助号为 20D1915。 Rolls-Royce Deutschland Ltd. 的管理。& Co.KG 非常感谢支持这项工作并允许呈现结果。

参考文献