Almost Union-Find
支持三种操作

1. 合并$x$和$y$所在的集合
2. 把$x$移到$y$所在的集合
3. 求$x$所在的集合的元素个数和元素之和

操作1和3是基本的并查集的操作.

关键在于操作$2$:
若使用朴素的并查集，把节点$1$合并到$3$所在的集合，会同时也把1的儿子节点$2$也移动过去，这不是我们想要的。（这里借用luogu题解区的图片）

我们可以通过给每个元素设置一个虚拟父节点，每次移动的时候操作的是实际的节点，而不是父节点即可完成。因为这个时候操作的节点都是叶子节点，不会有副作用。

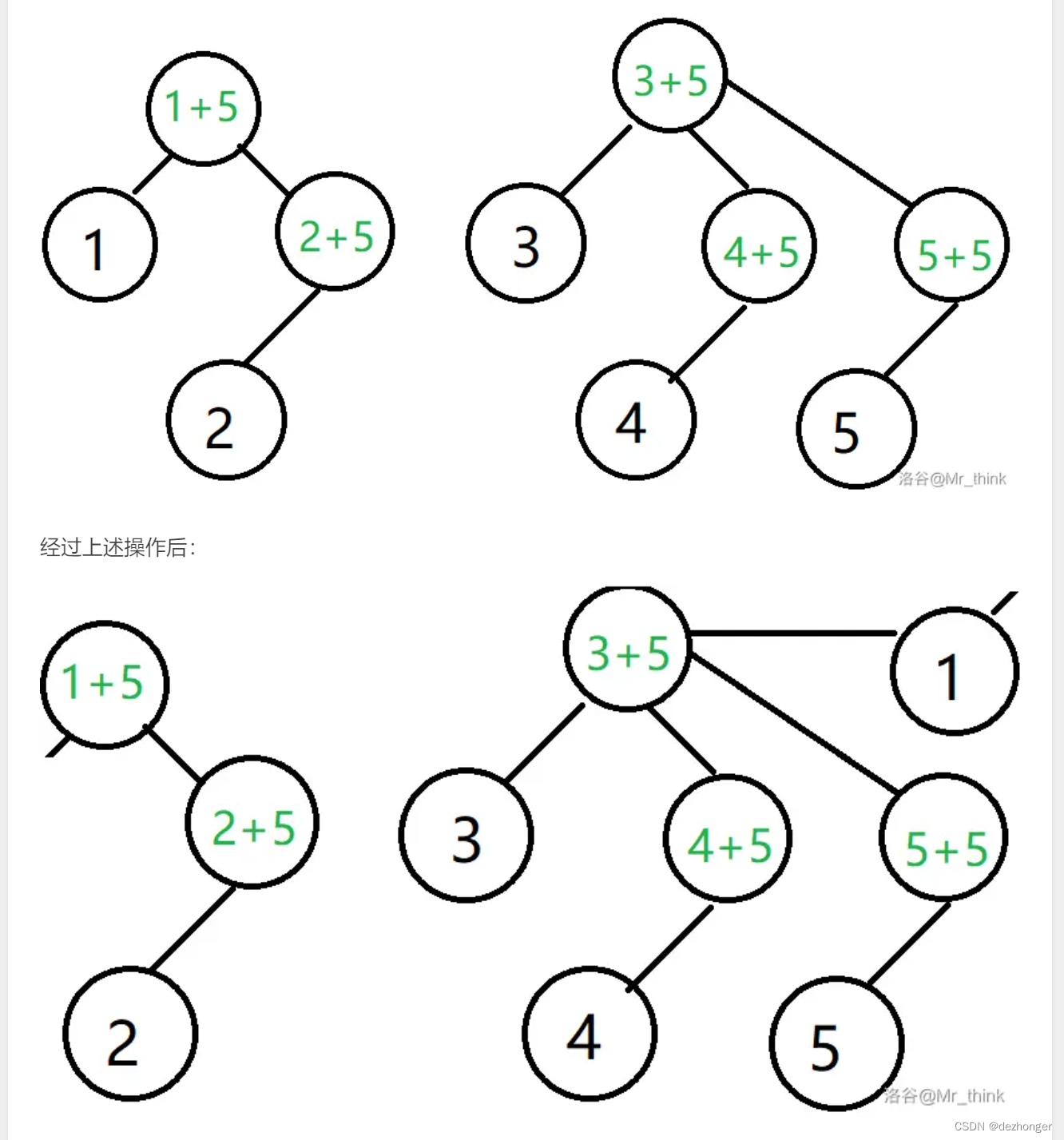
代码中的下标从$0$开始，因此在输入输出的时候有特殊处理。操作2对应于$DSU$的$move$函数.

#include <bits/stdc++.h>
using namespace std;#ifdef LOCAL
#include "debug.h"
#else
#define debug(...) 42
#endiftypedef long long LL;struct DSU {std::vector<int> f, siz;// 集合内的元素和std::vector<long long> s;DSU() {}DSU(int n) {init(n);}void init(int n) {f.resize(n * 2);siz.resize(n * 2);s.resize(n * 2);// 每个点有一个虚点，对应的编号为: i+n, 虚点的父亲指向自己for (int i = n; i < n + n; i++) {f[i - n] = i;f[i] = i;siz[i] = 1;s[i] = i - n;}}int find(int x) {while (x != f[x]) {x = f[x] = f[f[x]];}return x;}bool same(int x, int y) {return find(x) == find(y);}bool merge(int x, int y) {x = find(x);y = find(y);if (x == y) {return false;}siz[x] += siz[y];s[x] += s[y];f[y] = x;return true;}// 把y添加到x的集合bool move(int x, int y) {int u = find(x), v = find(y);if (u == v) {return false;}// 注意这里的变量，y是叶子节点f[y] = u;siz[u]++, siz[v]--;s[u] += y, s[v] -= y;return true;}int size(int x) {return siz[find(x)];}int sum(int x) {return s[find(x)];}
};int main() {int n, m;while (cin >> n >> m){DSU dsu(n);while (m--) {int op, p, q;cin >> op;if (op == 1) {cin >> p >> q;dsu.merge(p - 1, q - 1);} else if (op == 2) {cin >> p >> q;dsu.move(q - 1, p - 1);} else {cin >> p;cout << dsu.size(p - 1) << " " << dsu.sum(p - 1) + dsu.size(p - 1) << endl;}}}return 0;
}