【数据结构】哈夫曼树（Huffman Tree）和哈夫曼编码（Huffman Coding）

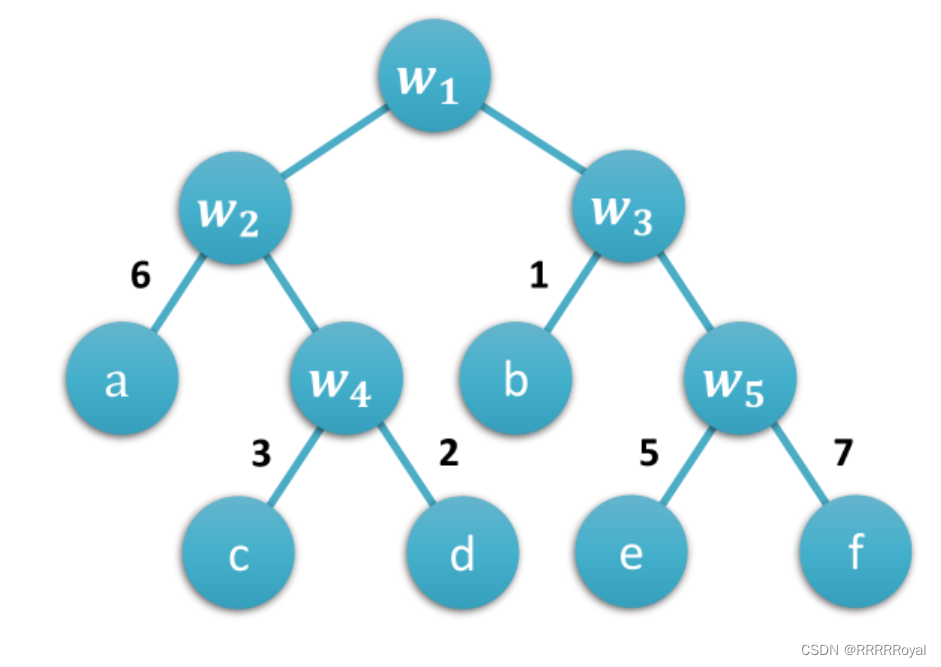
在这里插入图片描述

哈夫曼树（Huffman Tree）和哈夫曼编码（Huffman Coding）是数据压缩领域常用的技术。哈夫曼树是一种特殊的二叉树，用于构造哈夫曼编码，而哈夫曼编码则是一种变长编码，用于压缩数据。

在解释哈夫曼树和哈夫曼编码之前，我们先来了解一下如何构建哈夫曼树。

频率统计：首先，需要对待压缩的数据进行频率统计，统计每个字符出现的频率。频率越高的字符，其在哈夫曼编码中的表示越短。
构建节点：根据统计结果，将每个字符及其对应的频率作为节点。每个节点初始时作为一个独立的子树。
构建哈夫曼树：重复以下步骤，直到只剩下一个节点：
a. 选择两个频率最低的节点，合并它们，生成一个新的节点，该节点的频率为两个节点的频率之和。
b. 将新生成的节点作为子树，再次进行排序。
哈夫曼树生成：最终，生成的树的根节点即为哈夫曼树的根节点。

一旦构建了哈夫曼树，就可以根据树的结构来生成对应的哈夫曼编码。

从根节点开始，沿着左子树路径到达叶子节点时，添加一个"0"到编码中；沿着右子树路径到达叶子节点时，添加一个"1"到编码中。
遍历整棵哈夫曼树，生成每个字符的哈夫曼编码。注意，由于每个字符都能找到唯一的路径，哈夫曼编码是没有前缀的，也就是说，一个字符的哈夫曼编码不是另一个字符的前缀。

通过上述方法，我们就成功地构建了哈夫曼树和哈夫曼编码。接下来，我们可以利用生成的哈夫曼编码来压缩数据。

压缩数据的过程就是将原始数据中的每个字符替换为对应的哈夫曼编码，并将所有替换后的二进制串按位存储。这样，在传输或存储数据时，可以大大减少原始数据的大小。

解压数据的过程相对简单，只需要根据哈夫曼编码和哈夫曼树的对应关系，将编码逐位地进行解码，还原出原始的字符序列。

总结一下，哈夫曼树和哈夫曼编码通过统计字符频率来构建一种具有最优编码的树结构，用于数据压缩和解压缩。通过构建哈夫曼树和生成哈夫曼编码，我们可以将数据压缩到更小的空间，提高数据传输和存储的效率。
以下是一个使用C++面向过程编写的示例代码，展示了如何构建哈夫曼树和生成哈夫曼编码。

#include <iostream>
#include <queue>
#include <map>
using namespace std;// 定义节点结构体
struct Node {char data;int frequency;Node* left;Node* right;
};// 创建节点
Node* createNode(char data, int frequency, Node* left, Node* right) {Node* newNode = new Node();newNode->data = data;newNode->frequency = frequency;newNode->left = left;newNode->right = right;return newNode;
}// 释放节点及其子树的内存
void releaseNode(Node* node) {if (node) {releaseNode(node->left);releaseNode(node->right);delete node;}
}// 定义比较函数用于优先队列排序
struct Compare {bool operator()(const Node* a, const Node* b) {return a->frequency > b->frequency;}
};// 构建哈夫曼树
Node* buildHuffmanTree(map<char, int> frequencies) {priority_queue<Node*, vector<Node*>, Compare> pq;// 将每个字符的频率作为独立节点加入优先队列for (auto pair : frequencies) {Node* newNode = createNode(pair.first, pair.second, nullptr, nullptr);pq.push(newNode);}// 构建哈夫曼树while (pq.size() > 1) {Node* left = pq.top();pq.pop();Node* right = pq.top();pq.pop();int totalFrequency = left->frequency + right->frequency;Node* newNode = createNode('\0', totalFrequency, left, right);pq.push(newNode);}return pq.top();
}// 生成哈夫曼编码
void generateHuffmanCode(Node* root, string code, map<char, string>& huffmanCodes) {if (root == nullptr) {return;}if (root->left == nullptr && root->right == nullptr) {huffmanCodes[root->data] = code;}generateHuffmanCode(root->left, code + "0", huffmanCodes);generateHuffmanCode(root->right, code + "1", huffmanCodes);
}int main() {string input = "hello world";map<char, int> frequencies;// 统计每个字符的频率for (char c : input) {frequencies[c]++;}// 构建哈夫曼树Node* root = buildHuffmanTree(frequencies);// 生成哈夫曼编码map<char, string> huffmanCodes;generateHuffmanCode(root, "", huffmanCodes);// 输出每个字符及其对应的哈夫曼编码for (auto pair : huffmanCodes) {cout << pair.first << " : " << pair.second << endl;}// 释放节点内存releaseNode(root);return 0;
}