语音信号处理：librosa

1 librosa介绍

Librosa是一个用于音频和音乐分析的Python库，专为音乐信息检索（Music Information Retrieval，MIR）社区设计。自从2015年首次发布以来，Librosa已成为音频分析和处理领域中最受欢迎的工具之一。它提供了一套清晰、高效的函数来处理音频信号，并提取音乐和音频中的信息。

Librosa在音乐和音频分析方面提供了强大而灵活的工具，适用于从基础研究到实际应用的各个层面。它的广泛应用和强大功能使其成为音频分析领域的重要工具之一。与其他工具相比，Librosa存在如下优势：

易用性： Librosa的API设计简洁直观，便于快速上手和使用。
功能丰富：提供了广泛的音频分析和处理功能。
灵活性：可以轻松集成到更复杂的音频处理和机器学习流程中。
社区支持：强大的社区支持确保了持续的发展和维护。

官网地址：https://librosa.org/doc/latest/index.html

1.1 核心特性

1.1.1 音频信号处理

读取和写入： Librosa支持读取和写入多种格式的音频文件，包括常见的WAV、MP3、FLAC等。
重采样：支持对音频信号进行重采样，即改变音频的采样率。

1.1.2 音频特征提取

频谱特征：包括短时傅里叶变换（STFT）、梅尔频谱（Mel-spectrogram）、色度频谱（Chromagram）等。
时域特征：如零交叉率（Zero-Crossing Rate）、能量（RMS Energy）等。

1.1.3 音乐节拍和节奏分析

节拍跟踪：自动检测音频中的节拍和节奏。
时序分段：根据节奏将音乐分割成小段。

1.1.4 音高和音调检测

音高提取：从音频信号中提取音高信息，用于旋律分析和音乐转录。
音调识别：识别音频片段中的音调。

1.2 应用领域

1.2.1 音乐信息检索

音乐分类和标注：根据音频特征将音乐自动分类，如流派、情感等。
音乐推荐系统：根据音频分析提供个性化音乐推荐。

1.2.2 音频分析

语音处理：在语音识别和语音合成中分析语音信号。
环境声音识别：识别和分类环境中的各种声音。

1.2.3 音乐制作和编辑

自动音乐剪辑：根据节奏和节拍自动剪辑音乐。
音乐可视化：制作音乐的频谱可视化。

1.3 常用函数

load: 加载音频文件
stft: 短时傅里叶变换
istft: 短时傅里叶逆变换
magphase: 将STFT表示转换为幅度和相位表示
mel: 计算梅尔频率
melspectrogram: 计算梅尔频谱
mfcc: 计算MFCC系数
chroma_stft: 计算STFT表示的色度分布
onset_detect: 检测音频信号的起点
tempogram: 计算节奏图
beat_track: 通过节奏图确定节拍位置
cqt: 计算常量Q变换
cqt_hz_to_note: 将频率转换为音符
note_to_hz: 将音符转换为频率

2 librosa使用

2.1 librosa安装

pip install librosa

2.2 加载音频文件

函数原型：

librosa.load(path, sr=22050, mono=True, offset=0.0, duration=None)

读取音频文件，默认采样率是22050，如果要保留音频的原始采样率，使用sr = None。

参数：

path ：音频文件的路径。

sr ：采样率，如果为“None”使用音频自身的采样率

mono ：bool，是否将信号转换为单声道

offset ：float，在此时间之后开始阅读（以秒为单位）

持续时间：float，仅加载这么多的音频（以秒为单位）

返回：

y ：音频时间序列

sr ：音频的采样率

librosa.load 函数返回的时间序列是一个一维数组，表示音频信号在时间轴上的采样值。在 librosa中，时间轴的方向是沿着数组的第一个轴，即 axis=0。
因此，数组的每个元素代表了时间轴上的一个采样点。例如，如果采样率为22050Hz，那么每秒会有 22050 个采样点，我们可以将其理解为在时间轴上每隔1/22050秒就采集一次音频信号的值。
因此，如果音频的长度为T秒，那么librosa.load函数返回的时间序列就是一个长度为T×sr的一维数组，其中sr是采样率。
需要注意的是，返回的时间序列并不一定是归一化的，也不一定是整数类型。在后续的处理中，我们通常需要对其进行归一化、类型转换等操作。

import librosaaudio_data = '../data/mel001.wav'
data, sr = librosa.load(audio_data)
print('采样率：', sr)
print('数据长度：', data.shape)
print('数据：', data)

运行代码显示：

采样率： 22050
数据长度： (4879296,)
数据： [0. 0. 0. ... 0. 0. 0.]

2.3 重采样

函数原型：

librosa.resample(y, orig_sr, target_sr, fix=True, scale=False)

重新采样从orig_sr到target_sr的时间序列

参数：

y ：音频时间序列。可以是单声道或立体声。

orig_sr ：y的原始采样率

target_sr ：目标采样率

fix：bool，调整重采样信号的长度，使其大小恰好为len(y)/orig_sr*target_sr=t∗target_sr

scale：bool，缩放重新采样的信号，以使y和y_hat具有大约相等的总能量。

返回：

y_hat ：重采样之后的音频数组

示例代码：

import librosaaudio_data = '../data/mel001.wav'
data, sr = librosa.load(audio_data)y_hat = librosa.resample(data, orig_sr=22050, target_sr=44100)
print('原始数据长度：', data.shape)
print('重采样后数据长度：', y_hat.shape)

运行代码显示：

原始数据长度： (4879296,)
重采样后数据长度： (9758592,)

2.4 读取时长

函数原型：

librosa.get_duration(y=None, sr=22050, S=None, n_fft=2048, hop_length=512, center=True, filename=None)

计算时间序列的的持续时间（以秒为单位）

参数：

y ：音频时间序列

sr ：y的音频采样率

S ：STFT矩阵或任何STFT衍生的矩阵（例如，色谱图或梅尔频谱图）。根据频谱图输入计算的持续时间仅在达到帧分辨率之前才是准确的。如果需要高精度，则最好直接使用音频时间序列。

n_fft ：S的 FFT窗口大小

hop_length ：S列之间的音频样本数

center ：布尔值

如果为True，则S [:, t]的中心为y [t * hop_length]

如果为False，则S [:, t]从y[t * hop_length]开始

filename ：如果提供，则所有其他参数都将被忽略，并且持续时间是直接从音频文件中计算得出的。

返回：

d ：持续时间（以秒为单位）

示例代码：

import librosaaudio_data = '../data/mel001.wav'
data, sr = librosa.load(audio_data)
y_hat = librosa.resample(data, orig_sr=22050, target_sr=44100)
duration1 = librosa.get_duration(y=data)
duration2 = librosa.get_duration(y=y_hat, sr=44100)
print('原始时长：', duration1)
print('重采样后时长：', duration2)

运行代码显示：

原始时长： 221.28326530612244
重采样后时长： 221.28326530612244

2.5 读取采样率

函数原型：

librosa.get_samplerate(path)

参数：

path ：音频文件的路径

返回：音频文件的采样率

示例代码：

import librosaaudio_data = '../data/mel001.wav'
sr = librosa.get_samplerate(audio_data)
print('采样率：', sr)

运行代码显示：

采样率： 44100

2.6 写音频

函数原型：

librosa.output.write_wav(path, y, sr, norm=False)

将时间序列输出为.wav文件

参数：

path：保存输出wav文件的路径

y ：音频时间序列。

sr ：y的采样率

norm：bool，是否启用幅度归一化。将数据缩放到[-1，+1]范围。

在0.8.0以后的版本，librosa这个函数已经删除，推荐用下面的函数：

import soundfile
soundfile.write(file, data, samplerate)

参数：

file：保存输出wav文件的路径

data：音频数据

samplerate：采样率

示例代码：

import librosa
import soundfileaudio_data = '../data/mel001.wav'
data, sr = librosa.load(audio_data)
y_hat = librosa.resample(data, orig_sr=22050, target_sr=44100)
soundfile.write('../data/re_mel001.wav', data, 44100)

2.7 过零率

函数原型：

librosa.feature.zero_crossing_rate(y, frame_length = 2048, hop_length = 512, center = True)

计算音频时间序列的过零率。

参数：

y ：音频时间序列

frame_length ：帧长

hop_length ：帧移

center：bool，如果为True，则通过填充y的边缘来使帧居中。

返回：

zcr：zcr[0，i]是第i帧中的过零率

示例代码：

import librosaaudio_data = '../data/mel001.wav'
data, sr = librosa.load(audio_data, sr=44100)
print(librosa.feature.zero_crossing_rate(data))
print(data.shape)

运行代码显示：

[[0. 0. 0. ... 0. 0. 0.]]
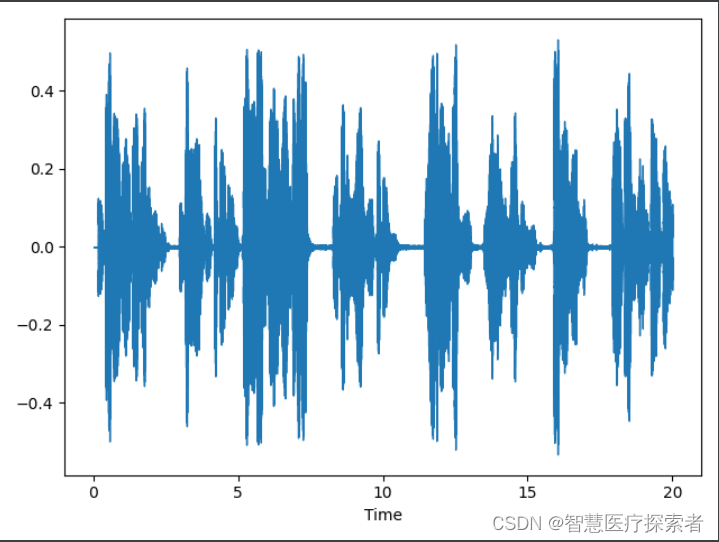
(9758592,)

2.8 波形图

函数原型：

librosa.display.waveshow(y,*,sr=22050,max_points=11025,x_axis="time",offset=0.0,marker="",where="post",label=None,ax=None,**kwargs,)

绘制波形的幅度包络线

参数：

y ：音频时间序列

sr ：y的采样率

x_axis ：str {‘time’，‘off’，‘none’}或None，如果为“时间”，则在x轴上给定时间刻度线。

offset：水平偏移（以秒为单位）开始波形图

示例代码：

import librosa
import librosa.display
import matplotlib.pyplot as plty, sr = librosa.load('../data/mel001.wav', duration=20)
librosa.display.waveshow(y, sr=sr)
plt.show()

运行代码显示：

2.9 短时傅里叶变换

librosa.stft(y, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')

短时傅立叶变换（STFT），返回一个复数矩阵D(F，T)

参数：

y：音频时间序列

n_fft：FFT窗口大小，n_fft=hop_length+overlapping

hop_length：帧移，如果未指定，则默认win_length/4。

win_length：每一帧音频都由window（）加窗。窗长win_length，然后用零填充以匹配N_FFT。默认win_length=n_fft。

window：字符串，元组，数字，函数 shape =（n_fft, )

            窗口（字符串，元组或数字）；

            窗函数，例如scipy.signal.hanning

            长度为n_fft的向量或数组

center：bool

            如果为True，则填充信号y，以使帧 D [:, t]以y [t * hop_length]为中心。

            如果为False，则D [:, t]从y [t * hop_length]开始

dtype：D的复数值类型。默认值为64-bit complex复数

pad_mode：如果center = True，则在信号的边缘使用填充模式。默认情况下，STFT使用reflection padding。

返回：

STFT矩阵，shape =（1 + n(fft)/2，t）

2.10 幅值和相位

函数原型：

librosa.magphase(D, power=1)

librosa提供了专门将复数矩阵D(F, T)分离为幅值S和相位P的函数，D = S * P

参数：

D：经过stft得到的复数矩阵
power：幅度谱的指数，例如，1代表能量，2代表功率，等等。

返回：

D_mag：幅值D，
D_phase：相位P， phase = exp(1.j * phi) ， phi 是复数矩阵的相位角 np.angle(D)

2.11 短时傅里叶逆变换

函数原型：

librosa.istft(stft_matrix, hop_length=None, win_length=None, window='hann', center=True, length=None)

短时傅立叶逆变换（ISTFT），将复数值D(f,t)频谱矩阵转换为时间序列y，窗函数、帧移等参数应与stft相同

参数：

stft_matrix ：经过STFT之后的矩阵

hop_length ：帧移，默认为 $eq?%5Cfrac%7B%5E%7Bwin_%7Blenth%7D%7D%7D%7B4%7D$

win_length ：窗长，默认为n_fft

window：字符串，元组，数字，函数或shape = (n_fft, )

        窗口（字符串，元组或数字）
        窗函数，例如scipy.signal.hanning
        长度为n_fft的向量或数组

center：bool

        如果为True，则假定D具有居中的帧
        如果False，则假定D具有左对齐的帧

length：如果提供，则输出y为零填充或剪裁为精确长度音频

返回：

y ：时域信号

2.12 功率转dB

函数原型

librosa.core.power_to_db(S, ref=1.0)

将功率谱(幅值平方)转换为dB单位，与这个函数相反的是 librosa.db_to_power(S)

参数：

S：输入功率

ref ：参考值，振幅abs(S)相对于ref进行缩放

返回：

dB为单位的S， $ref%7D$

示例代码：

import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plty, sr = librosa.load('../data/mel001.wav')
S = np.abs(librosa.stft(y))     # 幅值
print(librosa.power_to_db(S ** 2))
plt.figure()
plt.subplot(2, 1, 1)
librosa.display.specshow(S ** 2, sr=sr, y_axis='log')  # 绘制功率谱
plt.colorbar()
plt.title('Power spectrogram')
plt.subplot(2, 1, 2)
# 相对于峰值功率计算dB, 那么其他的dB都是负的，注意看后边cmp值
librosa.display.specshow(librosa.power_to_db(S ** 2, ref=np.max), sr=sr, y_axis='log', x_axis='time')   # 绘制对数功率谱
plt.colorbar(format='%+2.0f dB')
plt.title('Log-Power spectrogram')
plt.set_cmap("autumn")
plt.tight_layout()
plt.show()

运行代码显示：

[[-35.042385 -35.042385 -35.042385 ... -35.042385 -35.042385 -35.042385][-35.042385 -35.042385 -35.042385 ... -35.042385 -35.042385 -35.042385][-35.042385 -35.042385 -35.042385 ... -35.042385 -35.042385 -35.042385]...[-35.042385 -35.042385 -35.042385 ... -35.042385 -35.042385 -35.042385][-35.042385 -35.042385 -35.042385 ... -35.042385 -35.042385 -35.042385][-35.042385 -35.042385 -35.042385 ... -35.042385 -35.042385 -35.042385]]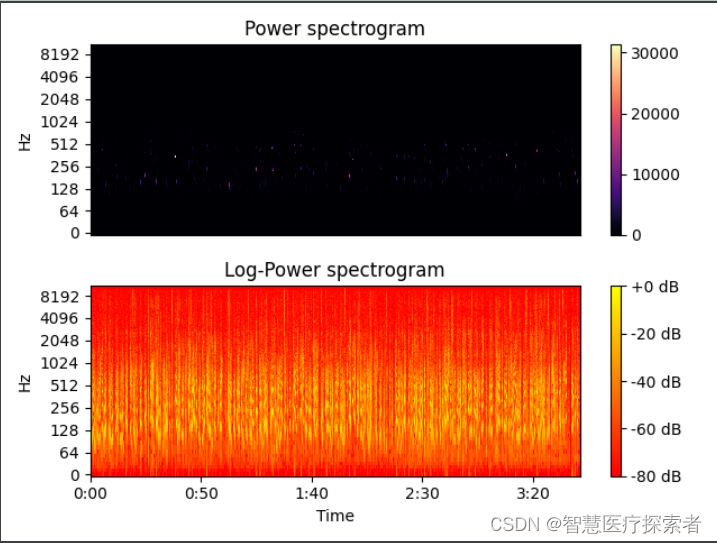

2.13 绘制频谱图

librosa.display.specshow(data, x_axis=None, y_axis=None, sr=22050, hop_length=512)

参数：

data：要显示的矩阵

sr ：采样率

hop_length ：帧移

x_axis 、y_axis ：x和y轴的范围

频率类型

‘linear’，‘fft’，‘hz’：频率范围由FFT窗口和采样率确定

‘log’：频谱以对数刻度显示

‘mel’：频率由mel标度决定

时间类型

time：标记以毫秒，秒，分钟或小时显示。值以秒为单位绘制。

s：标记显示为秒。

ms：标记以毫秒为单位显示。

所有频率类型均以Hz为单位绘制

import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plty, sr = librosa.load('../data/mel001.wav')
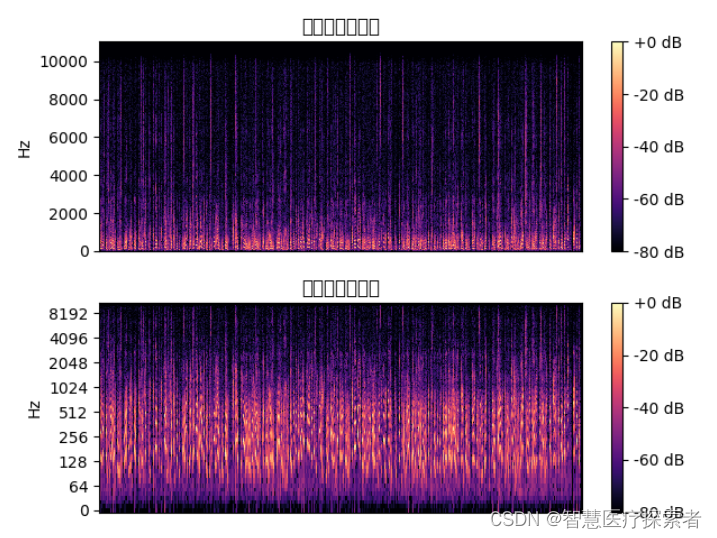
plt.figure()D = librosa.amplitude_to_db(np.abs(librosa.stft(y)), ref=np.max)
plt.subplot(2, 1, 1)
librosa.display.specshow(D, y_axis='linear')
plt.colorbar(format='%+2.0f dB')
plt.title('线性频率功率谱')plt.subplot(2, 1, 2)
librosa.display.specshow(D, y_axis='log')
plt.colorbar(format='%+2.0f dB')
plt.title('对数频率功率谱')
plt.show()

运行代码显示：

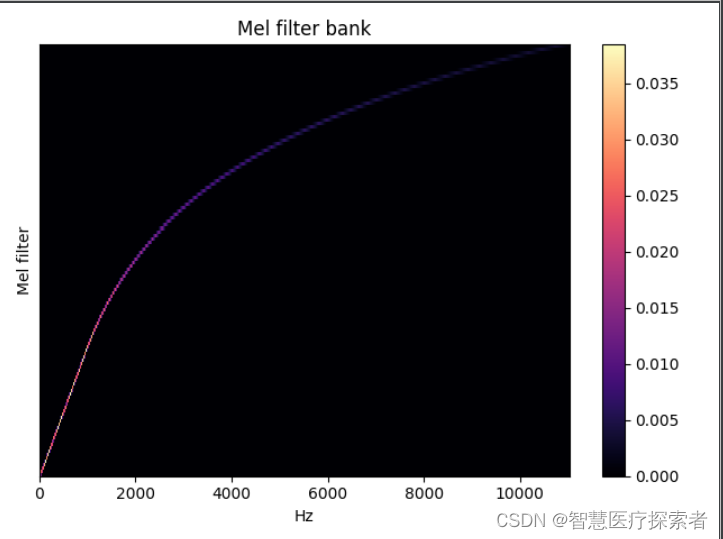
2.14 Mel滤波器组

librosa.filters.mel(sr, n_fft, n_mels=128, fmin=0.0, fmax=None, htk=False, norm=1)

创建一个滤波器组矩阵以将FFT合并成Mel频率

参数：

sr ：输入信号的采样率

n_fft ：FFT组件数

n_mels ：产生的梅尔带数

fmin ：最低频率（Hz）

fmax：最高频率（以Hz为单位）。如果为None，则使用fmax = sr / 2.0

norm：{None，1，np.inf} [标量]

如果为1，则将三角mel权重除以mel带的宽度（区域归一化）。否则，保留所有三角形的峰值为1.0

返回：

Mel变换矩阵

import librosa
import librosa.display
import matplotlib.pyplot as pltmelfb = librosa.filters.mel(sr=22050, n_fft=2048)
plt.figure()
librosa.display.specshow(melfb, x_axis='linear')
plt.ylabel('Mel filter')
plt.title('Mel filter bank')
plt.colorbar()
plt.tight_layout()
plt.show()

运行代码显示：

2.15 计算Mel频谱

librosa.feature.melspectrogram(y=None, sr=22050, S=None, n_fft=2048, hop_length=512, win_length=None, window='hann', center=True, pad_mode='reflect', power=2.0)

如果提供了频谱图输入S，则通过mel_f.dot（S）将其直接映射到mel_f上。如果提供了时间序列输入y，sr，则首先计算其幅值频谱S，然后通过mel_f.dot（S ** power）将其映射到mel scale上。默认情况下，power= 2在功率谱上运行。

参数：

y ：音频时间序列

sr ：采样率

S ：频谱

n_fft ：FFT窗口的长度

hop_length ：帧移

win_length ：窗口的长度为win_length，默认win_length = n_fft

window ：字符串，元组，数字，函数或shape =（n_fft, )

        窗口规范（字符串，元组或数字）；看到scipy.signal.get_window
        窗口函数，例如 scipy.signal.hanning
        长度为n_fft的向量或数组

center：bool

        如果为True，则填充信号y，以使帧 t以y [t * hop_length]为中心。
        如果为False，则帧t从y [t * hop_length]开始

power：幅度谱的指数。例如1代表能量，2代表功率，等等

n_mels：滤波器组的个数 1288

fmax：最高频率

返回：

Mel频谱shape=(n_mels, t)

import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plty, sr = librosa.load('../data/mel001.wav')
# 方法一：使用时间序列求Mel频谱
print(librosa.feature.melspectrogram(y=y, sr=sr))# 方法二：使用stft频谱求Mel频谱
D = np.abs(librosa.stft(y)) ** 2  # stft频谱
S = librosa.feature.melspectrogram(S=D)  # 使用stft频谱求Mel频谱plt.figure(figsize=(10, 4))
librosa.display.specshow(librosa.power_to_db(S, ref=np.max), y_axis='mel', fmax=8000, x_axis='time')
plt.colorbar(format='%+2.0f dB')
plt.title('Mel spectrogram')
plt.tight_layout()
plt.show()

运行代码显示：

[[0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.]...[0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.]]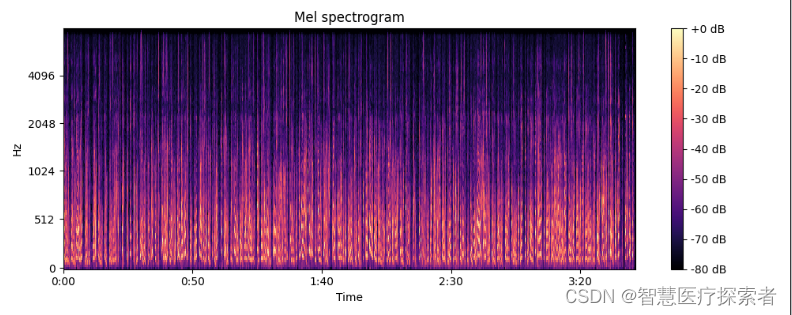

2.16 提取Log-Mel Spectrogram特征

Log-Mel Spectrogram特征是目前在语音识别和环境声音识别中很常用的一个特征，由于CNN在处理图像上展现了强大的能力，使得音频信号的频谱图特征的使用愈加广泛，甚至比MFCC使用的更多。在librosa中，Log-Mel Spectrogram特征的提取只需几行代码：

import librosay, sr = librosa.load('../data/mel001.wav', sr=16000)# 提取 mel spectrogram feature
melspec = librosa.feature.melspectrogram(y=y, sr=sr, n_fft=1024, hop_length=512, n_mels=128)# 转换到对数刻度
logmelspec = librosa.power_to_db(melspec)
print(logmelspec.shape)

运行代码显示：

(128, 6916)

可见，Log-Mel Spectrogram特征是二维数组的形式，128表示Mel频率的维度（频域），64为时间帧长度（时域），所以Log-Mel Spectrogram特征是音频信号的时频表示特征。其中，n_fft指的是窗的大小，这里为1024；hop_length表示相邻窗之间的距离，这里为512，也就是相邻窗之间有50%的overlap；n_mels为mel bands的数量，这里设为128。

2.17 提取MFCC系数

MFCC特征是一种在自动语音识别和说话人识别中广泛使用的特征。在librosa中，提取MFCC特征只需要一个函数：

librosa.feature.mfcc(y=None, sr=22050, S=None, n_mfcc=20, dct_type=2, norm='ortho', **kwargs)

参数：

y：音频数据

sr：采样率

S：np.ndarray，对数功能梅尔谱图

n_mfcc：int>0，要返回的MFCC数量

dct_type：None, or {1, 2, 3} 离散余弦变换（DCT）类型。默认情况下，使用DCT类型2。

norm： None or ‘ortho’ 规范。如果dct_type为2或3，则设置norm =’ortho’使用正交DCT基础。标准化不支持dct_type = 1。

返回：

M： MFCC序列

import librosay, sr = librosa.load('../data/mel001.wav', sr=16000)# 提取 MFCC feature
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=40)
print(mfccs.shape)

运行代码显示：

(40, 6916)

线性谱、梅尔谱、对数谱：经过FFT变换后得到语音数据的线性谱，对线性谱取Mel系数，得到梅尔谱；对线性谱取对数，得到对数谱。

3 librosa函数集

2.1 Audio loading

load(path, *[, sr, mono, offset, duration, ...])	Load an audio file as a floating point time series.
stream(path, *, block_length, frame_length, ...)	Stream audio in fixed-length buffers.
to_mono(y)	Convert an audio signal to mono by averaging samples across channels.
resample(y, *, orig_sr, target_sr[, ...])	Resample a time series from orig_sr to target_sr
get_duration(*[, y, sr, S, n_fft, ...])	Compute the duration (in seconds) of an audio time series, feature matrix, or filename.
get_samplerate(path)	Get the sampling rate for a given fil

2.2 Time-domain processing

autocorrelate(y, *[, max_size, axis])	Bounded-lag auto-correlation
lpc(y, *, order[, axis])	Linear Prediction Coefficients via Burg's method
zero_crossings(y, *[, threshold, ...])	Find the zero-crossings of a signal `y`: indices `i` such that `sign(y[i]) != sign(y[j])`.
mu_compress(x, *[, mu, quantize])	mu-law compression
mu_expand(x, *[, mu, quantize])	mu-law expansion

2.3 Signal generation

clicks(*[, times, frames,

sr, hop_length, ...])

Construct a "click track".

tone(frequency, *[, sr, length,

duration, phi])

Construct a pure tone (cosine) signal at a given frequency.

chirp(*, fmin, fmax[, sr,

length, duration, ...])

Construct a "chirp" or "sine-sweep" signal.

2.4 Spectral representations

stft(y, *[, n_fft, hop_length, win_length, ...])	Short-time Fourier transform (STFT).
istft(stft_matrix, *[, hop_length, ...])	Inverse short-time Fourier transform (ISTFT).
reassigned_spectrogram(y, *[, sr, S, n_fft, ...])	Time-frequency reassigned spectrogram.
cqt(y, *[, sr, hop_length, fmin, n_bins, ...])	Compute the constant-Q transform of an audio signal.
icqt(C, *[, sr, hop_length, fmin, ...])	Compute the inverse constant-Q transform.
hydrid_cqt(y, *[, sr, hop_length, fmin, ...])	Compute the hybrid constant-Q transform of an audio signal.
pseudo_cqt(y, *[, sr, hop_length, fmin, ...])	Compute the pseudo constant-Q transform of an audio signal.
vqt(y, *[, sr, hop_length, fmin, n_bins, ...])	Compute the variable-Q transform of an audio signal.
iirt(y, *[, sr, win_length, hop_length, ...])	Time-frequency representation using IIR filters
fmt(y, *[, t_min, n_fmt, kind, beta, ...])	Fast Mellin transform (FMT)
magphase(D, *[, power])	Separate a complex-valued spectrogram D into its magnitude (S) and phase (P) components, so that `D = S * P`.

2.5 Phase recovery

griffinlim(S, *[, n_iter,

hop_length, ...])

Approximate magnitude spectrogram inversion using the "fast" Griffin-Lim algorithm.

griffinlim_cqt(C, *[, n_iter, sr, ...])

Approximate constant-Q magnitude spectrogram inversion using the "fast" Griffin-Lim algorithm.

2.6 Harmonics

interp_harmonics(x, *, freqs, harmonics[, ...])	Compute the energy at harmonics of time-frequency representation.
salience(S, *, freqs, harmonics[, weights, ...])	Harmonic salience function.
f0_harmonics(x, *, f0, freqs, harmonics[, ...])	Compute the energy at selected harmonics of a time-varying fundamental frequency.
phase_vocoder(D, *, rate[, hop_length, n_fft])	Phase vocoder.

2.7 Magnitude scaling

amplitude_to_db(S, *[, ref, amin, top_db])	Convert an amplitude spectrogram to dB-scaled spectrogram.
db_to_amplitude(S_db, *[, ref])	Convert a dB-scaled spectrogram to an amplitude spectrogram.
power_to_db(S, *[, ref, amin, top_db])	Convert a power spectrogram (amplitude squared) to decibel (dB) units
db_to_power(S_db, *[, ref])	Convert a dB-scale spectrogram to a power spectrogram.
perceptual_weighting(S, frequencies, *[, kind])	Perceptual weighting of a power spectrogram.
frequency_weighting(frequencies, *[, kind])	Compute the weighting of a set of frequencies.
multi_frequency_weighting( frequencies, *[, ...])	Compute multiple weightings of a set of frequencies.
A_weighting(frequencies, *[, min_db])	Compute the A-weighting of a set of frequencies.
B_weighting(frequencies, *[, min_db])	Compute the B-weighting of a set of frequencies.
C_weighting(frequencies, *[, min_db])	Compute the C-weighting of a set of frequencies.
D_weighting(frequencies, *[, min_db])	Compute the D-weighting of a set of frequencies.
pcen(S, *[, sr, hop_length, gain, bias, ...])	Per-channel energy normalization (PCEN)

2.8 Time unit conversion

frames_to_samples(frames, *[, hop_length, n_fft])	Convert frame indices to audio sample indices.
frames_to_time(frames, *[, sr, hop_length, ...])	Convert frame counts to time (seconds).
samples_to_frames(samples, *[, hop_length, ...])	Convert sample indices into STFT frames.
samples_to_time(samples, *[, sr])	Convert sample indices to time (in seconds).
time_to_frames(times, *[, sr, hop_length, n_fft])	Convert time stamps into STFT frames.
time_to_samples(times, *[, sr])	Convert timestamps (in seconds) to sample indices.
blocks_to_frames(blocks, *, block_length)	Convert block indices to frame indices
blocks_to_samples(blocks, *, block_length, ...)	Convert block indices to sample indices
blocks_to_time(blocks, *, block_length, ...)	Convert block indices to time (in seconds)

2.9 Frequency unit conversion

hz_to_note(frequencies, **kwargs)	Convert one or more frequencies (in Hz) to the nearest note names.
hz_to_midi(frequencies)	Get MIDI note number(s) for given frequencies
hz_to_svara_h(frequencies, *, Sa[, abbr, ...])	Convert frequencies (in Hz) to Hindustani svara
hz_to_svara_c(frequencies, *, Sa, mela[, ...])	Convert frequencies (in Hz) to Carnatic svara
hz_to_fjs(frequencies, *[, fmin, unison, ...])	Convert one or more frequencies (in Hz) from a just intonation scale to notes in FJS notation.
midi_to_hz(notes)	Get the frequency (Hz) of MIDI note(s)
midi_to_note(midi, *[, octave, cents, key, ...])	Convert one or more MIDI numbers to note strings.
midi_to_svara_h(midi, *, Sa[, abbr, octave, ...])	Convert MIDI numbers to Hindustani svara
midi_to_svara_c(midi, *, Sa, mela[, abbr, ...])	Convert MIDI numbers to Carnatic svara within a given melakarta raga
note_to_hz(note, **kwargs)	Convert one or more note names to frequency (Hz)
note_to_midi(note, *[, round_midi])	Convert one or more spelled notes to MIDI number(s).
note_to_svara_h(notes, *, Sa[, abbr, ...])	Convert western notes to Hindustani svara
note_to_svara_c(notes, *, Sa, mela[, abbr, ...])	Convert western notes to Carnatic svara
hz_to_mel(frequencies, *[, htk])	Convert Hz to Mels
hz_to_octs(frequencies, *[, tuning, ...])	Convert frequencies (Hz) to (fractional) octave numbers.
mel_to_hz(mels, *[, htk])	Convert mel bin numbers to frequencies
octs_to_hz(octs, *[, tuning, bins_per_octave])	Convert octaves numbers to frequencies.
A4_to_tuning(A4, *[, bins_per_octave])	Convert a reference pitch frequency (e.g., `A4=435`) to a tuning estimation, in fractions of a bin per octave.
tuning_to_A4(tuning, *[, bins_per_octave])	Convert a tuning deviation (from 0) in fractions of a bin per octave (e.g., `tuning=-0.1`) to a reference pitch frequency relative to A440.

2.9 Music notation

key_to_notes(key, *[, unicode])	List all 12 note names in the chromatic scale, as spelled according to a given key (major or minor).
key_to_degress(key)	Construct the diatonic scale degrees for a given key.
mela_to_svara(mela, *[, abbr, unicode])	Spell the Carnatic svara names for a given melakarta raga
mela_to_degress(mela)	Construct the svara indices (degrees) for a given melakarta raga
thaat_to_degress(thaat)	Construct the svara indices (degrees) for a given thaat
list_mela()	List melakarta ragas by name and index.
list_thaat()	List supported thaats by name.
fifths_to_node(*, unison, fifths[, unicode])	Calculate the note name for a given number of perfect fifths from a specified unison.
interval_to_fjs(interval, *[, unison, ...])	Convert an interval to Functional Just System (FJS) notation.
interval_frequencies(n_bins, *, fmin, intervals)	Construct a set of frequencies from an interval set
pythagorean_intervals(*[, bins_per_octave, ...])	Pythagorean intervals
plimit_intervals(*, primes[, ...])	Construct p-limit intervals for a given set of prime factors.

2.9 Frequency range generation

fft_frequencies(*[, sr, n_fft])	Alternative implementation of np.fft.fftfreq
cqt_frequencies(n_bins, *, fmin[, ...])	Compute the center frequencies of Constant-Q bins.
mel_frequencies([n_mels, fmin, fmax, htk])	Compute an array of acoustic frequencies tuned to the mel scale.
tempo_frequencies(n_bins, *[, hop_length, sr])	Compute the frequencies (in beats per minute) corresponding to an onset auto-correlation or tempogram matrix.
fourier_tempo_frequencies(*[, sr, ...])	Compute the frequencies (in beats per minute) corresponding to a Fourier tempogram matrix.

2.10 Pitch and tuning

pyin(y, *, fmin, fmax[, sr, frame_length, ...])	Fundamental frequency (F0) estimation using probabilistic YIN (pYIN).
yin(y, *, fmin, fmax[, sr, frame_length, ...])	Fundamental frequency (F0) estimation using the YIN algorithm.
estimate_tuning(*[, y, sr, S, n_fft, ...])	Estimate the tuning of an audio time series or spectrogram input.
pitch_tuning(frequencies, *[, resolution, ...])	Given a collection of pitches, estimate its tuning offset (in fractions of a bin) relative to A440=440.0Hz.
piptrack(*[, y, sr, S, n_fft, hop_length, ...])	Pitch tracking on thresholded parabolically-interpolated STFT.

2.11 Miscellaneous

samples_like(X, *[, hop_length, n_fft, axis])	Return an array of sample indices to match the time axis from a feature matrix.
times_like(X, *[, sr, hop_length, n_fft, axis])	Return an array of time values to match the time axis from a feature matrix.
get_fftlib()	Get the FFT library currently used by librosa
set_fftlib([lib])	Set the FFT library used by librosa.