给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明 你不能倾斜容器.

示例一

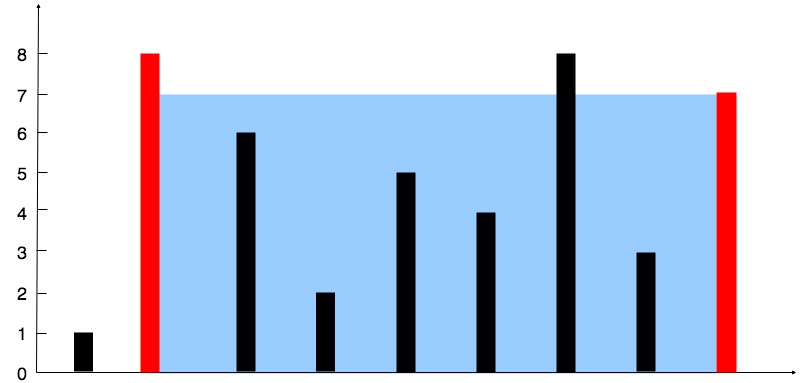
输入：[1,8,6,2,5,4,8,3,7]

输出：49

解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例二

输入：height = [1,1]

输出：1

算法思路: 对撞双指针

设两个指针left, right, 分别指向数组的两个端点, 此时, 容器的体积为v = (right - left) * min(height[left], height[right])

容器的左边界为height[left], 容器的右边界为height[right].

我们假设 右边界小于左边界. v = (right - left) * height[right]

如果我们固定一个边界, 改变另一个边界, 那么容器体积就会有如下变化

• 容器的宽度变小
• 因为右边界比较小, 决定了水的高度. 如果改变右边界, 新的水面高度不确定, 但是一定不会超过左边界, v = h * w, w变小, h都有可能, 所以v的变化不确定
• 如果改变左边界, 无论左边界移动到哪里, 水的高度绝对不可能超过右边界, 那就分为两种情况
  • 水的高度不变, 但是宽度变小, 所以体积变小
  • 谁的高度变小, 宽度变小, 所以体积变小

由此可见, 我们如果移动左边界(边界值大), 那么无论向哪移动, 容器的体积都会减小, 而移动右边界(边界值小)就不一定了, 所以我们应该移动边界值小的一方.

Java代码

class Solution {public int maxArea(int[] height) {int left = 0, right = height.length - 1, ans = 0;while(left < right) {int v = (right - left) * Math.min(height[right], height[left]);ans = Math.max(v, ans);if(height[left] > height[right]) {right--;} else {left++;}}return ans;}
}

时间复杂度: O(N) 空间复杂度: O(1)