例一
给定X的协差阵,对其进行主成分分析,
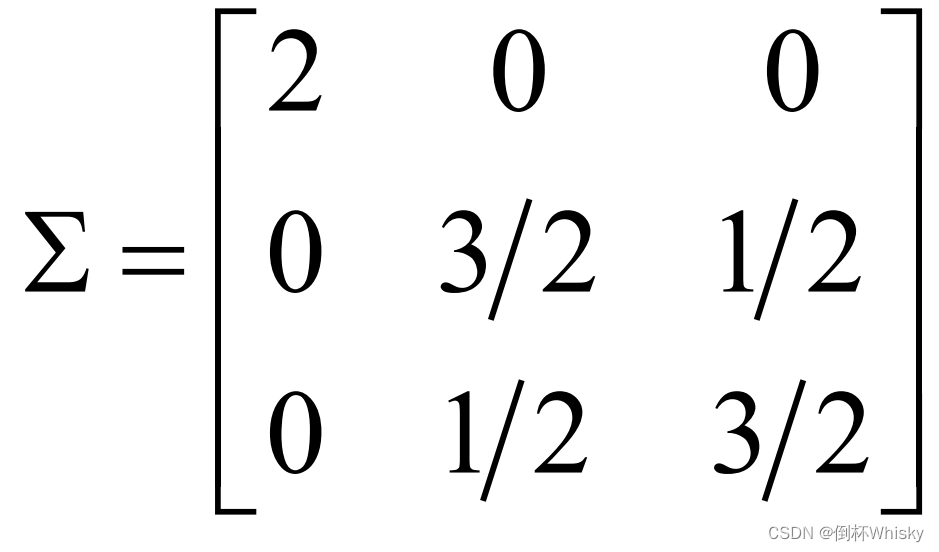
(1)求出每个主成分的贡献率;
(2)求出每个原始变量的信息提取率;
解:对于主成分分析的题,一般来说,题目给定一个协方差阵,不管怎样先求出特征值和特征向量。
Step1 计算特征根
解 ∣ Σ − λ I ∣ |Σ-λI| ∣Σ−λI∣=0,得: λ 1 λ_1 λ1=2, λ 2 λ_2 λ2=2, λ 3 λ_3 λ3=1 ( λ 1 λ_1 λ1≥ λ 2 λ_2 λ2≥ λ 3 λ_3 λ3)
如果解出来不确定或者解不出来的话可以通过特征值的和等于协方差阵对角线元素的和以及特征值的积等于协方差阵对应的行列式来进行验证
Step2 求特征向量,这里一定不能忘记要化成单位特征向量
U 1 = [ 1 0 0 ] U_1=\left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right] U1= 100 U 2 = [ 0 1 2 1 2 ] U_2=\left[ \begin{matrix} 0 \\ {1 \over {\sqrt{2}} } \\ {1 \over {\sqrt{2}} } \end{matrix} \right] U2= 02121 U 3 = [ 0 − 1 2 1 2 ] U_3=\left[ \begin{matrix} 0 \\ -{1 \over {\sqrt{2}} } \\ {1 \over {\sqrt{2}} } \end{matrix} \right] U3= 0−2121
Step3 计算贡献率
第一个主成分的贡献率为: λ 1 λ_1 λ1/( λ 1 λ_1 λ1+ λ 2 λ_2 λ2+ λ 3 λ_3 λ3)=2/5=40%
第二个主成分的贡献率为: λ 2 λ_2 λ2/( λ 1 λ_1 λ1+ λ 2 λ_2 λ2+ λ 3 λ_3 λ3)=2/5=40%
第三个主成分的贡献率为: λ 3 λ_3 λ3/( λ 1 λ_1 λ1+ λ 2 λ_2 λ2+ λ 3 λ_3 λ3)=1/5=20%
(注意这里算的不是累积贡献率)所以我们取前两个主成分就可以了
Step4 求信息提取率
分别计算 x i x_i xi与 F 1 F_1 F1、 F 2 F_2 F2的相关系数的平方,信息提取率为两者之和,
计算相关系数的公式如下
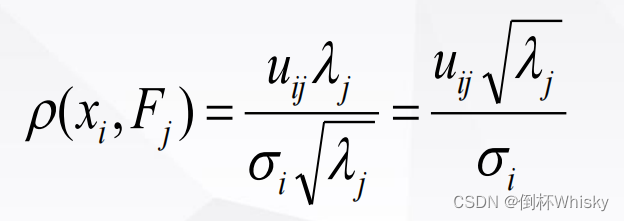
所以x1的信息提取率就是x1与 F 1 F_1 F1相关系数的平方加上x1与 F 2 F_2 F2相关系数的平方,其他原始变量同理。
| x i x_i xi | x i x_i xi与 F 1 F_1 F1相关系数的平方 | x i x_i xi与 F 2 F_2 F2相关系数的平方 | 信息提取率 |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 2/3 | 0.67 |
| 3 | 0 | 2/3 | 0.67 |
例二
设 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3的协方差矩阵如下,试求主成分分析,并求出每个主成分的贡献率及每个原始变量的信息提取率。
Σ = [ 1 − 2 0 − 2 5 0 0 0 2 ] Σ=\left[ \begin{matrix} 1 & -2 & 0 \\ -2 & 5 & 0 \\ 0 & 0 & 2 \end{matrix} \right] Σ= 1−20−250002
解:
Step1 计算特征根
解 ∣ Σ − λ I ∣ |Σ-λI| ∣Σ−λI∣=0,得: λ 1 λ_1 λ1=5.83, λ 2 λ_2 λ2=2, λ 3 λ_3 λ3=0.17 ( λ 1 λ_1 λ1≥ λ 2 λ_2 λ2≥ λ 3 λ_3 λ3)
Step2 求特征向量
U 1 = [ 0.383 − 0.924 0.000 ] U_1=\left[ \begin{matrix} 0.383 \\ -0.924 \\ 0.000 \end{matrix} \right] U1= 0.383−0.9240.000 U 2 = [ 0 0 1 ] U_2=\left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] U2= 001 U 3 = [ 0.924 0.383 0.000 ] U_3=\left[ \begin{matrix} 0.924 \\ 0.383 \\ 0.000 \end{matrix} \right] U3= 0.9240.3830.000
Step3 计算贡献率
第一个主成分的贡献率为: λ 1 λ_1 λ1/( λ 1 λ_1 λ1+ λ 2 λ_2 λ2+ λ 3 λ_3 λ3)=5.83/8=72.875%
第二个主成分的贡献率为: λ 2 λ_2 λ2/( λ 1 λ_1 λ1+ λ 2 λ_2 λ2+ λ 3 λ_3 λ3)=2/8=25%
第三个主成分的贡献率为: λ 3 λ_3 λ3/( λ 1 λ_1 λ1+ λ 2 λ_2 λ2+ λ 3 λ_3 λ3)=0.17/8=2.125%
Step4 求信息提取率
虽然第一个主成分的贡献率不小,但在本题中第一主成分不含第三个原始变量的信息,因此应该取两个主成分
所以分别计算 x i x_i xi与 F 1 F_1 F1 F 2 F_2 F2的相关系数的平方,信息提取率为两者之和
| x i x_i xi | x i x_i xi与 F 1 F_1 F1相关系数的平方 | x i x_i xi与 F 2 F_2 F2相关系数的平方 | 信息提取率 |
|---|---|---|---|
| 1 | 0.855 | 0 | 0.855 |
| 2 | 0.996 | 0 | 0.996 |
| 3 | 0 | 1 | 1 |
到clock_settime())
![[vue3] 使用 vite 创建vue3项目的详细流程](http://pic.xiahunao.cn/[vue3] 使用 vite 创建vue3项目的详细流程)
)







)


----快速移植FreeRTOS实战)


)

)
)