【数据结构】源码角度剖析PriorityQueue

认识 Queue

认识 PriorityQueue

PriorityQueue为什么要用二叉堆？

PriorityQueue构造方法源码分析

PriorityQueue 的属性

构造方法

JDK1.8传入不可比较的对象

JDK17传入不可比较的对象

传入带有Collection接口的对象

instanceof 关键字

Offer方法分析

JDK8Offer分析（传入可比较对象）

JDK17Offer分析（传入可比较对象）

JDK17Offer(手动传入比较器)

PriorityQueue 扩容机制

模拟堆操作

认识 Queue

Queue 是单端队列，只能从一端插入元素，另一端删除元素，实现上一般遵循 先进先出 规则。

下面我们看看常见的方法：

Queue 扩展了 Collection 的接口，根据 因为容量问题而导致操作失败后处理方式的不同 可以分为两类方法: 一种在操作失败后会抛出异常，另一种则会返回特殊值。

Queue接口	抛出异常	返回特殊值
插入队尾	add(E e)	offer(E e)
删除队首	remove()	poll()
查询队首元素	element()	peek()

认识 PriorityQueue

PriorityQueue是在 JDK1.5 中被引入的, 其与 Queue 的区别在于元素出队顺序是与优先级相关的，即总是优先级最高的元素先出队。

这里列举其相关的一些要点：

PriorityQueue 利用了二叉堆的数据结构来实现的，底层使用可变长的数组来存储数据
PriorityQueue 通过堆元素的上浮和下沉，实现了在 O(logn) 的时间复杂度内插入元素和删除堆顶元素。
PriorityQueue 是非线程安全的，且不支持存储 NULL（否则会抛出NullPointerException）和 non-comparable（否则会抛出 ClassCastException异常）的对象。
PriorityQueue 默认是小堆，但可以接收一个 Comparator 作为构造参数，从而来自定义元素优先级的先后。

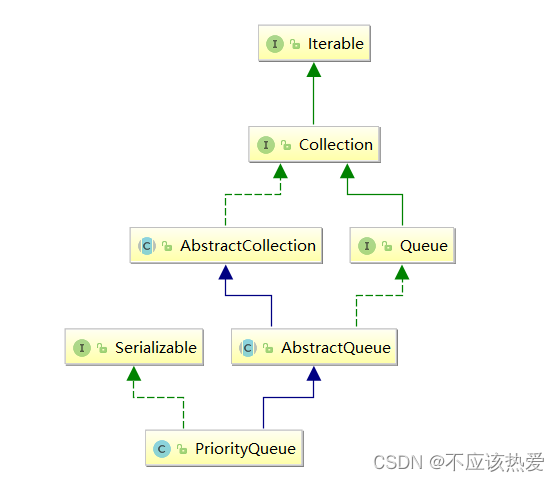
PriorityQueue为什么要用二叉堆？

PriorityQueue 选择使用二叉堆（Binary Heap）作为底层数据结构的原因主要是为了维护堆的性质，并保证一些基本操作的高效性能。二叉堆是一种特殊的完全二叉树，有两种类型：最小堆和最大堆。

以下是使用二叉堆的一些优势和原因：

高效的插入和删除操作： 二叉堆保持了堆的性质，使得插入和删除元素的操作非常高效。在最小堆中，堆顶元素是最小的，删除堆顶元素（poll操作）只需要常数时间，而插入元素也可以在对数时间内完成。
空间效率： 二叉堆可以使用数组实现，这样可以更有效地利用内存。相比于其他数据结构，它在实现上不需要额外的指针，而且数组的顺序存储有助于提高缓存命中率。
快速找到最小/最大元素： 在最小堆中，最小元素总是位于堆顶。在最大堆中，最大元素总是位于堆顶。这样，我们可以在常数时间内找到最小或最大元素。
适用于动态数据： 二叉堆对于动态数据集的管理非常有效，因为在插入和删除元素时，它能够在对数时间内维护堆的性质。

虽然二叉堆可能不是最适合所有情况的数据结构，但在某些场景下，特别是对于优先队列的实现，它提供了一种简单而高效的选择。注意，Java 中的 PriorityQueue 默认实现是最小堆，但可以通过提供自定义的比较器来实现最大堆。

PriorityQueue构造方法源码分析

就第三点：PriorityQueue 不支持存储 NULL（否则会抛出NullPointerException）和 non-comparable（否则会抛出 ff异常）的对象。

我们来看看源码：

PriorityQueue 的属性

下面为 PriorityQueue 的属性：（如想了解源码中的序列化和modCount相关知识，可移步博主另一篇博客ArrayList（源码分析））

    // 默认初始化大小private static final int DEFAULT_INITIAL_CAPACITY = 11;// 用数组实现的二叉堆，下面的英文注释确认了我们前面的说法。/*** Priority queue represented as a balanced binary heap: the two* children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The* priority queue is ordered by comparator, or by the elements'* natural ordering, if comparator is null: For each node n in the* heap and each descendant d of n, n <= d.  The element with the* lowest value is in queue[0], assuming the queue is nonempty.*/private transient Object[] queue ;// 队列的元素数量private int size = 0;// 比较器private final Comparator<? super E> comparator;// 修改版本private transient int modCount = 0;

构造方法

/*** 默认构造方法，使用默认的初始大小来构造一个优先队列，比较器comparator为空，这里要求入队的元素必须实现Comparator接口*/public PriorityQueue() {this(DEFAULT_INITIAL_CAPACITY, null);}/*** 使用指定的初始大小来构造一个优先队列，比较器comparator为空，这里要求入队的元素必须实现Comparator接口*/public PriorityQueue( int initialCapacity) {this(initialCapacity, null);}/*** 使用指定的初始大小和比较器来构造一个优先队列*/public PriorityQueue( int initialCapacity,Comparator<? super E> comparator) {// Note: This restriction of at least one is not actually needed,// but continues for 1.5 compatibility// 初始大小不允许小于1if (initialCapacity < 1)throw new IllegalArgumentException();// 使用指定初始大小创建数组this.queue = new Object[initialCapacity];// 初始化比较器this.comparator = comparator;}/*** 构造一个指定Collection集合参数的优先队列*/public PriorityQueue(Collection<? extends E> c) {// 从集合c中初始化数据到队列initFromCollection(c);// 如果集合c是包含比较器Comparator的(SortedSet/PriorityQueue)，则使用集合c的比较器来初始化队列的Comparatorif (c instanceof SortedSet)comparator = (Comparator<? super E>)((SortedSet<? extends E>)c).comparator();else if (c instanceof PriorityQueue)comparator = (Comparator<? super E>)((PriorityQueue<? extends E>)c).comparator();//  如果集合c没有包含比较器，则默认比较器Comparator为空else {comparator = null;// 调用heapify方法重新将数据调整为一个二叉堆heapify();}}/*** 构造一个指定PriorityQueue参数的优先队列*/public PriorityQueue(PriorityQueue<? extends E> c) {comparator = (Comparator<? super E>)c.comparator();initFromCollection(c);}/*** 构造一个指定SortedSet参数的优先队列*/public PriorityQueue(SortedSet<? extends E> c) {comparator = (Comparator<? super E>)c.comparator();initFromCollection(c);}/*** 从集合中初始化数据到队列*/private void initFromCollection(Collection<? extends E> c) {// 将集合Collection转换为数组aObject[] a = c.toArray();// If c.toArray incorrectly doesn't return Object[], copy it.// 如果转换后的数组a类型不是Object数组，则转换为Object数组if (a.getClass() != Object[].class)a = Arrays. copyOf(a, a.length, Object[]. class);// 将数组a赋值给队列的底层数组queuequeue = a;// 将队列的元素个数设置为数组a的长度size = a.length ;}

JDK1.8传入不可比较的对象

接下来我们先来看一组场景：在PriorityQueue中插入未提供排序方法的对象，以此来展示构造方法

JDK1.8：

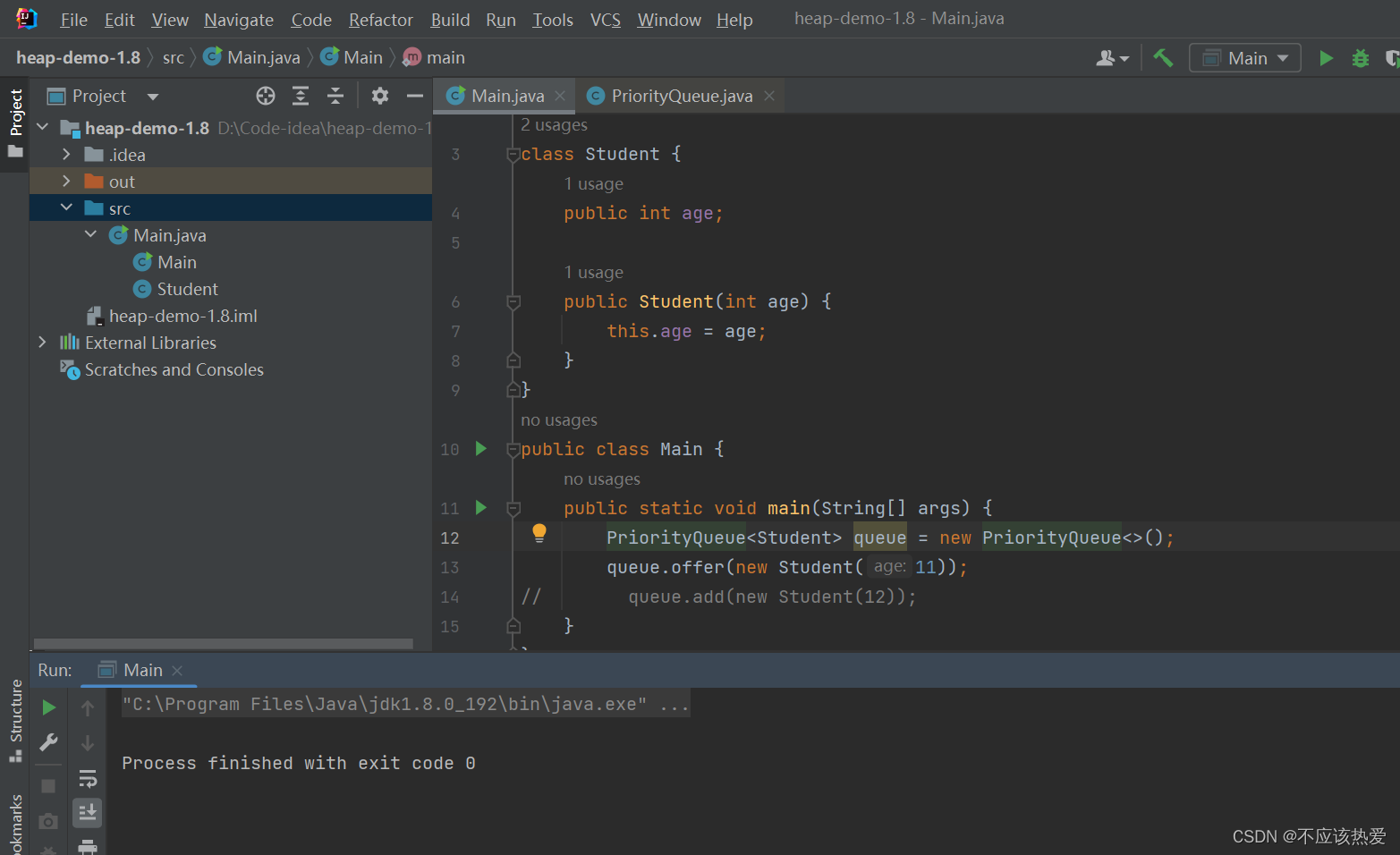
：第一次放入一个不可比较的对象不会报错，第二次时候才报错，原因下面讲解offer源码时候会解释。

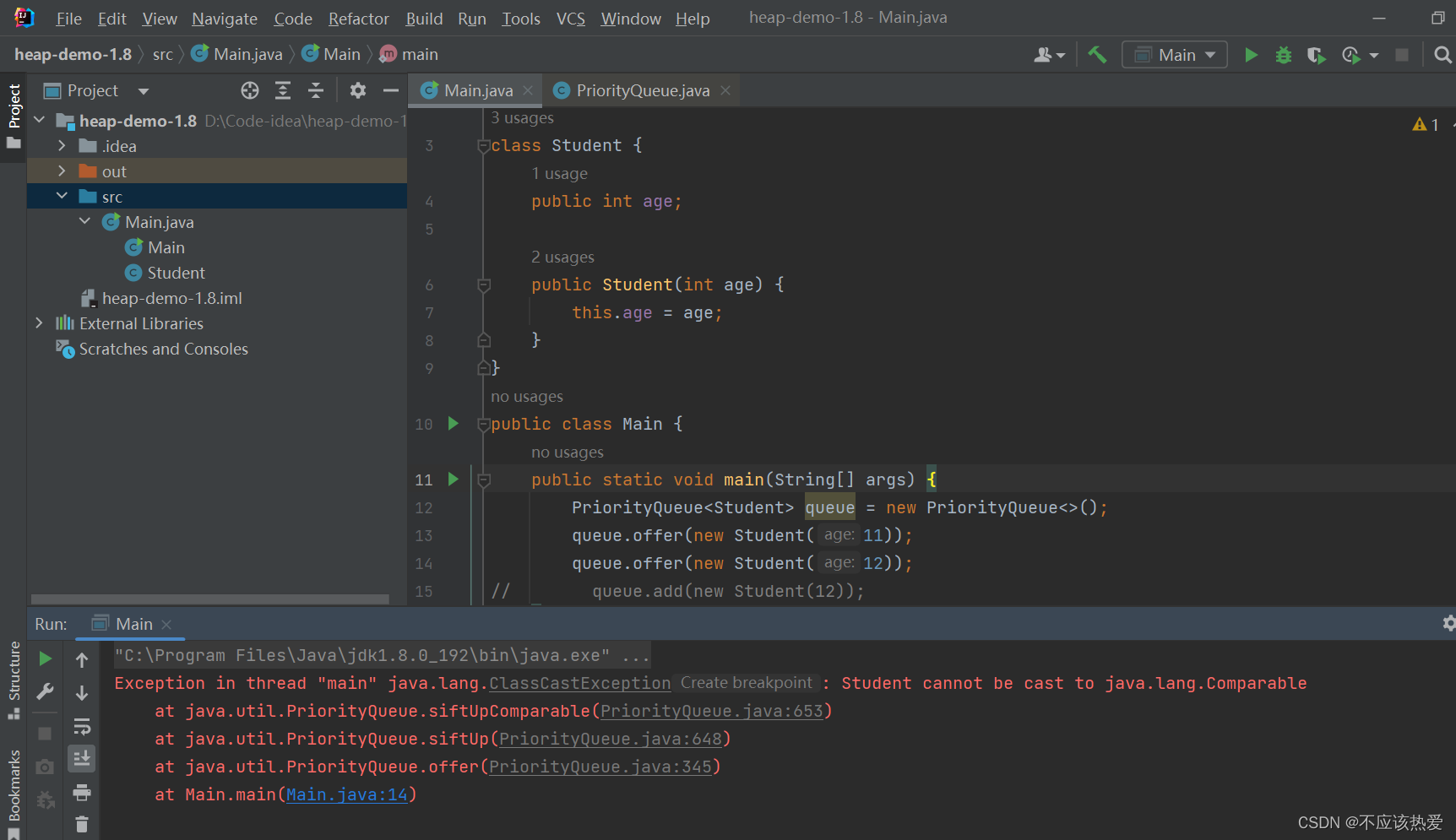
JDK17传入不可比较的对象

而JDK17（第一次放入一个不可比较的对象就立即报错）：

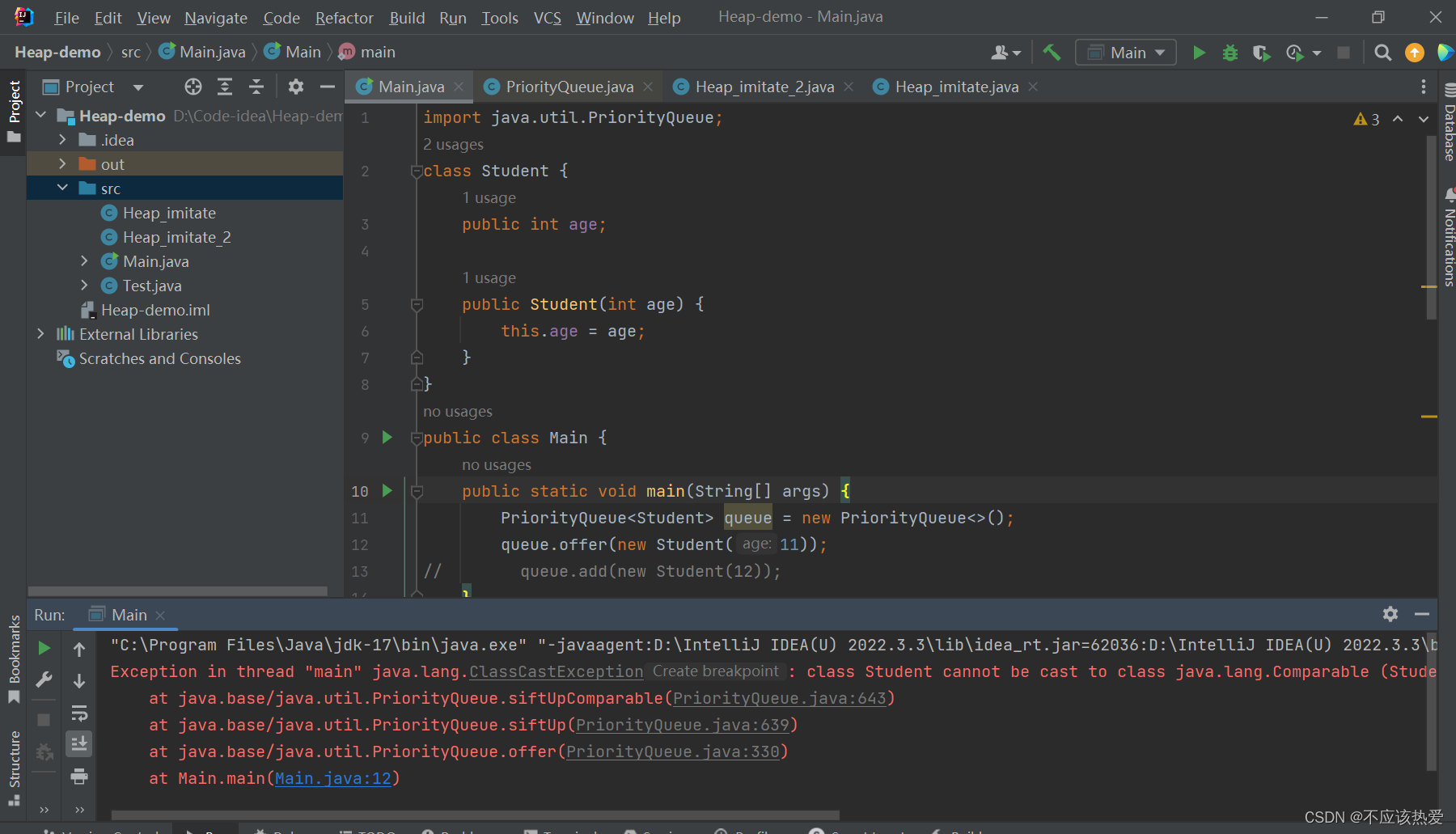
如果将Student实现Comparable接口就不会报错（以下均为JDK17实现）：

import java.util.PriorityQueue;
class Student implements Comparable<Student>{public int age;public Student(int age) {this.age = age;}@Overridepublic int compareTo(Student o) {return this.age - o.age;}
}
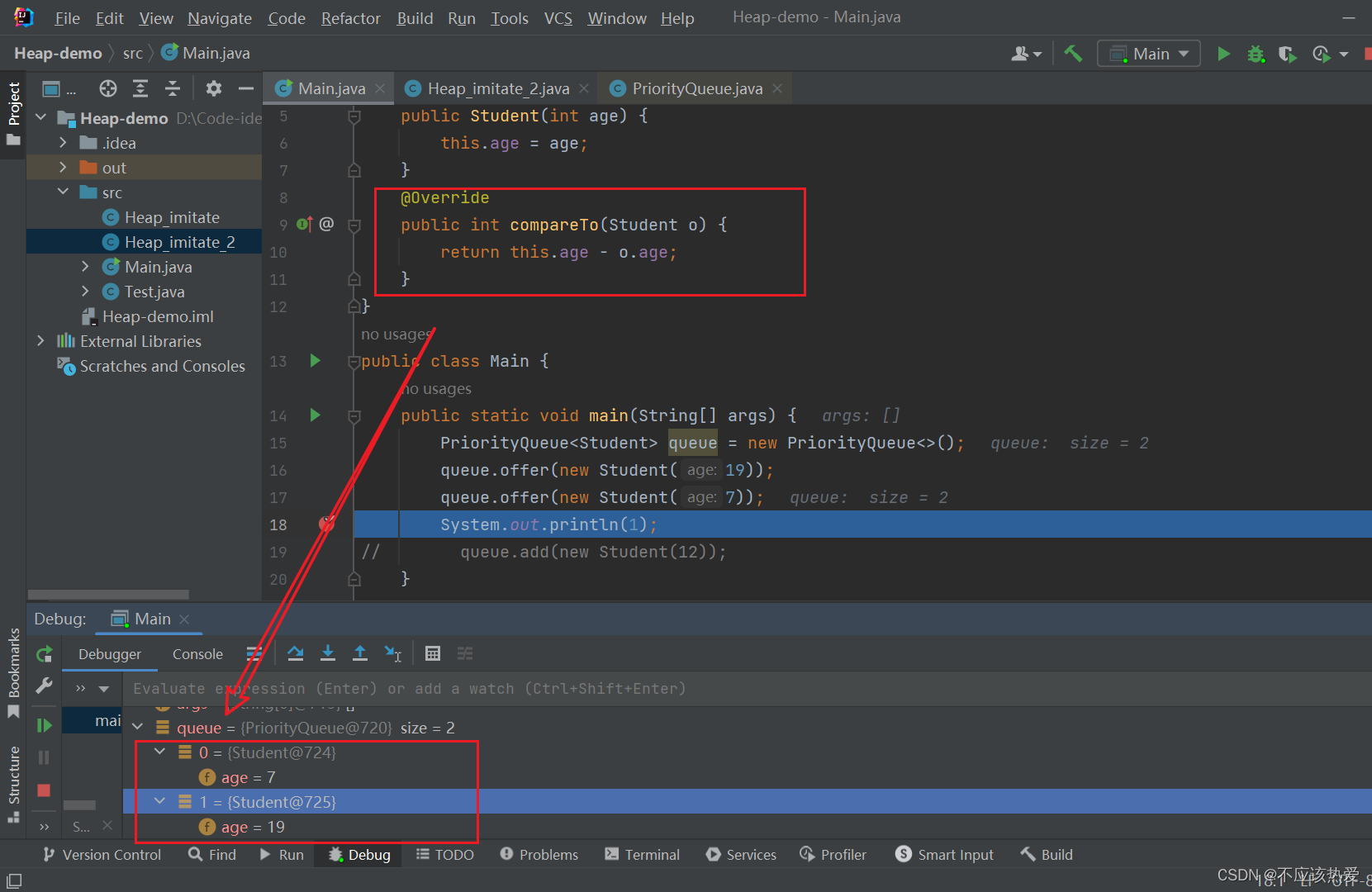
public class Main {public static void main(String[] args) {PriorityQueue<Student> queue = new PriorityQueue<>();queue.offer(new Student(11));queue.offer(new Student(7));System.out.println(1);
//        queue.add(new Student(12));}
}

运行结果：排序成功

传入带有Collection接口的对象

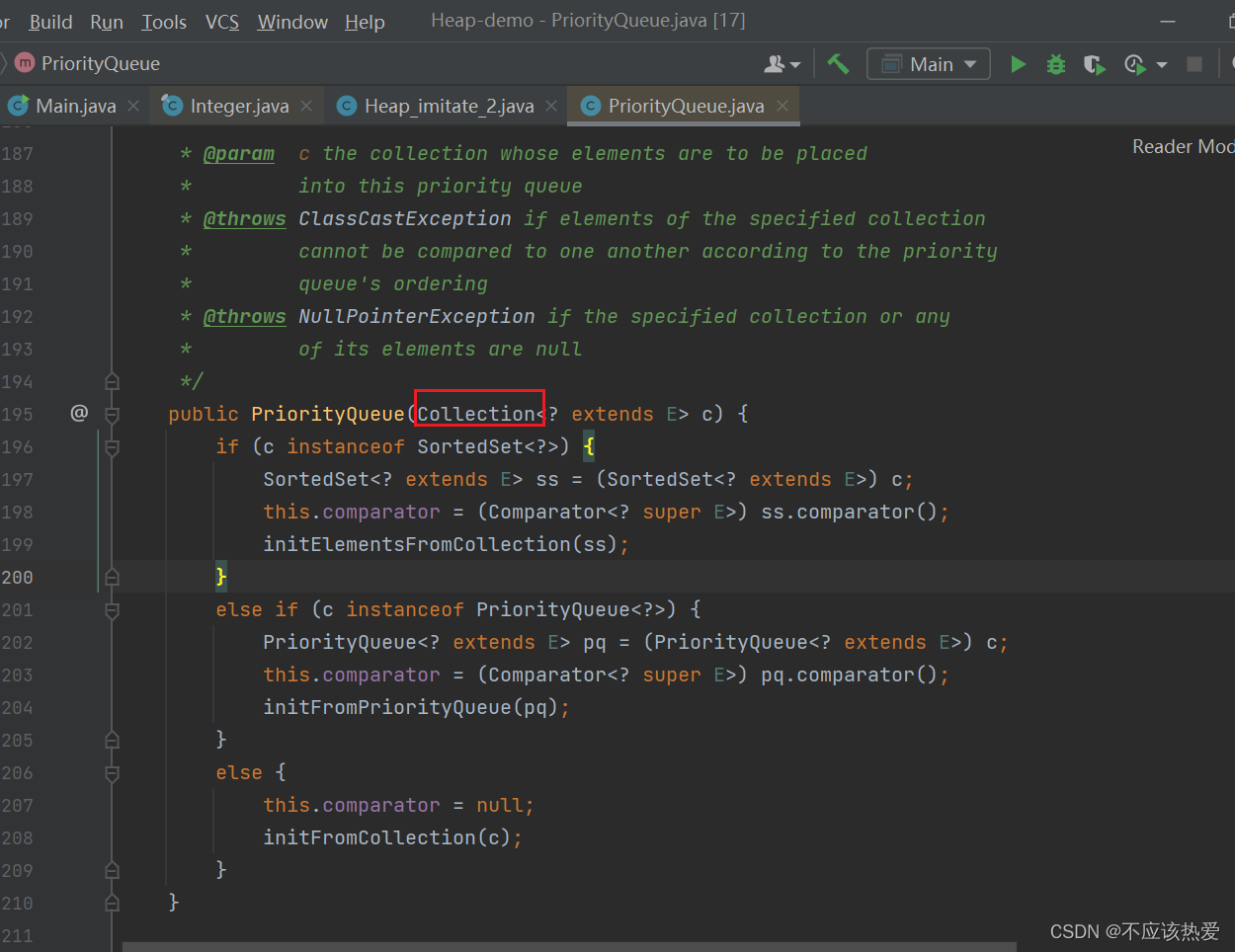
代码实现：

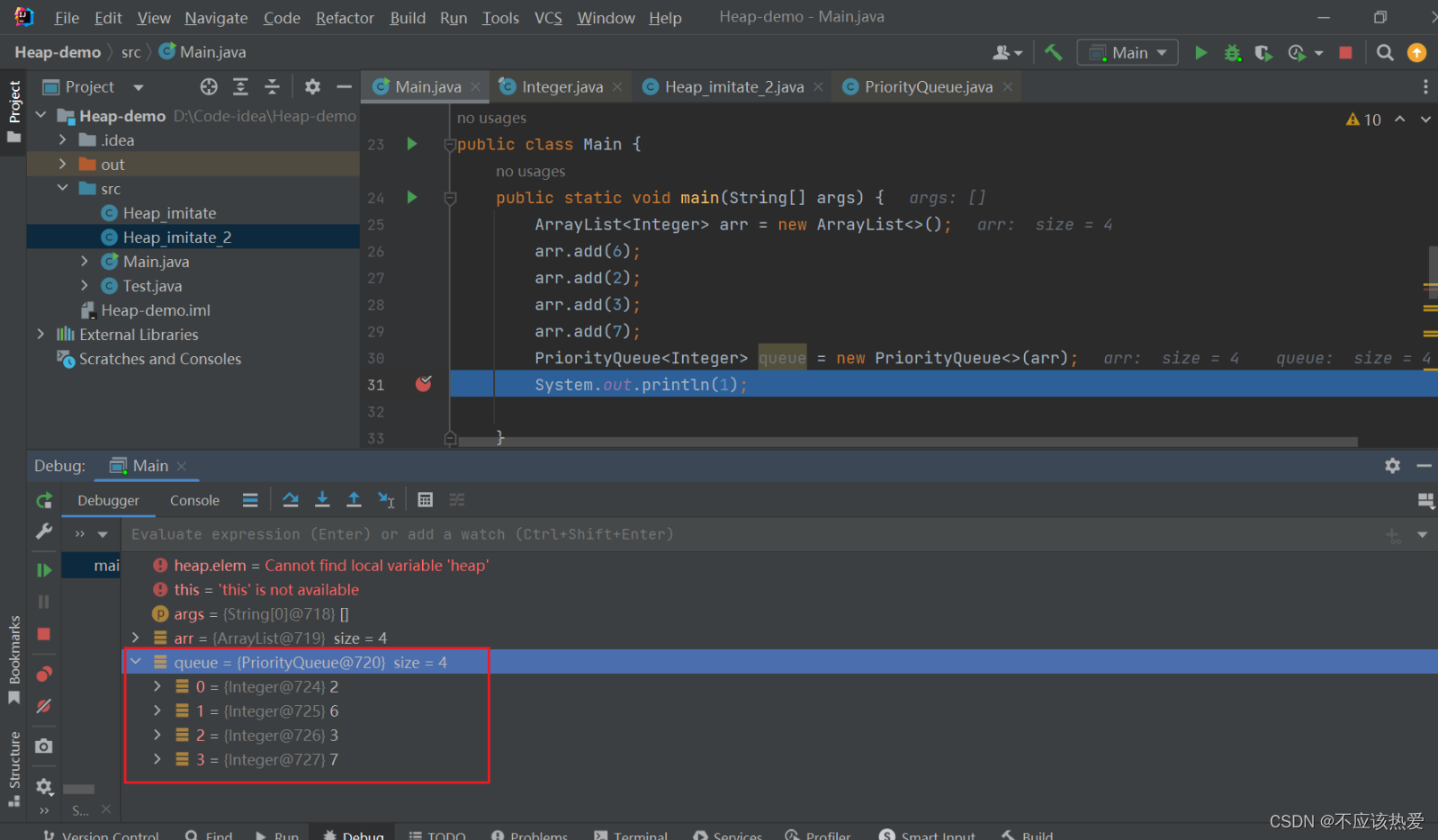
分析：ArrayList实现了Collection接口，所以可以直接进行排序（PriorityQueue 默认小根堆）。

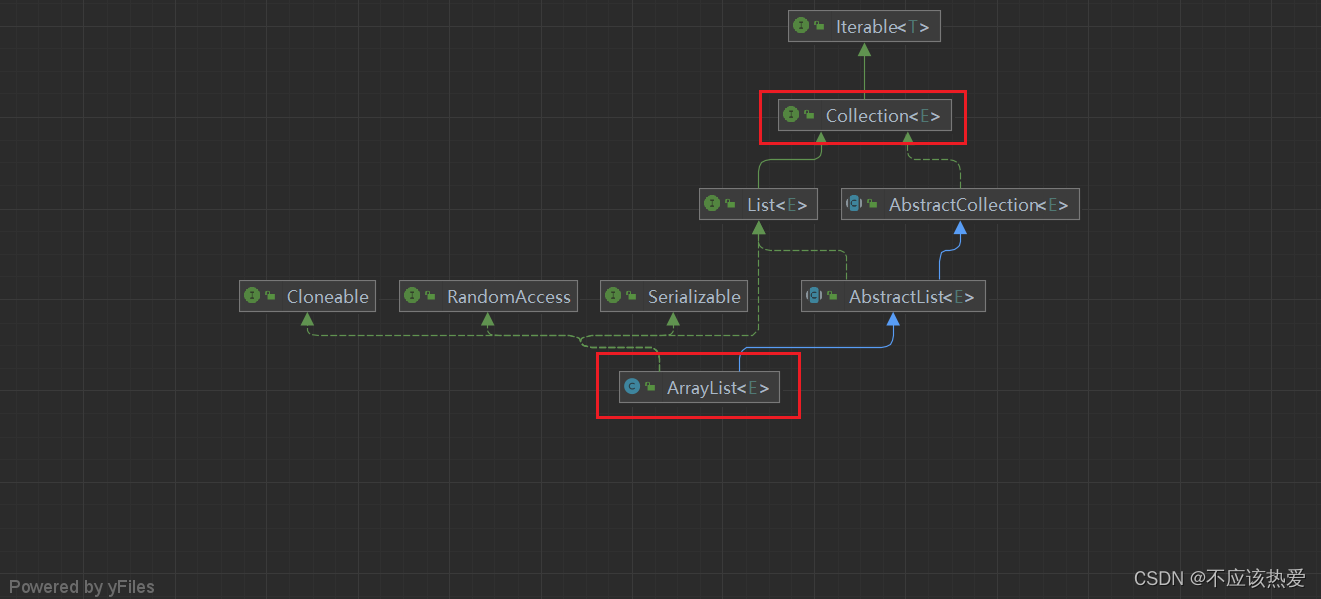
instanceof 关键字

instance of 是 Java 中的一个关键字，用于检查对象是否是某个类的实例，或者是否实现了某个接口。它的语法是：

object instanceof Class

其中，object 是一个对象，而 Class 是一个类名或接口名。instanceof 的结果是一个布尔值，如果 object 是 Class 的实例或者实现了 Class 接口，则结果为 true；否则，结果为 false。

例如，考虑以下代码：

List<String> myList = new ArrayList<>();
if (myList instanceof ArrayList) {System.out.println("myList is an instance of ArrayList");
} 
if (myList instanceof List) {System.out.println("myList is an instance of List");
}

在这个例子中，myList是 ArrayList 类型的实例，所以第一个条件为 true，而第二个条件也为 true，因为 ArrayList 是 List 接口的实现。因此，会输出两行信息。

Offer方法分析

分析以上场景所用到的构造方法：

第一次offer：new Student（11）；

当未给构造方法传入参数的时候，源码中会调用自身带有两个参数的构造方法，并设置数组的初始容量为11。

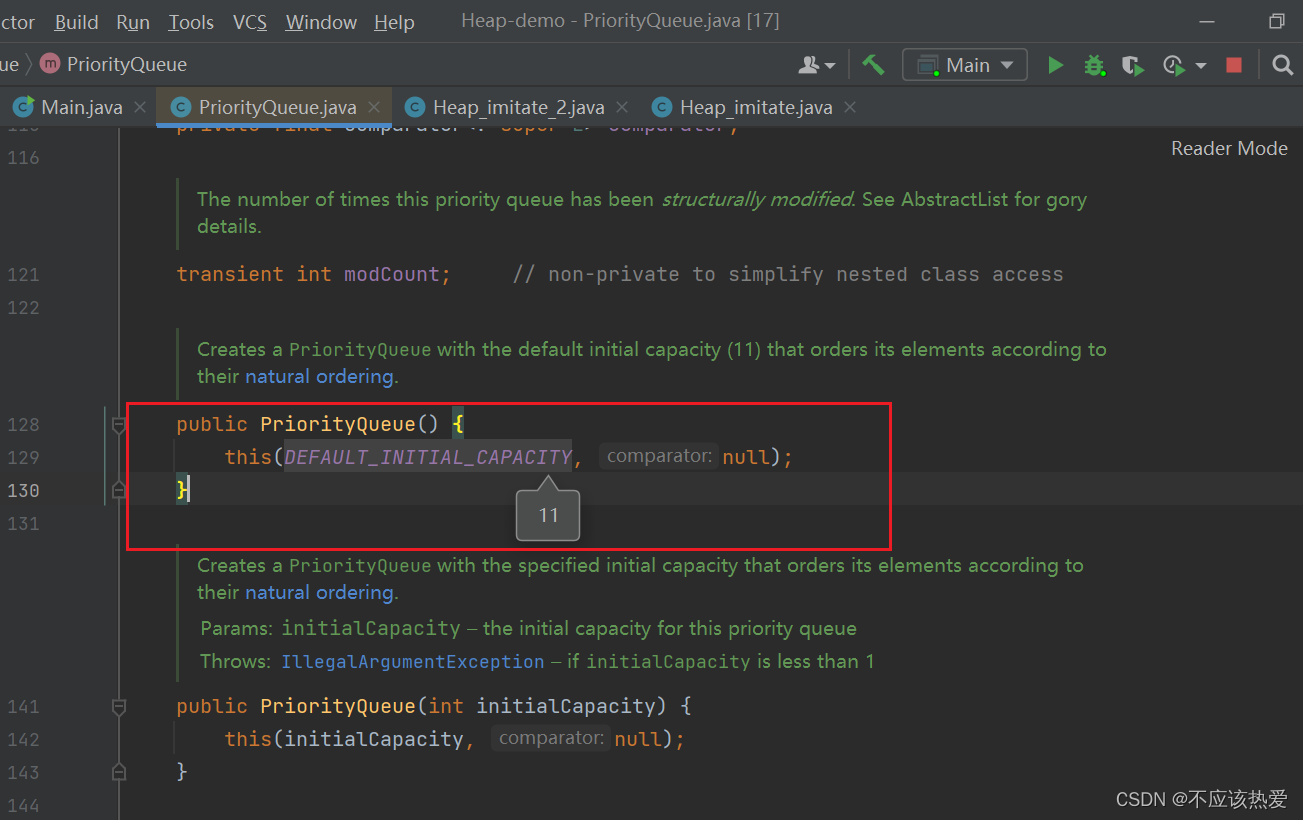
带有两个参数的构造方法如下：

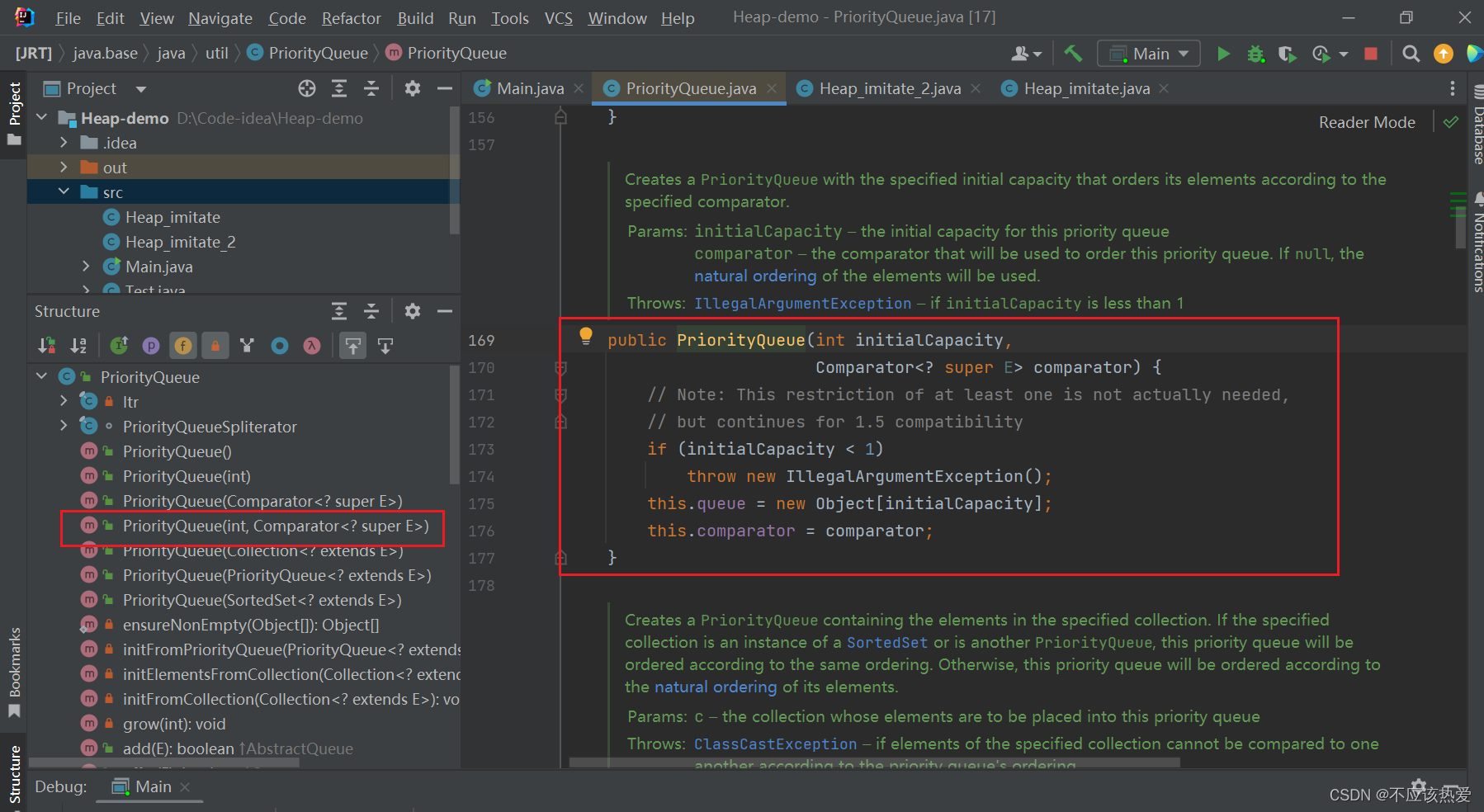
由于之前我们并未对构造方法传入比较器，所以这里的比较器为 null。容量为初始容量：11。

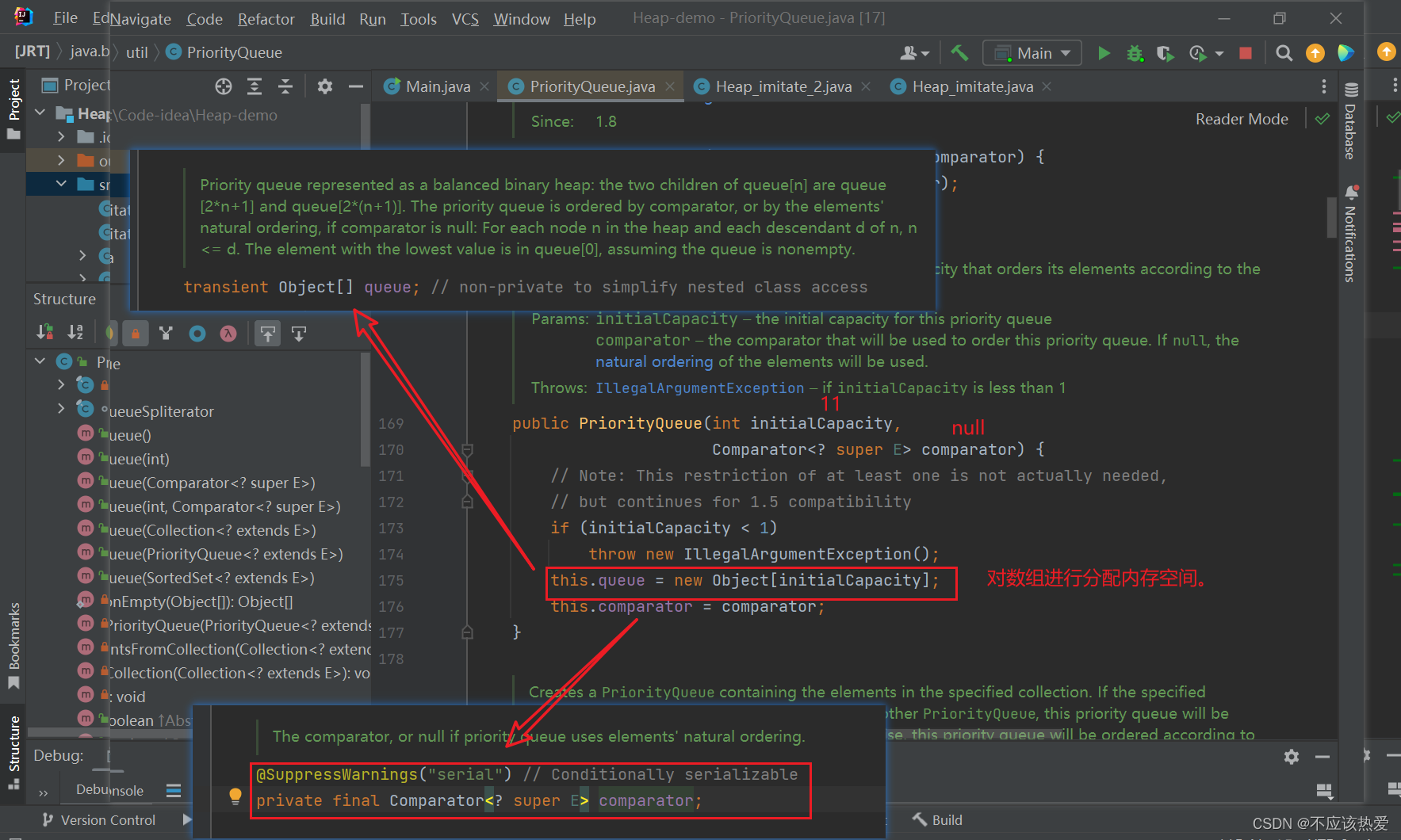
讲到这里：代码中，PriorityQueue<Student> queue = new PriorityQueue<>();所作的任务已经完成。

JDK8Offer分析（传入可比较对象）

下面我们来看看offer源码的实现：

（JDK8中的offer），这也是为什么我们前面第一次放入未实现Comparable接口的Student对象未报错：

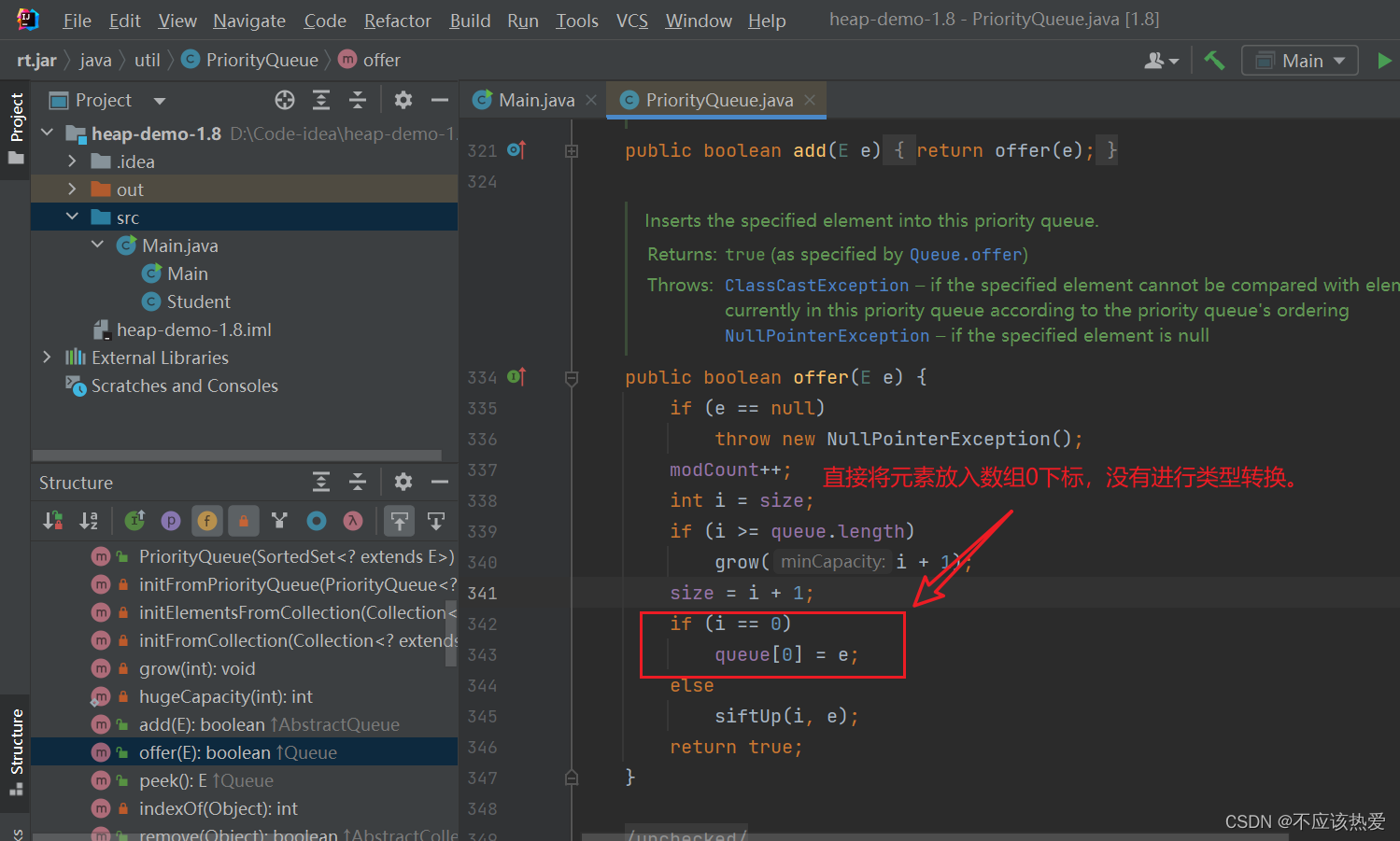
JDK17Offer分析（传入可比较对象）

JDK17源码：

无论是第几次放入元素，都会先进行类型转换（未传入比较器的情况下，如果传入对象未实现Compara接口，就会抛出异常——ClassCastException）。

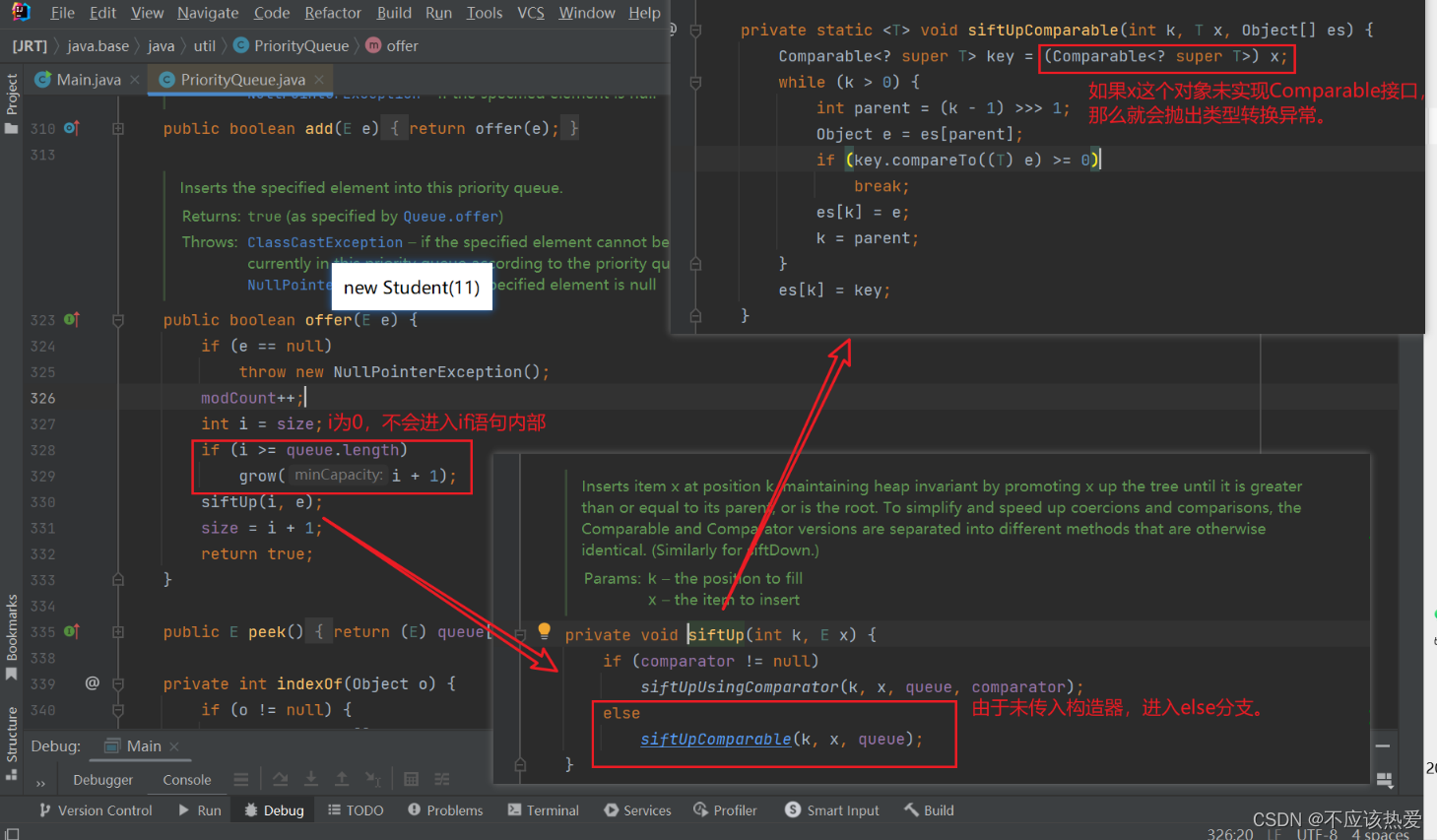
下面我们重点关注 siftUpComparable 方法的内部实现：

    private static <T> void siftUpComparable(int k, T x, Object[] es) {Comparable<? super T> key = (Comparable<? super T>) x;while (k > 0) {int parent = (k - 1) >>> 1;Object e = es[parent];if (key.compareTo((T) e) >= 0)break;es[k] = e;k = parent;}es[k] = key;}

图解分析：

可以看出JDK17，对类型检查更为严格。

第二次Offer操作：new Student(7)

以下为siftUpComparable的具体实现：

看到这里，我们知道，就可以通过我们自定义的compareTo方法来实现排序的顺序。

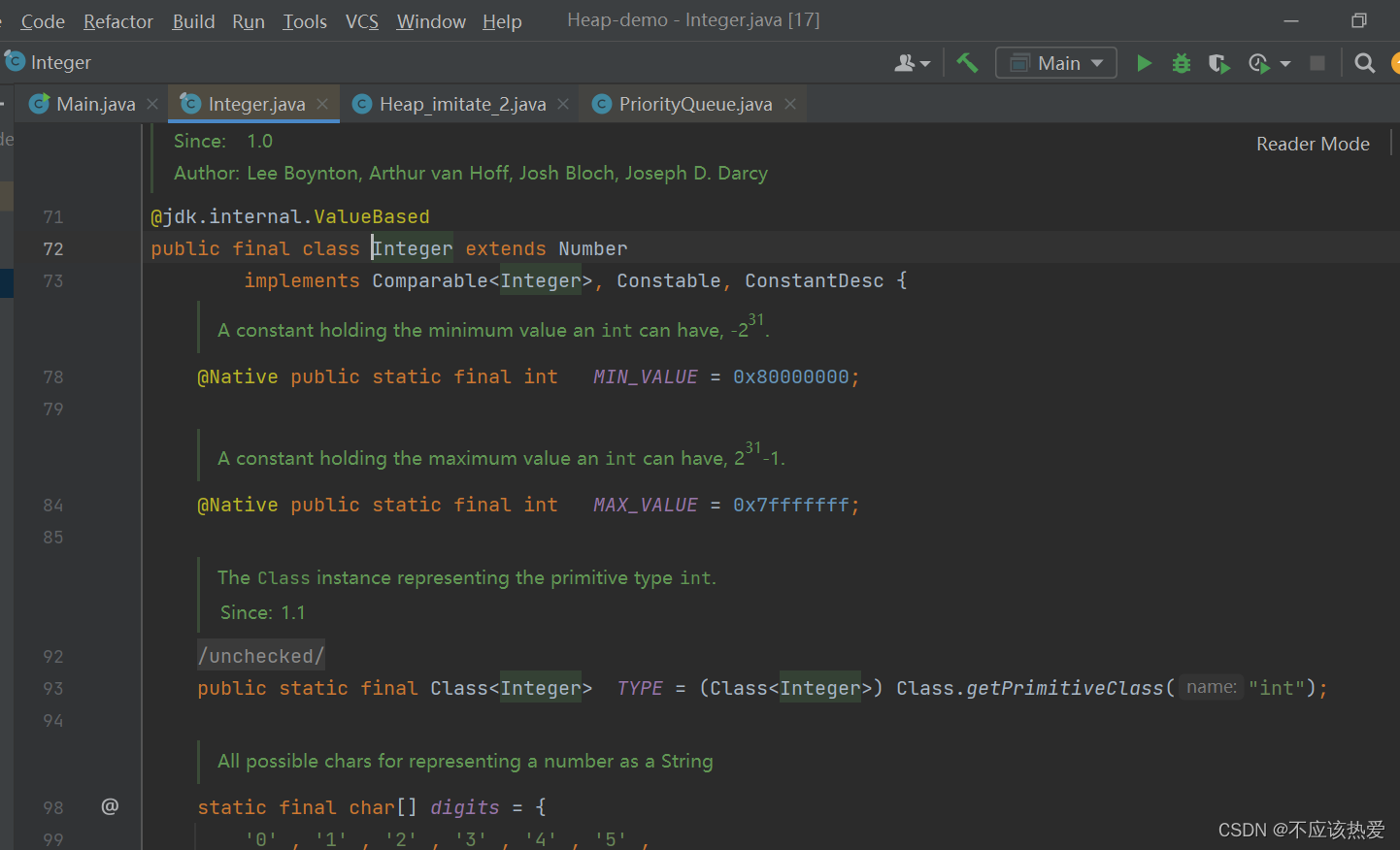
但是，如果我们传入的是整数呢？我们知道在进行offer操作的时候，整数会自动装箱成为Integer类型，但是我们不可能修改Integer的源码吧？

public class Main {public static void main(String[] args) {PriorityQueue<Integer> queue = new PriorityQueue<>();queue.offer(10);queue.offer(12);}
}

JDK17Offer(手动传入比较器)

因此这时候比较器就派上用场了：

class IntCom implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o1.compareTo(o2);}
}
public class Main {public static void main(String[] args) {PriorityQueue<Integer> queue = new PriorityQueue<>(new IntCom());queue.offer(19);queue.offer(12);}
}

接下来我们再来看看关于比较器的源码部分：

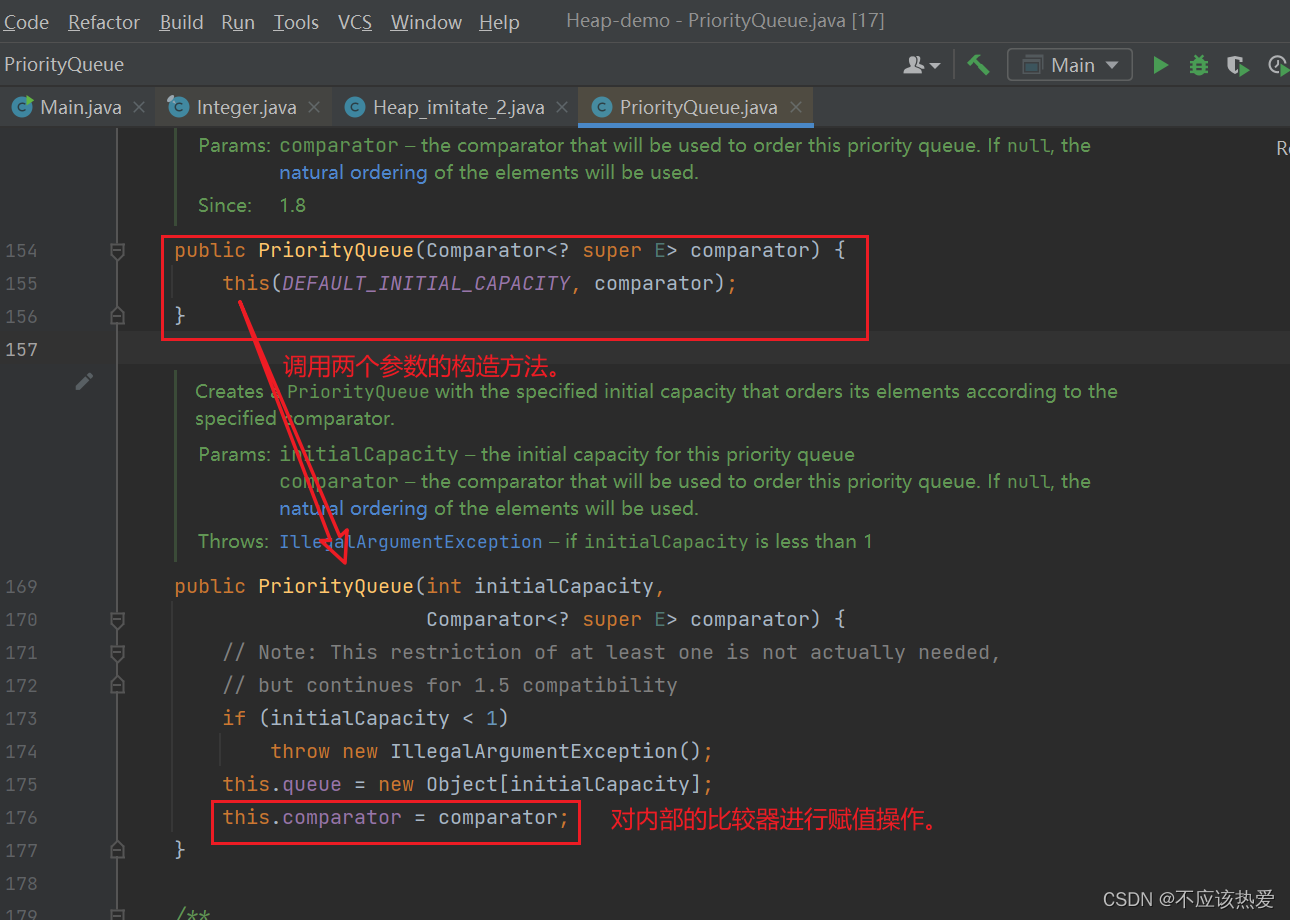
offer方法如下：

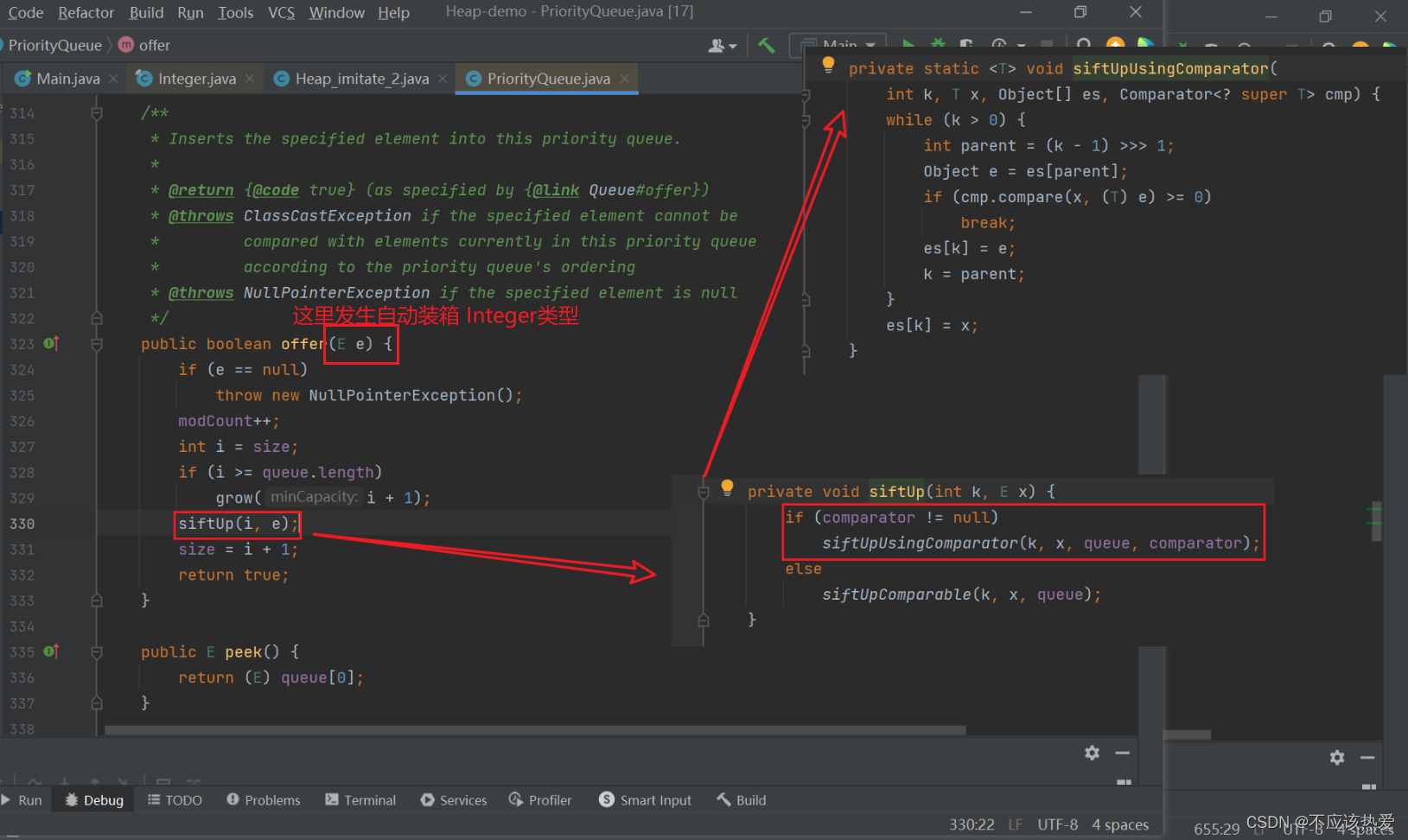
由于这里的siftUpUsingComparator部分与上面的传入带Comparable接口的对象差不多，这里就不作过多介绍。

PriorityQueue 扩容机制

模拟堆操作

import java.util.Arrays;public class Heap_imitate {public int[] elem;public int usedSize;//有效的数据个数public static final int DEFAULT_SIZE = 10;public Heap_imitate() {elem = new int[DEFAULT_SIZE];}public void initElem(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}/*** 时间复杂度：O(n)*/public void createHeap() {for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {//统一的调整方案shiftDown(parent,usedSize);}}/**** @param parent 每棵子树的根节点* @param len  每棵子树调整的结束位置 不能>len*             时间复杂度：O(log n)*/private void shiftDown(int parent,int len) {int child = 2*parent+1;//1. 必须保证有左孩子while (child < len) {//child+1 < len && 保证有右孩子if(child+1 < len && elem[child] < elem[child+1]) {child++;}//child下标 一定是左右孩子 最大值的下标/* if(elem[child] < elem[child+1] && child+1 < len ) {child++;}*/if(elem[child] > elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;parent = child;child = 2*parent+1;}else {break;}}}public void offer(int val) {if(isFull()) {//扩容elem = Arrays.copyOf(this.elem,2*this.elem.length);}this.elem[usedSize] = val;usedSize++;//想办法让他再次变成大根堆shiftUp(usedSize-1);}private void shiftUp(int child) {int parent = (child-1) / 2;while (child > 0) {//parent >= 0if (elem[child] > elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;child = parent;parent = (child-1)/2;}else {break;}}}public boolean isFull() {return usedSize == elem.length;}public int pop() {if(isEmpty()) {return -1;}int tmp = elem[0];elem[0] = elem[usedSize-1];elem[usedSize-1] = tmp;usedSize--;//保证他仍然是一棵大根堆shiftDown(0,usedSize);return tmp;}public boolean isEmpty() {return usedSize == 0;}public int peek() {if(isEmpty()) {return -1;}return elem[0];}/*** 时间复杂度：*  O(n) + O(n*logn) 约等于 O(nlogn)*  空间复杂度：O(1)*/public void heapSort() {//1.建立大根堆 O(n)createHeap();//2.然后排序int end = usedSize-1;while (end > 0) {int tmp = elem[0];elem[0] = elem[end];elem[end] = tmp;shiftDown(0,end);end--;}}}