一、概要
随着联邦学习的发展,简单的聚合算法已经不在有效。但复杂的聚合算法使得联邦学习训练时间出现新的瓶颈。本文提出了并行联邦学习(parallel federated learning,PFL),通过调换中心节点聚合和广播的顺序。本文算法的优点:在全局聚合计算时解锁了边缘节点,在边缘节点本地计算时解锁了中心节点,并且在计算过程中具有灵活的伸缩性。
本文主要贡献:
- 处理数据异构和网络掉队
- 局部节点参与灵活性
- 计算训练过程中的可扩展性
二、关键算法
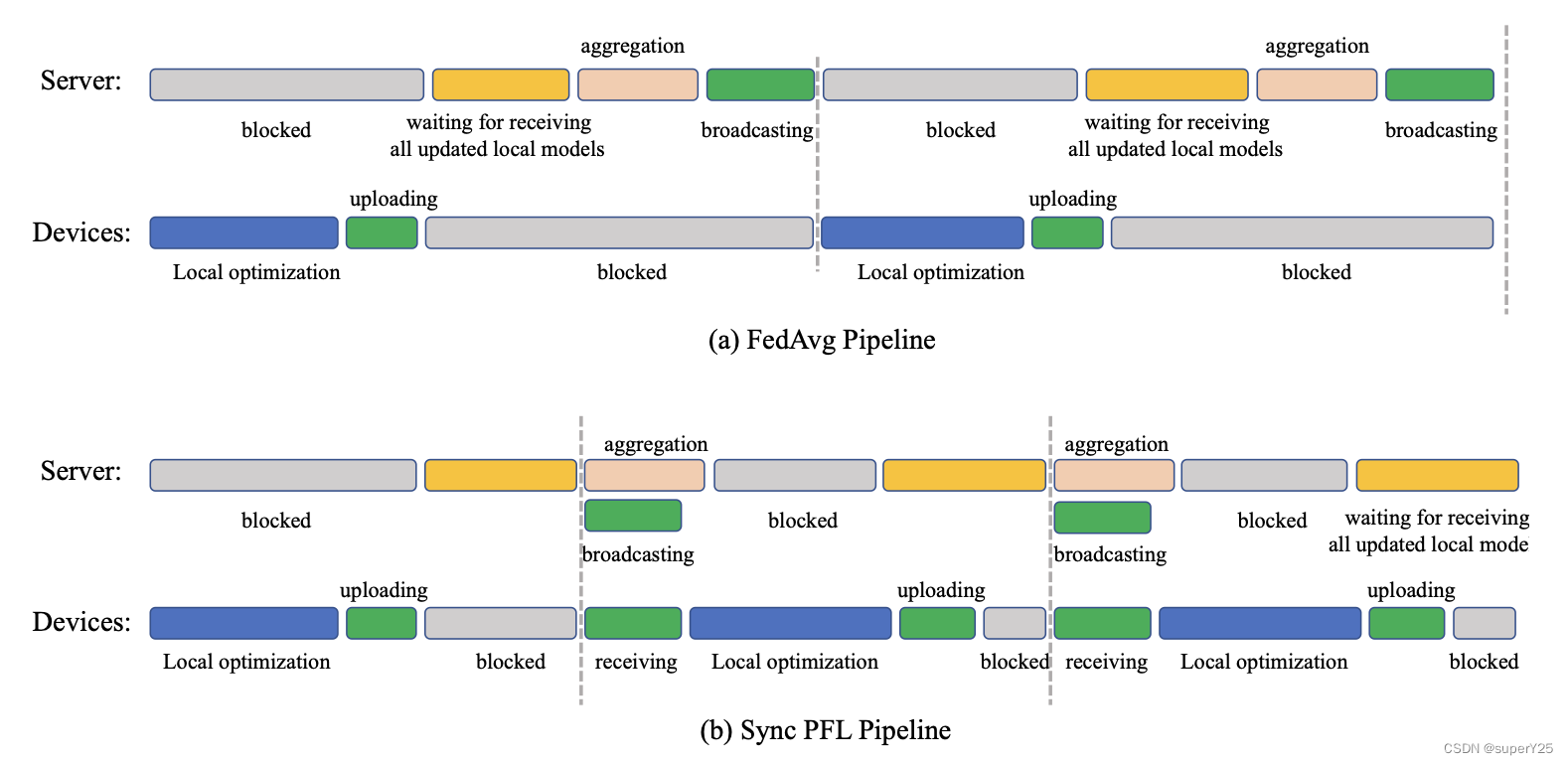
本文的PFL算法并没有重新设计FL框架,仅仅只是将原计算流程进行了适当的调整,主要包含同步的SPFL和异步的APFL。如图所示,(a)表示FedAvg流程:uploading–>global aggregation–>broadcasting–>local optimization。(b)表示本文提出的SPFL流程:uploading(中心节点接收当前所有边缘局部更新)–>broadcasting(中心节点广播缓存中的全局模型参数)–>全局聚合计算(中心节点利用接收到的局部更新聚合全局模型参数)。该设计可以使得本地一旦优化完成便上传到中心节点,而中心节点一旦接收到本地更新边广播缓存中的全局模型参数。因此边缘节点和中心节点不用等待阻塞。
下图是APFL的流程图:

SPFL
同步的PFL并不能处理网络掉队的问题,而是对复杂聚合逻辑做了相应的处理。其流程中对应的处理逻辑分别如下:
- Local Update:边缘节点接收全局模型参数 w t − 1 ( g ) w_{t-1}^{(g)} wt−1(g),然后使用SGD算法更新本地模型,公式: w t ( i ) = w t − 1 ( g ) − γ G t − 1 ( i ) w_{t}^{(i)} = w_{t-1}^{(g)} - \gamma G_{t-1}^{(i)} wt(i)=wt−1(g)−γGt−1(i),其中 t t t为训练轮数, i i i为第 i i i各节点, w t − 1 ( g ) w_{t-1}^{(g)} wt−1(g)为 t − 1 t-1 t−1轮时的全局模型, G t − 1 ( i ) G_{t-1}^{(i)} Gt−1(i)为通过 w t − 1 ( g ) w_{t-1}^{(g)} wt−1(g)计算得到的梯度。
- Uploading:一旦本地模型训练完成,便计算 δ ( i ) \delta^{(i)} δ(i)并上传到中心节点。
- Broadcasting:中心节点接收到所有边缘节点的 { δ ( i ) } i = 1 N \{\delta^{(i)}\}_{i=1}^{N} {δ(i)}i=1N,便将缓存中上一轮的聚合结果 w t − 1 ( g ) w_{t-1}^{(g)} wt−1(g)广播给边缘节点。这里如果上一轮的聚合结果没有完成,将会阻塞等待其完成。
- Global Aggregation:一旦广播成功,中心节点便执行下一轮的聚合计算: w t + 1 ( g ) = w t ( g ) + 1 N ∑ i = 1 N δ ( i ) w_{t+1}^{(g)}=w_{t}^{(g)}+\frac{1}{N}\sum_{i=1}^N \delta^{(i)} wt+1(g)=wt(g)+N1∑i=1Nδ(i)
APFL
异步的PFL同时对边缘节点的网络掉队问题和中心节点的复杂聚合算法逻辑做了优化。每个边缘节点和中心节点都有不同的clocks,并且中心节点的clock只和其中一个边缘节点有关,例如对于第 t t t个中心节点的clock,APFL的流程如下:
- Local Update:边缘节点 i i i完成和中心节点的通信,并接收到全局模型 w t − 1 ( g ) w_{t-1}^{(g)} wt−1(g),然后更新本地模型: w t ( i ) = w t − 1 ( g ) − γ G t − 1 ( i ) w_{t}^{(i)} = w_{t-1}^{(g)} - \gamma G_{t-1}^{(i)} wt(i)=wt−1(g)−γGt−1(i)。
- Uploading:完成本地模型更新之后,上传本地梯度 δ ( i ) \delta^{(i)} δ(i),在边缘节点 i i i本地训练和梯度上传过程中,有 n n n个其他边缘节点和中心节点通信。因此,当中心节点接收到边缘节点 i i i的本地更新之后,中心节点的clock已经是 t + n + 1 t+n+1 t+n+1了
- Broadcasting:中心节点在接收到边缘节点 i i i的本地更新 δ ( i ) \delta^{(i)} δ(i)后,将缓存中最新的全局模型发送给边缘节点 i i i,这里的最新全局模型可能是 w t + n ( g ) w_{t+n}^{(g)} wt+n(g),也可能是 w t + n − r ( g ) w_{t+n-r}^{(g)} wt+n−r(g),表示中心节点在clock t t t到clock t + n t+n t+n中任意clock聚合得到的结果。
- Global Aggregation:中心节点在上一轮聚合过程中,会接收到一部分边缘节点上传的 δ ( i ) \delta^{(i)} δ(i)。因此,聚合计算: w t + n + 1 ( g ) = w t + n + 1 − p ( g ) + 1 N ∑ i = 1 C t δ ( i ) w_{t+n+1}^{(g)}=w_{t+n+1-p}^{(g)}+\frac{1}{N}\sum_{i=1}^{C_t} \delta^{(i)} wt+n+1(g)=wt+n+1−p(g)+N1∑i=1Ctδ(i),其中 C t C_t Ct表示中心节点接收的 δ ( i ) \delta^{(i)} δ(i)的数据量, p p p属于 C t C_t Ct。通常 C t C_t Ct只包含一个边缘节点。
SPFL和APFL的异同
-
SPFL的中心节点更新 w w w时需要等待所有边缘节点的上传,APFL不需要。
-
SPFL和APFL相比普通的FL有不同的加速。

-
SPFL和APFL的收敛分析中,都能有不错的收敛。(很多数学上的分析,可以移步论文)
三、总结
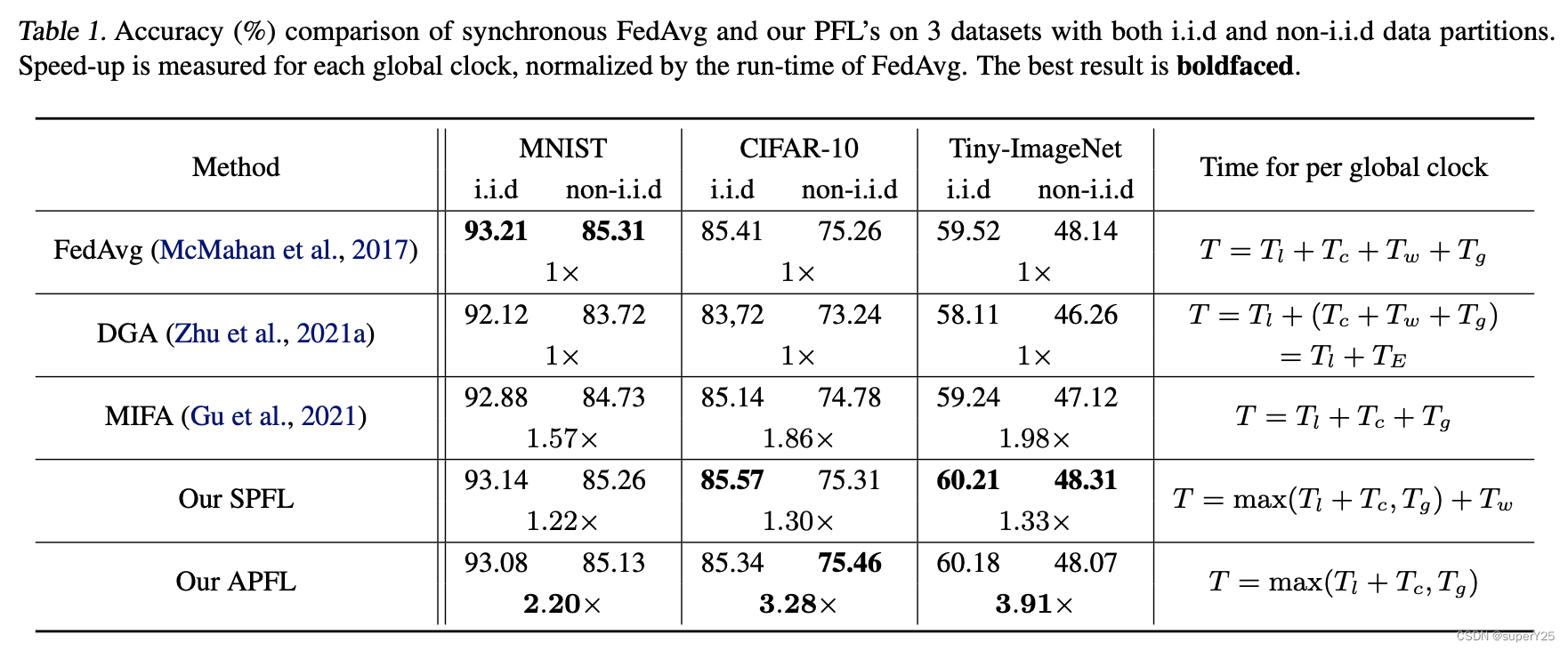
从实验结果看,本文提出的算法对中心节点场景的模型训练加速优化具有很好的参考意义。

论文地址:点这里







--实战一下)









)

