第一题:分蛋糕
小明今天生日,他有 n 块蛋糕要分给朋友们吃,这 n 块蛋糕(编号为 1 到 n)的重量分别为 a1,a2,…,an。
小明想分给每个朋友至少重量为 k 的蛋糕。
小明的朋友们已经排好队准备领蛋糕,对于每个朋友,小明总是先将自己手中编号最小的蛋糕分给他,当这个朋友所分得蛋糕的重量不到 k 时,再继续将剩下的蛋糕中编号最小的给他,直到小明的蛋糕分完或者这个朋友分到的蛋糕的总重量大于等于 k。
请问当小明的蛋糕分完时,总共有多少个朋友分到了蛋糕。
输入格式
输入的第一行包含了两个整数 n,k,意义如上所述。
第二行包含 n 个正整数,依次表示 a1,a2,…,an。
输出格式
输出一个整数,表示有多少个朋友分到了蛋糕。
数据范围
对于所有评测用例,1≤n≤1000,1≤k≤10000,1≤ai≤1000。
输入样例:
6 9 2 6 5 6 3 5输出样例:
3样例解释
第一个朋友分到了前 3 块蛋糕,第二个朋友分到了第 4、5 块蛋糕,第三个朋友分到了最后一块蛋糕。
解题思路:
计算每一个区间如果该区间的和大于了给定范围,答案加一,最终输出答案即可。
#include<iostream>
#include<algorithm>using namespace std;const int N = 1010;
int n , m;
int a[N];int main()
{cin >> n >> m;for(int i = 0;i < n;i ++)cin >> a[i];int res = 0;int temp = 0;for(int i = 0;i < n;i ++){temp += a[i];if(temp >= m) res ++ , temp = 0;}if(temp) res ++;cout << res << endl;return 0;
}第二题:学生排队
体育老师小明要将自己班上的学生按顺序排队。
他首先让学生按学号从小到大的顺序排成一排,学号小的排在前面,然后进行多次调整。
一次调整小明可能让一位同学出队,向前或者向后移动一段距离后再插入队列。
例如,下面给出了一组移动的例子,例子中学生的人数为 8 人。
- 初始队列中学生的学号依次为 1,2,3,4,5,6,7,8;
- 第一次调整,命令为“3 号同学向后移动 2”,表示 3 号同学出队,向后移动 2 名同学的距离,再插入到队列中,新队列中学生的学号依次为 1,2,4,5,3,6,7,8;
- 第二次调整,命令为“8 号同学向前移动 3”,表示 8 号同学出队,向前移动 3 名同学的距离,再插入到队列中,新队列中学生的学号依次为 1,2,4,5,8,3,6,7;
- 第三次调整,命令为“3 号同学向前移动 2”,表示 3 号同学出队,向前移动 2 名同学的距离,再插入到队列中,新队列中学生的学号依次为 1,2,4,3,5,8,6,7。
小明记录了所有调整的过程,请问,最终从前向后所有学生的学号依次是多少?
请特别注意,上述移动过程中所涉及的号码指的是学号,而不是在队伍中的位置。
在向后移动时,移动的距离不超过对应同学后面的人数,如果向后移动的距离正好等于对应同学后面的人数则该同学会移动到队列的最后面。
在向前移动时,移动的距离不超过对应同学前面的人数,如果向前移动的距离正好等于对应同学前面的人数则该同学会移动到队列的最前面。
输入格式
输入的第一行包含一个整数 n,表示学生的数量,学生的学号由 1 到 n 编号。
第二行包含一个整数 m,表示调整的次数。
接下来 m 行,每行两个整数 p,q,如果 q 为正,表示学号为 p 的同学向后移动 q,如果 q 为负,表示学号为 p 的同学向前移动 −q。
输出格式
输出一行,包含 n 个整数,相邻两个整数之间由一个空格分隔,表示最终从前向后所有学生的学号。
数据范围
对于所有评测用例,1≤n≤1000,1≤m≤1000,所有移动均合法。
输入样例:
8 3 3 2 8 -3 3 -2输出样例:
1 2 4 3 5 8 6 7
解题思路:
模拟每一次出队和进队的操作。
向后移动k位就是当前元素向后交换k位。
向前移动k位就是当前元素向前交换k位。
#include<iostream>
#include<vector>using namespace std;const int N = 1010;
int n;
int t;
int w[N];int main()
{cin >> n >> t;for(int i = 1;i <= n;i ++) w[i] = i;while(t --){int a , b;cin >> a >> b;int idx;for(int i = 1;i <= n;i ++)if(w[i] == a) idx = i;if(b > 0){// 向后移动k位,即将当前位置的元素向后交换k次for(int i = 0;i < b;i ++)swap(w[idx + i] , w[idx + i + 1]);}else {// 向前移动k位,即将当前位置的元素向前交换k次b = -b;for(int i = 0;i < b;i ++)swap(w[idx - i] , w[idx - i - 1]);}}for(int i = 1;i <= n;i ++)cout << w[i] << " ";return 0;
}第三题:Markdown
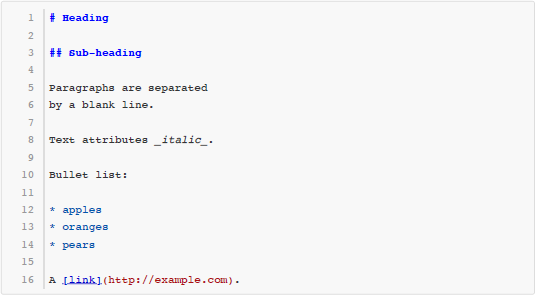
Markdown 是一种很流行的轻量级标记语言(lightweight markup language),广泛用于撰写带格式的文档。
例如以下这段文本就是用 Markdown 的语法写成的:
这些用 Markdown 写成的文本,尽管本身是纯文本格式,然而读者可以很容易地看出它的文档结构。
同时,还有很多工具可以自动把 Markdown 文本转换成 HTML 甚至 Word、PDF 等格式,取得更好的排版效果。
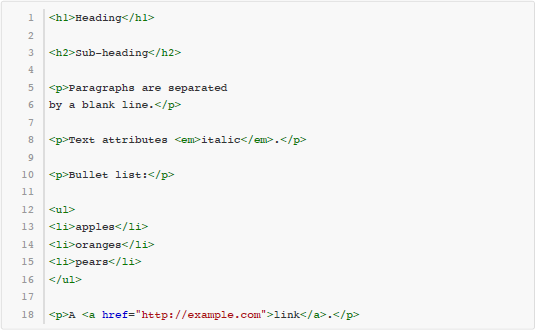
例如上面这段文本通过转化得到的 HTML 代码如下所示:
本题要求由你来编写一个 Markdown 的转换工具,完成 Markdown 文本到 HTML 代码的转换工作。
简化起见,本题定义的 Markdown 语法规则和转换规则描述如下:
●区块:区块是文档的顶级结构。本题的 Markdown 语法有 3 种区块格式。在输入中,相邻两个区块之间用一个或多个空行分隔。输出时删除所有分隔区块的空行。
○段落:一般情况下,连续多行输入构成一个段落。段落的转换规则是在段落的第一行行首插入<p>,在最后一行行末插入</p>。
○标题:每个标题区块只有一行,由若干个#开头,接着一个或多个空格,然后是标题内容,直到行末。#的个数决定了标题的等级。转换时,# Heading转换为<h1>Heading</h1>,## Heading转换为<h2>Heading</h2>,以此类推。标题等级最深为 6。
○无序列表:无序列表由若干行组成,每行由*开头,接着一个或多个空格,然后是列表项目的文字,直到行末。转换时,在最开始插入一行<ul>,最后插入一行</ul>;对于每行,* Item转换为<li>Item</li>。本题中的无序列表只有一层,不会出现缩进的情况。
●行内:对于区块中的内容,有以下两种行内结构。
○强调:_Text_转换为<em>Text</em>。强调不会出现嵌套,每行中_的个数一定是偶数,且不会连续相邻。注意_Text_的前后不一定是空格字符。
○超级链接:[Text](Link)转换为<a href="Link">Text</a>。超级链接和强调可以相互嵌套,但每种格式不会超过一层。输入格式
输入由若干行组成,表示一个用本题规定的 Markdown 语法撰写的文档。
输出格式
输出由若干行组成,表示输入的 Markdown 文档转换成产生的 HTML 代码。
数据范围
本题的测试点满足以下条件:
- 本题每个测试点的输入数据所包含的行数都不超过 100,每行字符的个数(包括行末换行符)都不超过 100。
- 除了换行符之外,所有字符都是 ASCII 码 32 至 126 的可打印字符。
- 每行行首和行末都不会出现空格字符。
- 输入数据除了 Markdown 语法所需,内容中不会出现
#、*、_、[、]、(、)、<、>、&这些字符。- 所有测试点均符合题目所规定的 Markdown 语法,你的程序不需要考虑语法错误的情况。
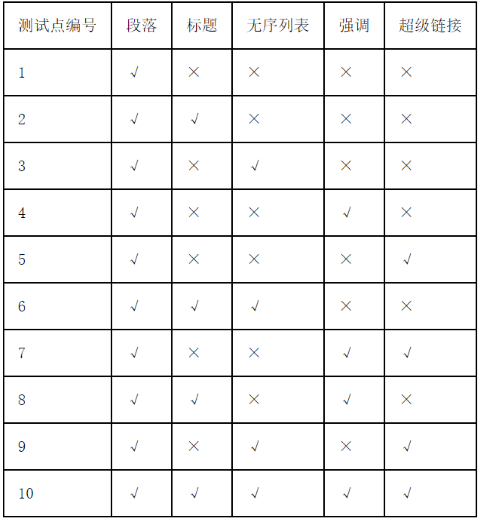
每个测试点包含的语法规则如下表所示,其中“√”表示包含,“×”表示不包含。
输入样例:
# HelloHello, world!输出样例:
<h1>Hello</h1> <p>Hello, world!</p>
解题思路:
超级大模拟,只会写区块的三个,可以拿到4个点的分剩下的学习大佬的书写
/*
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>using namespace std;vector<string>v;
string str;bool check_title(string s , string &res)
{if(s[0] != '#') return false;if(s[0] == '#') // 标题{int j = 0;while(j < s.size() && s[j] == '#') j ++;int i = 0;while(i < s.size() && (s[i] == '#' || s[i] == ' ')) i ++;string ch = to_string(j);res = "<h" + ch + ">" + s.substr(i) + "</h" + ch + ">";}return true;
}int main()
{while(getline(cin , str)){if(!s.size()) continue;v.push_back(str);}for(auto i : v){string res;// 标题if(check_title(i , res)) cout << res << endl;// 强调else if(check_yes(i , res)) cout << res << endl;// 链接else if(check_link(i , res)) cout << res << endl;}return 0;
}
*/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;vector<string> strs;int work_link(string str, int i)
{string text, link;for (i ++; str[i] != ']'; i ++ ){char c = str[i];if (c == '_'){text += "<em>";i ++ ;while (str[i] != '_') text += str[i ++ ];text += "</em>";}else text += c;}for (i += 2; str[i] != ')'; i ++ )link += str[i];printf("<a href=\"%s\">%s</a>", link.c_str(), text.c_str());return i;
}int work_em(string str, int i)
{printf("<em>");for (i ++; str[i] != '_'; i ++ ){char c = str[i];if (c == '[') i = work_link(str, i);else cout << c;}printf("</em>");return i;
}void work_line(string str)
{int k = 0;while (str[k] == ' ') k ++ ;str = str.substr(k);for (int i = 0; i < str.size(); i ++ ){char c = str[i];if (c == '_') i = work_em(str, i);else if (c == '[') i = work_link(str, i);else cout << c;}
}void work(int a, int b)
{if (strs[a][0] == '#'){int k = 0;while (strs[a][k] == '#') k ++ ;printf("<h%d>", k);work_line(strs[a].substr(k));printf("</h%d>\n", k);}else if (strs[a][0] == '*'){printf("<ul>\n");for (int i = a; i <= b; i ++ ){printf("<li>");work_line(strs[i].substr(1));printf("</li>\n");}printf("</ul>\n");}else{printf("<p>");for (int i = a; i <= b; i ++ ){work_line(strs[i]);if (i != b) cout << endl;}printf("</p>\n");}
}int main()
{string str;while (getline(cin, str)) strs.push_back(str);for (int i = 0; i < strs.size(); i ++ ){if (strs[i].empty()) continue;int j = i + 1;while (j < strs.size() && strs[j].size()) j ++ ;work(i, j - 1);i = j - 1;}return 0;
}第四题:地铁修建
A 市有 n 个交通枢纽,其中 1 号和 n 号非常重要,为了加强运输能力,A 市决定在 1 号到 n 号枢纽间修建一条地铁。
地铁由很多段隧道组成,每段隧道连接两个交通枢纽。
经过勘探,有 m 段隧道作为候选,两个交通枢纽之间最多只有一条候选的隧道,没有隧道两端连接着同一个交通枢纽。
现在有 n 家隧道施工的公司,每段候选的隧道只能由一个公司施工,每家公司施工需要的天数一致。
而每家公司最多只能修建一条候选隧道。所有公司同时开始施工。
作为项目负责人,你获得了候选隧道的信息,现在你可以按自己的想法选择一部分隧道进行施工,请问修建整条地铁最少需要多少天。
输入格式
输入的第一行包含两个整数 n,m,用一个空格分隔,分别表示交通枢纽的数量和候选隧道的数量。
第 2 行到第 m+1 行,每行包含三个整数 a,b,c,表示枢纽 a 和枢纽 b 之间可以修建一条隧道,需要的时间为 c 天。
输出格式
输出一个整数,修建整条地铁线路最少需要的天数。
数据范围
对于 20% 的评测用例,1≤n≤10,1≤m≤20;
对于 40% 的评测用例,1≤n≤100,1≤m≤1000;
对于 60% 的评测用例,1≤n≤1000,1≤m≤10000,1≤c≤1000;
对于 80% 的评测用例,1≤n≤10000,1≤m≤100000;
对于 100% 的评测用例,1≤n≤100000,1≤m≤200000,1≤a,b≤n,1≤c≤1000000。
所有评测用例保证在所有候选隧道都修通时1号枢纽可以通过隧道到达其他所有枢纽。输入样例:
6 6 1 2 4 2 3 4 3 6 7 1 4 2 4 5 5 5 6 6输出样例:
6样例解释
可以修建的线路有两种。
第一种经过的枢纽依次为 1,2,3,6,所需要的时间分别是 4,4,7,则整条地铁线需要 7 天修完;
第二种经过的枢纽依次为 1,4,5,6,所需要的时间分别是 2,5,6,则整条地铁线需要 6 天修完。
第二种方案所用的天数更少。
解题思路:
对于基本前50%的数据可以使用暴力枚举+bfs的方法进行求解,枚举每一个可能的答案进行判断。
但是更快速的方法就是可以使用二分枚举枚举每一个答案,复杂度可以降到log的级别肯定可以通过。
#include<iostream>
#include<queue>
#include<cstring>using namespace std;const int N = 100010 , M = 400010;
int n , m;
int h[M] , e[M] , ne[M] , w[M] , idx;
int dist[N];void add(int a , int b , int c)
{e[idx] = b , w[idx] = c , ne[idx] = h[a] , h[a] = idx ++;
}int bfs(int u)
{memset(dist , 0x3f , sizeof dist);dist[1] = 0;queue<int>q;q.push(1);while(!q.empty()){int t = q.front();q.pop();for(int i = h[t];~i;i = ne[i]){int j = e[i];if(w[i] > u) continue;if(dist[j] > dist[t] + 1){dist[j] = dist[t] + 1;q.push(j);}}}return dist[n];
}int main()
{memset(h , -1 , sizeof h);cin >> n >> m;while(m --){int a , b , c;cin >> a >> b >> c;add(a , b , c) , add(b , a , c);}int r = 1e18 , l = 0;while(l < r){int mid = (l + r) >> 1;if(bfs(mid) <= n) r = mid;else l = mid + 1;}cout << r << endl;return 0;
}第五题:引水入城
最大流、最小割、平面图、分层图最短路、DP
(不会)
#include <iostream>using namespace std;using i64 = long long;const int N = 5010;i64 n, m, A, B, Q, x;
int r[N][N], c[N][N];
i64 d[N];int main() {cin >> n >> m >> A >> B >> Q >> x;for (int i = 1; i <= n - 1; i++)for (int j = 1; j <= m; j++)x = c[i][j] = (A * x + B) % Q;for (int i = 2; i <= n - 1; i++)for (int j = 1; j < m; j++)x = r[i][j] = (A * x + B) % Q;for (int j = 1; j <= m; j++) {for (int i = 1; i < n; i++) d[i] += c[i][j];for (int i = 2; i < n; i++) d[i] = min(d[i], d[i - 1] + r[i][j]);for (int i = n - 2; i; i--) d[i] = min(d[i], d[i + 1] + r[i + 1][j]);}i64 res = 1e18;for (int i = 1; i < n; i++) res = min(res, d[i]);cout << res << '\n';return 0;
}



:申报签署流程与复盘详解)


)












