题目
扫地机器人 - 蓝桥云课 (lanqiao.cn)
https://www.lanqiao.cn/problems/199/learning/?page=1&first_category_id=1&name=%E6%89%AB%E5%9C%B0%E6%9C%BA%E5%99%A8%E4%BA%BA
思路和解题方法
- 首先，通过
cin语句输入了终点位置n和障碍物数量k。- 使用一个数组a来存储k个障碍物的位置。
- 对障碍物位置进行排序，以便后续的二分搜索。
- 然后，定义了一个函数
check，用于检查是否能够在给定的时间内到达终点。该函数采用二分搜索的思想。- 在
check函数中，首先初始化当前位置为起点0。然后遍历每一个障碍物：
- 如果当前位置小于障碍物位置，则需要额外花费时间走过去，时间花费为
(a[i] - pos - 1) * 2。- 若剩余时间不足以到达当前障碍物，则返回false，表示无法在给定时间内到达终点。
- 否则，更新当前位置为走过障碍物后的位置，即
pos = a[i] + t / 2。- 当所有障碍物都走过后，判断当前位置是否小于终点位置n，若小于则返回false，表示无法在给定时间内到达终点；否则返回true，表示可以在给定时间内到达终点。
- 主函数使用二分搜索来找到最短时间。初始化二分搜索的左边界l为0，右边界r为2 * n。
- 在while循环中，计算中间值mid，并调用
check函数判断是否能在mid时间内到达终点。
- 若可以，则更新答案ans为mid，并将右边界r缩小为mid-1，继续搜索更短的时间。
- 若不可以，则将左边界l扩大为mid+1，继续搜索更长的时间。
- 最终输出答案ans，即为最短时间到达终点的结果。
复杂度
时间复杂度:
O(log N * K)
时间复杂度为O(logN * K)，其中N为终点位置，K为障碍物数量。主要时间消耗在二分搜索中。
空间复杂度
O(K)
空间复杂度为O(K)，其中K为障碍物数量，因为需要使用一个数组来存储障碍物的位置。
c++ 代码
#include<iostream>
#include<algorithm>
using namespace std;int n, k, a[100005]; // 定义变量n（终点位置）、k（障碍物数量）、a数组存放k个障碍物的位置
int ans; // 存放最终答案// 检查是否能够在给定的时间内到达终点
bool check(int time)
{int pos = 0; // 当前位置初始化为起点for(int i = 0; i < k; ++i) // 遍历每一个障碍物{int t = time; // t表示剩余时间if(pos < a[i]) // 如果当前位置小于障碍物位置t -= (a[i] - pos - 1) * 2; // 则需要额外花费时间走过去if(t < 0) // 如果剩余时间不足以到达当前障碍物return false; // 返回false，表示无法在给定时间内到达终点pos = a[i] + t / 2; // 更新当前位置为走过障碍物后的位置}if(pos < n) // 如果所有障碍物都走过后，仍未到达终点return false; // 返回false，表示无法在给定时间内到达终点return true; // 否则返回true，表示可以在给定时间内到达终点
}int main()
{cin >> n >> k; // 输入终点位置n和障碍物数量kfor(int i = 0; i < k; i++)cin >> a[i]; // 输入k个障碍物的位置sort(a, a + k); // 对障碍物位置进行排序int l = 0, r = 2 * n; // 初始化二分搜索的左右边界while(l <= r) // 二分搜索{int mid = l + (r - l) / 2; // 取中间值if(check(mid)) // 能够在mid时间内到达终点ans = mid, r = mid - 1; // 更新答案并缩小右边界elsel = mid + 1; // 否则扩大左边界}cout << ans << endl; // 输出答案return 0;
}
未优化的代码 暴力 time从0~2*n
for(int i = 0;i<=2*n;i++){if(check(i)){ans = i;break;}}时间对比
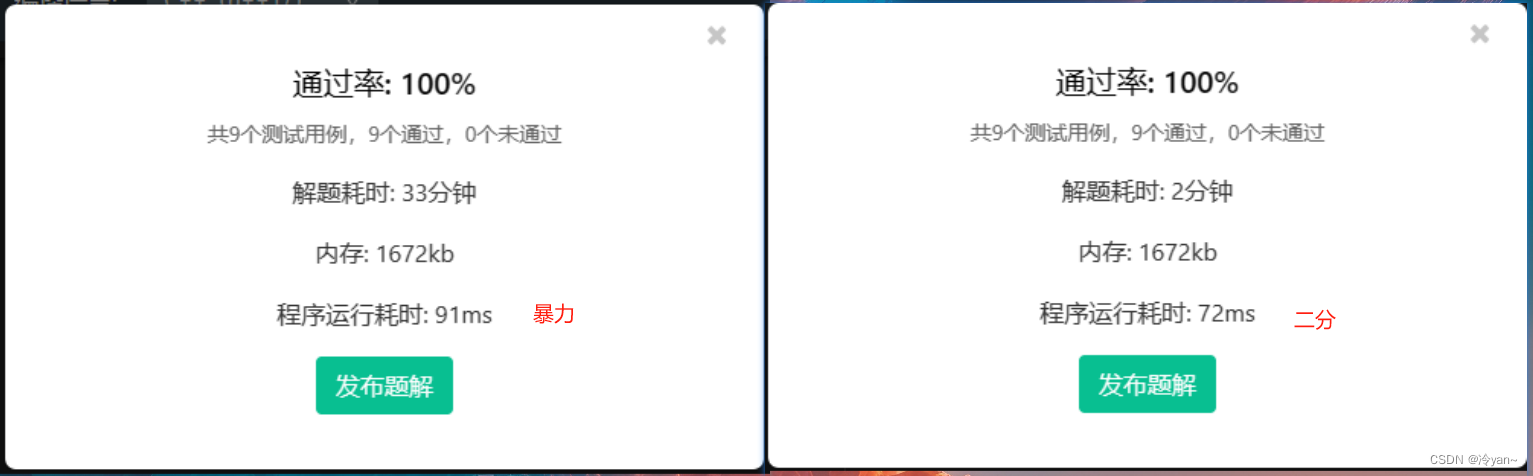
我的文档里面也有许多二分（双指针）题目，可供大家参考作答。
双指针_冷yan~的博客-CSDN博客https://blog.csdn.net/jgk666666/category_12470278.html
觉得有用的话可以点点赞，支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
