前言:该系列实验均使用matlab完成,实验课程为《数字信号处理》
文章目录
- 一.题目
- 二.实验目的
- 三.实验仪器
- 四.实验原理
- 实验所用的matlab函数解析
- 离散时间信号实验原理:
- 五.实验步骤
- 六.实验代码及实验结果
- 完整代码
- 1.线性卷积代码
- 2.循环卷积运算代码
- 七.实验结论及分析讨论
一.题目
已知序列x[k]={1,2,3.4},y[k]={-1,1,2,3},试计算序列x[k]与yk]的线性卷积,并验证循环卷积与线性卷积的结果相同时的条件。
二.实验目的
1.掌握卷积的原理;
三.实验仪器
计算机,MATLAB软件
四.实验原理
实验所用的matlab函数解析
- sound: 播放声音
(1)sound(Y,Fs): 将向量Y(具有采样频率FS)中的信号发送到支持声音的平台上的扬声器。
(2)sound(Y):以默认采样率播放声音
(3)sound(Y,Fs,BITS):使用样本播放声音
2.num2str: 将数值转换为字符串
3.disp: 用来展示变量的内容,可以是字符串,矩阵,结构体。 - conv: 卷积函数,用于两个信号的卷积
5.subplot:将多图画到一个平面上的工具。
离散时间信号实验原理:
1.线性卷积
线性时不变系统输入、输出间的关系为:当系统输入序列为x(n) ,系统的单位脉冲响应为h(n),输出序列为y(n),则系统输出为:
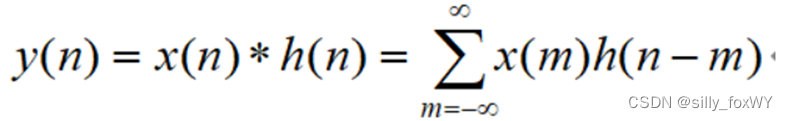
上式称为线性卷积
2.循环卷积
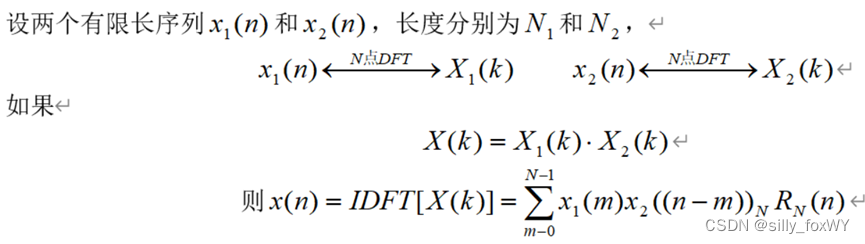
上式称为x1(n)和x2(n)的循环卷积
3.循环卷积与线性卷积的关系

五.实验步骤
- 已知序列x[k]={1,2,3,4},y[k]={-1,1,2,3},试计算序列x[k]与y[k]的线性卷积,并验证循环卷积与线性卷积的结果相同时的条件。
六.实验代码及实验结果
完整代码
1.线性卷积代码
%线性卷积的运算
x = [1,2,3,4] %创建序列x[k]={1,2,3,4},k从0开始
y = [-1,1,2,3] %创建序列y[k]={-1,1,2,3},k从0开始
h = conv(x,y) %序列x[k]与y[k]卷积,结果记录为h
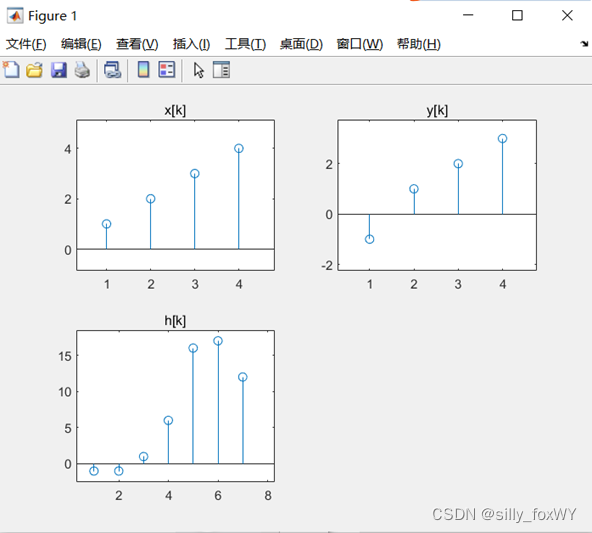
subplot(2,2,1);stem(k,x);title('x[k]'); %绘制序列x[k]图像
subplot(2,2,2);stem(k,y);title('y[k]'); %绘制序列y[k]图像
subplot(2,2,3);stem(k,h);title('h[k]'); %绘制线性卷积结果图像
线性卷积运行结果:
2.循环卷积运算代码
%循环卷积的运算
%cconv 函数用于计算两个有限长序列的循环卷积
%x:长度为N的有限长序列,N = 4
%y:长度为M的有限长序列,M = 4
%L:循环卷积的长度
%l:线性卷积输出序列长度l = N+M-1=7
%h:x与y的循环卷积结果,L>=max(N,M)
x = [1,2,3,4] %创建序列x[k]={1,2,3,4},k从0开始
y = [-1,1,2,3] %创建序列y[k]={-1,1,2,3},k从0开始
L = 9 %设置循环卷积的长度
h = cconv(x,y,L) %计算循环卷积
循环卷积运行结果:
- 当L<N+M-1时(程序代码中修改L=6)

- 当L=N+M-1时(程序代码中修改L=7)

- 当L>N+M-1时(程序代码中修改L=9)

综上验证可得:
(1) 当L<N+M-1时,循环卷积是线性卷积长度为L的混叠;
(2) 当L=N+M-1时,循环卷积=线性卷积;
(3) 当L>N+M-1时,循环卷积是线性卷积末尾补L-(N+M-1)个零;
七.实验结论及分析讨论
1.在离散时间信号的分析实验中,循环卷积与线性卷积结果相同的条件是:L=N+M-1。
循环卷积与线性卷积的关系为:
(1) 当L<N+M-1时,循环卷积是线性卷积长度为L的混叠;
(2) 当L=N+M-1时,循环卷积=线性卷积;
(3) 当L>N+M-1时,循环卷积是线性卷积末尾补L-(N+M-1)个零;


解决windows11无法使用1500000波特率的问题)
)







)



)





)