信号类型（通信）——最小频移键控（MSK）

系列文章目录

《信号类型（通信）——仿真》

《信号类型（通信）——QAM调制信号》

《信号类型（通信）——QPSK、OQPSK、IJF_OQPSK调制信号》

前言

本文为MSK调制信号的学习笔记，介绍了MSK调制起源，即MSK是一种特殊的FSK调制。并根据MSK信号特征由FSK信号模型推导了MSK的信号模型；并基于MSK信号模型介绍了MSK信号调制与解调原理；最后结合仿真加深对MSK信号调制与解调的理解。此外补充了MSK信号的频谱表达式，公式的具体推导没有研究，文后有参考文献，感兴趣的可以自行推导，也欢迎在评论区给出相应的推导过程。（文末有彩蛋）

一、MSK信号特点

最小频移键控（MSK）调制方式是频移键控（FSK）调制方式的特例。相比于FSK调制，MSK调制满足两个条件：正交条件下最小频率间隔（最大频移为比特速率的1/4）；信号相位连续。满足上述条件的MSK信号能量99.5%被限制在数据传输速率的1.5倍的带宽内。此外MSK属于恒包络数字调制技术，系统可以使用廉价高效的非线性器件。下面基于最小频移以及相位连续两个条件简单推导MSK信号模型。

1.1、最小频移

针对01码元对应波形的正交条件，假设FSK码元波形为：

$e_{n}(t)=\left\{\begin{matrix} A\cos(2\pi f_1 t+\varphi_1),a_n=1\\ A\cos(2\pi f_0 t+\varphi_0),a_n=0 \end{matrix}\right. \; \: \: \: \: \: \: \: \: \: \: \: \: (1)$

考虑FSK调制码波形的正交性，有：

$\int_{0}^{T_B}\cos(2\pi f_1 t+\varphi_1 )\cos(2\pi f_0 t+\varphi_0)dt=0 \; \: \: \: \: \: \: \: \: \: \: \: \: (2)$

分别根据积化和差公式、定积分公式以及 $2\pi f_1+2\pi f_0\gg 1$ 的假设条件，可以得到：

$\cos(\varphi_1-\varphi_0)\sin((\omega_1-\omega_0)T_B) +\sin(\varphi_1-\varphi_0)[\cos((\omega_1-\omega_0)T_B) -1]=0$ (3)

为了使上式在任意 $\varphi_1, \varphi_0$ 的下都成立，则需要满足：

$f_1-f_0=\frac{m}{T_B} \; \: \: \: \: \: \: \: \: \: \: \: \:(4)$

此时只能采用非相干检波法接收。针对相干接收，初始相位确定，当 $\sin(\varphi_1-\varphi_0)=0$ ，则仅需要满足:

$f_1-f_0=\frac{m}{2T_B} \; \: \: \: \: \: \: \: \: \: \: \: \:(5)$

1.2、相位连续

在最小频差为 $\frac{1}{2T_B}$ 下，可令MSK信号模型为：

$e_{n}(t)=\cos(2\pi f_c t+\frac{a_n\pi}{2T_B}t+\varphi_n),nT_B\leq t\leq (n+1)T_B \; \: \: \: \: \: \: \: \: \: \: \: \:(6)$

为了保证码元波形的正交性，此时载频 $f_c$ 需要满足：

$f_c=\frac{n}{4T_B} \; \: \: \: \: \: \: \: \: \: \: \: \:(7)$

考虑相位 $2\pi f_c t$ 是连续，MSK信号中 $\frac{a_n\pi}{2T_B}t$ 相位是存在跳变，需要通过调整 $\varphi_n$ 使得MSK信号相位连续，即需要满足：

$\frac{a_{n-1}\pi}{2T_B}nT_B+\varphi_{n-1}=\frac{a_n\pi}{2T_B}nT_B+\varphi_n \; \: \: \: \: \: \: \: \: \: \: \: \:(8)$

由此可得：

$\varphi_n=\varphi_{n-1}+\frac{n\pi}{2}\left ( a_{n-1}-a_n \right )=\left\{\begin{matrix} \varphi_{n-1},a_{n-1}=a_n\\ \varphi_{n-1}\pm n\pi,a_{n-1}\neq a_n \end{matrix}\right. \; \: \: \: \: \: \: \: \: \: \: \: \:(9)$

为了满足 $\sin(\varphi_1-\varphi_0)=0$ ，则 $mod(a_{n-1}-a_n,2)=0$ ，因此需要将原始01码通过双极性转换，得到+1，-1码。将MSK信号进行IQ正交分解得：

$e_{n}(t)=p_n \cos\frac{\pi}{2T_B}t\cos\omega_c t-q_n \sin\frac{a_n\pi}{2T_B}t\sin\omega_c t,nT_B\leq t\leq (n+1)T_B$ (10)

其中

$\begin{matrix} p_n=\cos\left ( \varphi_n \right )=\pm 1\\ q_n=a_n\cos\left ( \varphi_n \right )=a_np_n=\pm 1 \end{matrix}\: \: \: \: \: \: \: \: \: \: \: (11)$

二、MSK调制与解调

2.1、调制原理

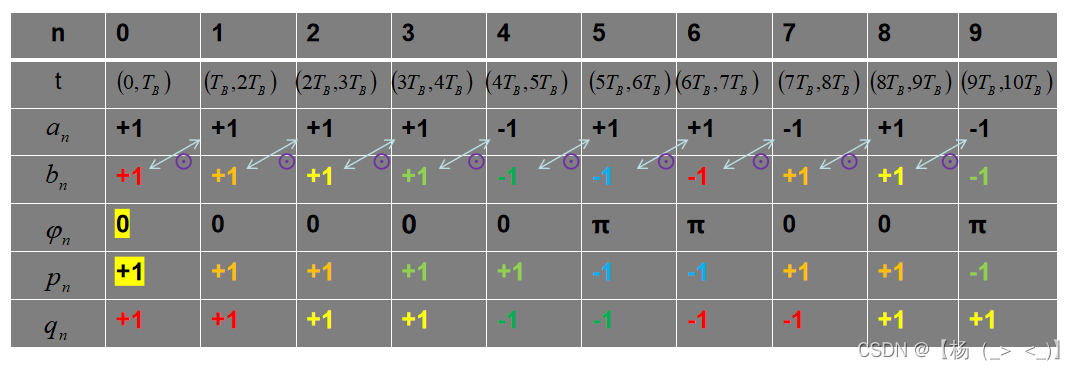
MSK信号可以按照公式（10）生成，我们可以根据公式（9）计算 $\varphi_n$ ，再由公式（11）计算得到 $p_n,q_n$ ，但是这种信号生成方式在实际电路实现时并不方便，为此引入上图表所示的 $p_n,q_n$ 的生成方案，首先基于差分编码生成码序列：

$b_n=b_{n-1}\bigodot a_n\: \: \: \: \: \: \: \: \: \: \: (12)$

其中 $\odot$ 表示同或， $b_1= a_1$ 。

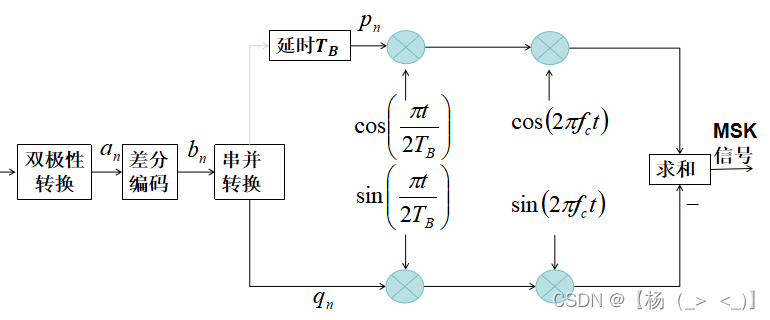上图表示MSK信号生成的流程图，首先01比特流经过双极性转换变成双极性码 $\pm 1$ ，在经过差分编码以及串并转换得到 $p_n,q_n$ ，再分别经过半个波特的频率调制以及载频调制混合得到最终发射的MSK信号。

2.2、解调原理

对公式（10）所示MSK信号进行载波提取得到：

$\begin{matrix} I(t)=p_n \cos\frac{\pi}{2T_B}t\\ Q(t)=q_n \sin\frac{\pi}{2T_B}t \end{matrix}\: \: \: \: \: \: \: \: \: \: \: (13)$

则在I路采样判决点上对应的I值为：

$\begin{matrix} I(2nT_B+2T_B)=-p_{2n+1} \cos n\pi\\ I(2nT_B+2T_B)=-p_{2n+2} \cos n\pi\end{matrix}\: \: \: \: \: \: \: \: \: \: \: (14)$

则在Q路采样判决点上对应的Q值为：

$\begin{matrix} Q(2nT_B+T_B)=q_{2n} \cos n\pi=a_{2n}p_{2n} \cos n\pi\\ Q(2nT_B+T_B)=q_{2n+1} \cos n\pi=a_{2n+1} p_{2n+1}\cos n\pi\end{matrix}\: \: \: \: \: \: \: \: \: \: \: (15)$

由公式（14）（15）可得：

$\begin{matrix} Q(2nT_B+3T_B)=a_{2n+2}I(2nT_B+2T_B)\\ Q(2nT_B+T_B)=-a_{2n+1} I(2nT_B+2T_B)\end{matrix}\: \: \: \: \: \: \: \: \: \: \: (16)$

我们可以对上述采样值大于0的判为+1，小于0判为-1，然后基于公式（16）还原出 $a_n$ ，为了提高信噪比，我们可以在采样点附近左右对称的区域 $T_B$ 内求积分得到信噪比更好的判决统计量。最终解调原理图下：

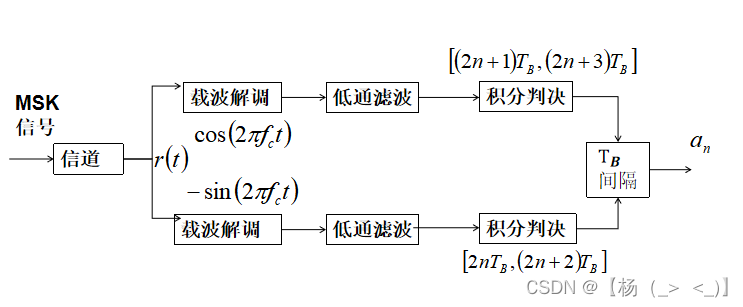
此外由公式（13）构成的复信号 $I(t)+j Q(t)$ 可以得到相位历程：

$\theta_{n}(t)=\frac{a_n\pi}{2T_B}t+\varphi_n \; \: \: \: \: \: \: \: \: \: \: \: \:(17)$

由此相位历程也可以解调出 $a_n$ 。

三、MSK信号频谱

对公式（10）进行积化和差得：

$e_{n}(t)=c_{n}\cos(\omega_c-\frac{\pi}{2T_B}) t+d_{n}{2}\cos(\omega_c+\frac{\pi}{2T_B}) t\; \: \: \: \: \: \: \: \: \: \: \: \:(18)$

其中 $c_{n}=\frac{p_n-q_n}{2},d_{n}=\frac{p_n+q_n}{2}$ ，根据 $p_{n},q_{n}$ 错位延时的特点， $c_n,d_n\in \left ( -1,0,1 \right )$ 的变化周期为 $T_B$ 。考虑随机生成的码序列，MSK信号功率谱密度为：

$P(f)=\frac{8P_cT_B\left ( 1+\cos\left (4\pi (f-f_c) T_B \right ) \right )}{\pi^2\left ( 1-16T_B^2 (f-f_c)^2 \right )^2}\; \: \: \: \: \: \: \: \: \: \: \: \:(19)$

其中 $P_c$ 表示被调制波形功率，从公式（18）可以看出MSK信号功率谱密度随偏移载频量的四次方成反比衰减，带外能量泄露很少。

四、仿真

参数设置，符号速率60kHz，采样率12 Mz，载频 1.5MHz，码序列随机生成。

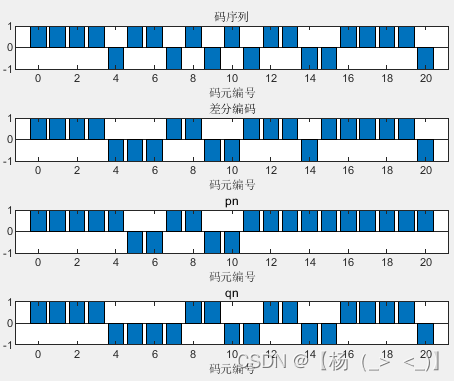
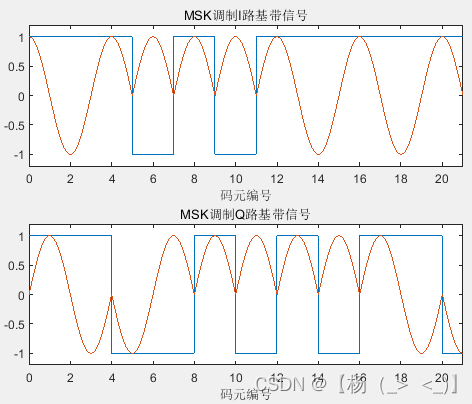
IQ两路码信号生成 MSK调制的基带IQ信号

左上图分别为双极化后的码，差分编码输出结果，MSK调制得到IQ两路码表示 $p_n,q_n$ 。右图是调制半个波特频率后的基带信号，可以看出 $p_n$ 只在 $n$ 为奇数的时候发生变化， $q_n$ 只在 $n$ 为偶数时发生变化。

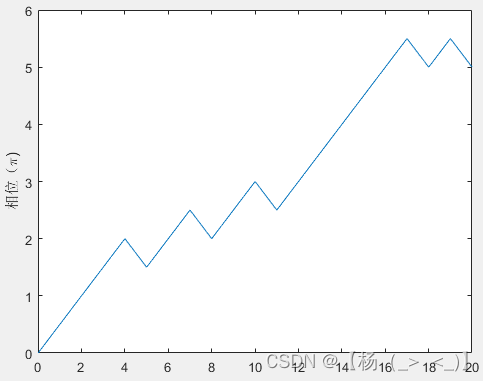
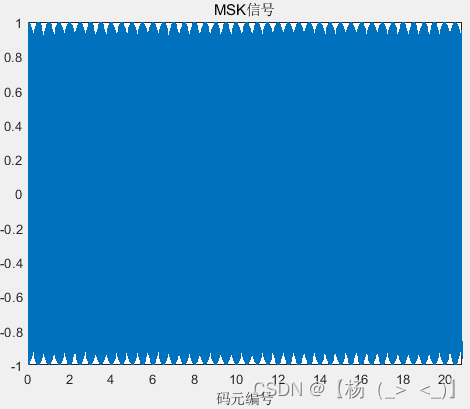
MSK基带信号的相位历程 MSK信号

左上图为MSK基带信号的相位历程，可以看出信号只有两种频率成分，且相位连续，右图是对应的MSK已调信号，信号基本横包络。

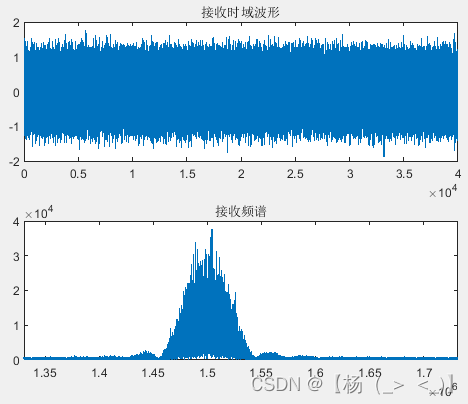
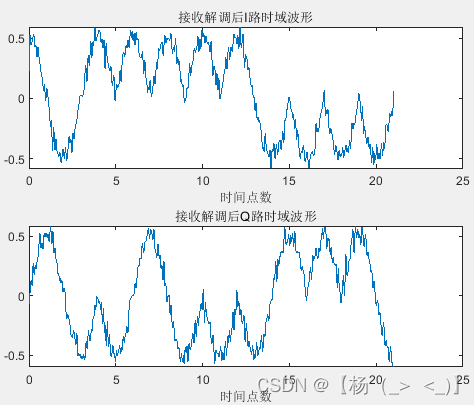
加噪的MSK信号载波提取后的信号

上图为只考虑接收机热噪声影响下的接收信号以及载波提取后的信号，可以看出，噪声对信号产生了干扰，下图为对应的IQ两路信号的眼图，可以看出IQ两路信号存在码长大小的延时。

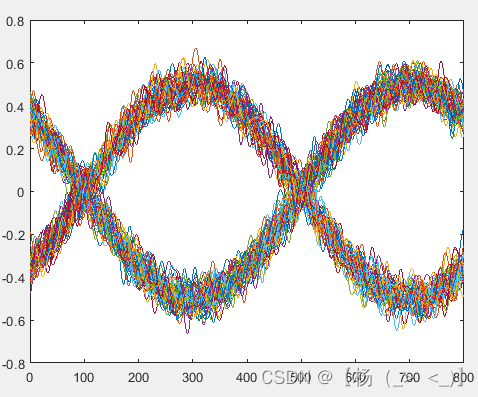
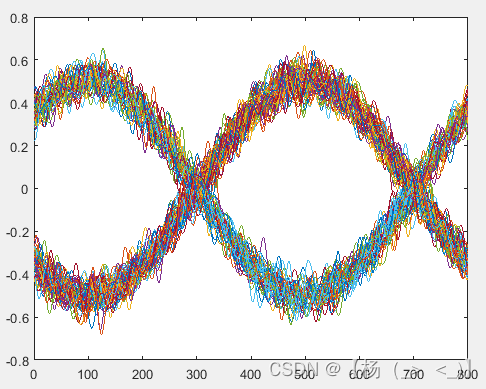
积分前I路眼图积分前Q路眼图

对接收的IQ信号进行积分得到下图所示的眼图，可以看出眼图的展宽降低，对应的信噪比得到显著提升。

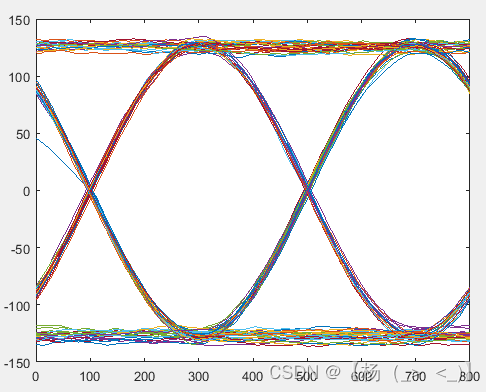
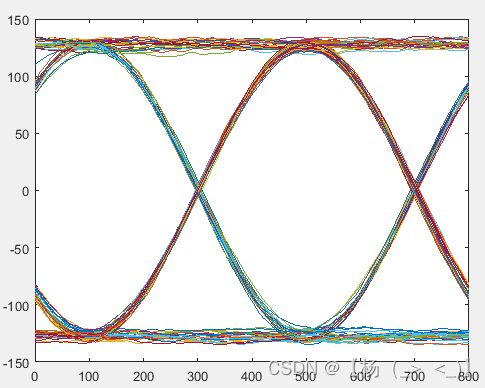
积分后I路眼图积分后Q路眼图

最后分析了不同信号长度（1、2、4、10、100、1000符号长度）下的信号功率频谱与理论值的差异，可以看出随着信号长度增加，信号功率谱形状趋于公式（18）所示的功率谱形状。

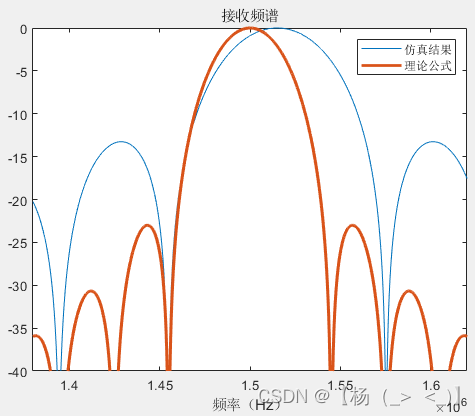
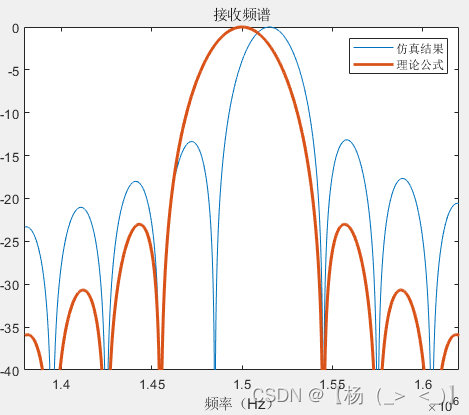
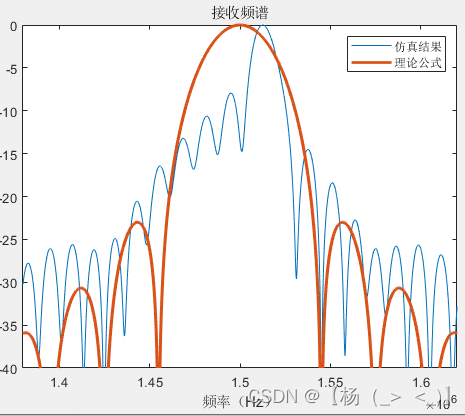
1 2 4

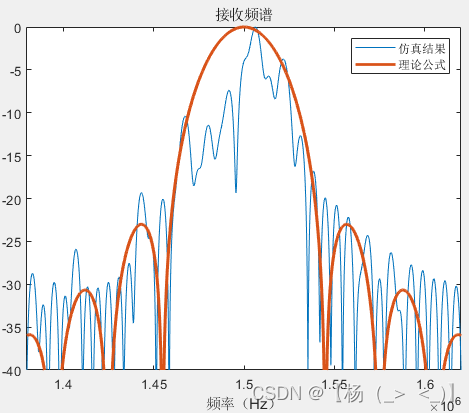
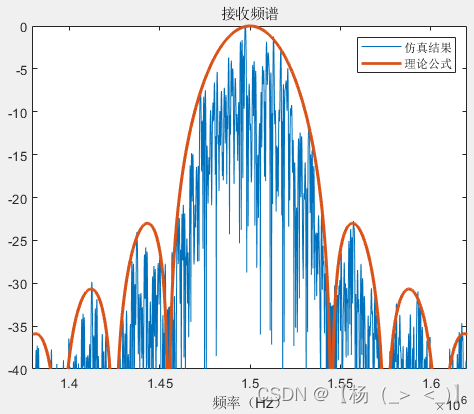
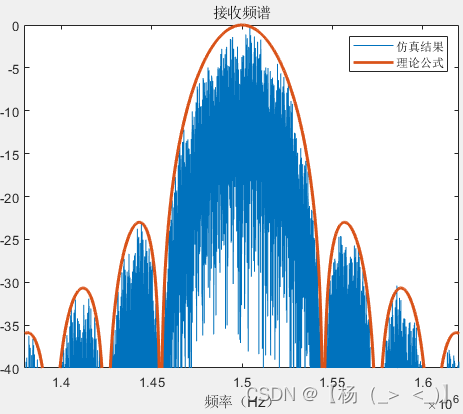
10 100 1000

参考文献

1、樊昌信曹丽娜《通信原理》第7版

2、S. Gronemeyer and A. McBride, "MSK and Offset QPSK Modulation," in IEEE Transactions on Communications, vol. 24, no. 8, pp. 809-820, August 1976, doi: 10.1109/TCOM.1976.1093392.

总结

本文根据自己的理解从理论和仿真的角度介绍了MSK调制与解调原理，其中关于IQ路的延时处理可能和其他资料有所不同。有更好的内容欢迎在评论区放置链接，另外有问题也欢迎评论区留言。转载请附链接【杨（_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主

二周年纪念

目前《SAR学习笔记》观看量最多，有1.4w，阅读量过万的文章有两篇，另一篇《SAR学习笔记-SAR成像算法系列（一）》，阅读量过5千的文章有8篇，涉及：SAR，呼吸信号处理，Gold序列。整个创作，获得285次点赞，内容获得250次评论，获得1,843次收藏，代码片获得732次分享，资源总下载次数300多次。总阅读量14w。对于这样一个结果，博主还是很满意的。当然博主也欢迎各位看官有好的资源可以在评论区放置链接。根据目前情况，后期博主将对SAR领域中的干涉SAR、极化SAR、逆SAR内容进行补充。近期主要更新与信号类型有关的文章。当然，如果有什么信号处理的理论技术需要博主补充的可以评论区留言。