假设你想创建一个甜蜜的弹跳立方体,如下所示:

一个弹跳的立方体
你可以使用 3D 框架,例如 OpenGL 或 Metal。 这涉及编写一个或多个顶点着色器来变换 3D 对象,以及编写一个或多个片段着色器来在屏幕上绘制这些变换后的对象。
然后,该框架采用这些着色器和您的 3D 数据,执行一些魔法,并以绚丽的 32 位颜色绘制所有内容。
但 OpenGL 和 Metal 在幕后到底有什么魔力呢?
在线工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器
回到过去—早在我们拥有硬件加速 3D 显卡之前,更不用说可编程 GPU 了—如果你想绘制 3D 场景,你必须自己完成所有工作, 在只有 7 MHz 处理器的计算机上,用汇编语言。
我的书架上摆满了有关 3D 图形的书籍,但这些书籍已经过时了,因为现在你可以简单地使用 OpenGL 或 Metal。 我很高兴我们能做到! 然而,即使你利用这些现代 GPU 和 3D API,了解在屏幕上绘制 3D 对象所涉及的步骤仍然很有用。
在这篇文章中,我将解释如何使用简单的动画和光照,但不使用着色器来绘制 3D 弹跳立方体。 它说明了当你使用 OpenGL 或 Metal 时会发生什么,我将指出现代顶点和片段着色器在这个故事中的应用。
我们根本不会使用任何 3D API—这只是最基本的。 我们可以使用的唯一渲染基元是 setPixel() 函数,用于将单个像素写入 800×600 位图:
func setPixel(x: Int, y: Int, r: Float, g: Float, b: Float, a: Float)这会将位图坐标 (x, y) 处的像素更改为颜色 (r, g, b, a)。 为了进行 3D 绘制,我们需要做的所有其他事情都建立在这个非常基本的 setPixel() 函数之上,下面将详细解释。
注意:我们不会使用任何花哨的数学,只会使用基本算术和一点三角函数。 数学不涉及矩阵,因此你可以准确地看到何时发生什么以及为什么发生。 即使你在学校数学没及格,你也应该能够跟上!
读完这篇文章后,你将能够从头开始编写自己的基本 3D 渲染器,并更好地了解 OpenGL 和 Metal 管道的工作原理。
1、演示应用程序
如果你想先查看完成的应用程序,可以在 GitHub 上找到完整的源代码。 这是一个 macOS 应用程序,用 Swift 3 编写。语言并不重要,你可以轻松地将其移植到任何其他语言。
只需在 Xcode 8 中打开项目并运行即可。 该演示展示了一个上下弹跳并绕垂直轴旋转的彩色立方体:
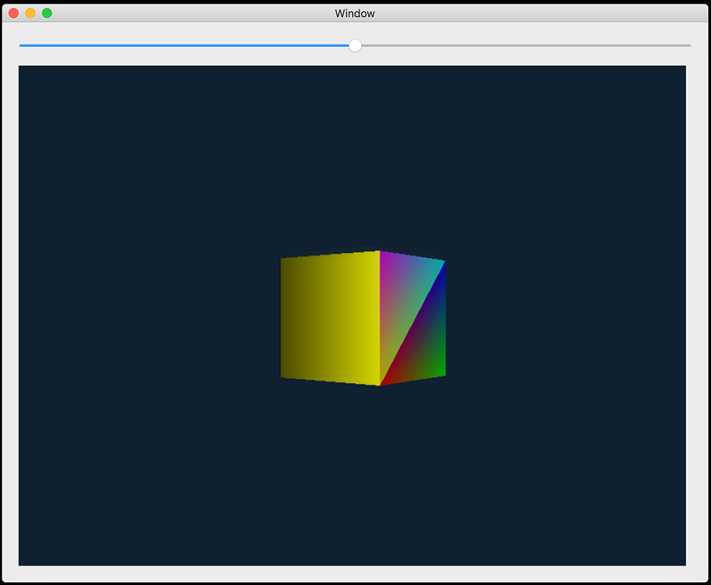
顶部的滑块可向左或向右移动相机,让你从不同的有利位置观察立方体。
该应用程序并不是特别漂亮,但它确实演示了 3D 渲染中涉及的许多概念。
注意:取决于你的Mac 的速度,演示应用程序可能运行速度相当慢。 毕竟,这篇博文并不是如何制作快速 3D 图形的示例—这才是 GPU 的用途。 我在这里的目标只是展示基本想法是如何工作的,因此我们为了清晰度和易于理解而牺牲速度。
所有重要的代码都在 Render.swift 文件中。 代码里有很多解释,因此你可以只阅读源代码而不是这篇博文。 😉
简而言之,演示应用程序中发生的事情是这样的:函数 render() 获取一些 3D 模型数据(立方体),对其进行转换和投影,然后通过一遍又一遍地调用 setPixel() 来绘制它 — 这也是它这么慢的原因。
render() 中发生的情况大致相当于你告诉 OpenGL 或 Metal 在屏幕上绘制 3D 内容时 GPU 上发生的情况。 但我们不使用着色器,而是手动完成这一切。
让我们看一下实现这一目标所需的所有部分。
2、3D模型
首先我们定义模型。 这就是我们要绘制的 3D 对象。 该模型由三角形组成,因为三角形很容易绘制。 这些三角形也称为模型的几何形状。
立方体的几何形状如下所示:
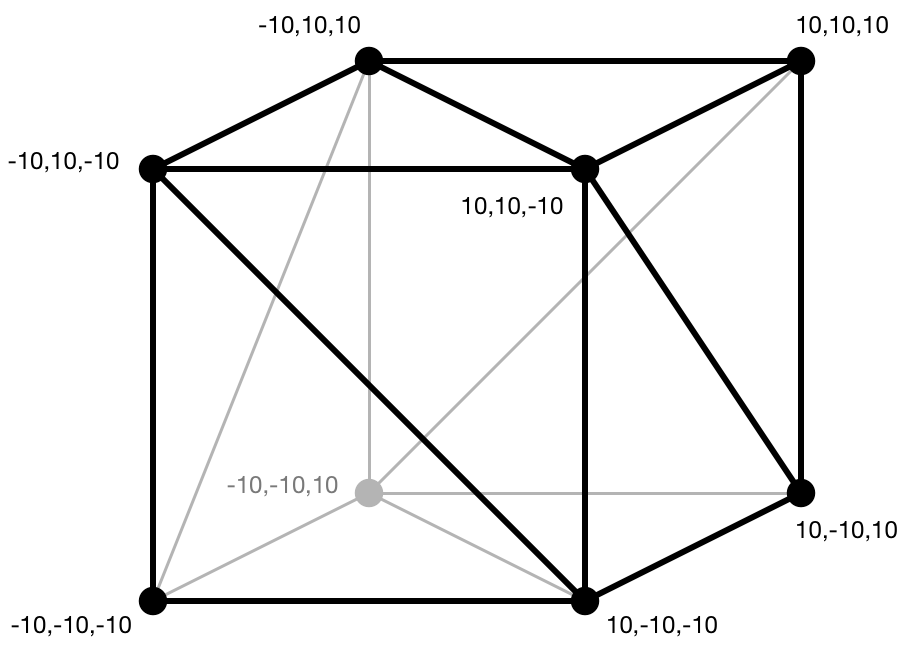
正如你所看到的,该立方体的大小从 -10 单位到 +10 单位。 单位可以是任何你想要的,比如说厘米。
我们使用的坐标系如下所示:
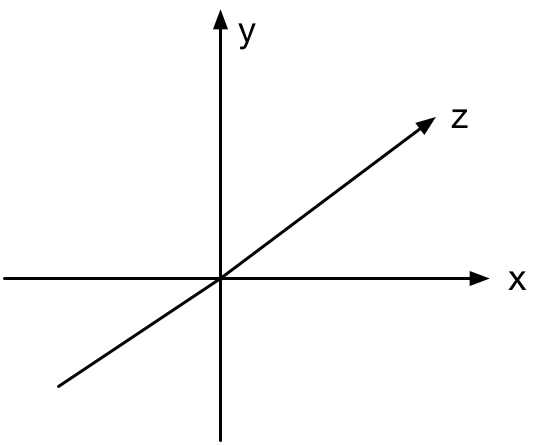
左手坐标系
x 坐标向右为正,y 为向上正,z 为进入屏幕正。 这就是所谓的左手坐标系。
注意:轴的选择有些随意。 要获得右手坐标系(其中 z 从屏幕中出来为正值),只需将所有地方的 z 更改为 -z 即可。 左手还是右手的选择决定了某些事情(例如旋转)是按顺时针还是逆时针顺序发生。
每个三角形由 3 个顶点组成。 顶点描述 3D 空间中的 (x, y, z) 位置,还描述该顶点处三角形的颜色以及用于照明计算的法线向量。 你还可以添加额外的信息,例如纹理映射坐标,以及想要与顶点关联的任何其他数据。
struct Vertex {var x: Float = 0 // coordinate in 3D spacevar y: Float = 0var z: Float = 0var r: Float = 0 // colorvar g: Float = 0var b: Float = 0var a: Float = 1var nx: Float = 0 // normal vector (using for lighting)var ny: Float = 0var nz: Float = 0
}struct Triangle {var vertices = [Vertex](repeating: Vertex(), count: 3)
}注意:在真实的应用程序中,你可能会使用向量 3 和向量 4 结构而不是单独的属性,但我想向你展示数学,而不需要任何向量或矩阵对象。
为了实现立方体的 3D 模型,我们只需要提供这些三角形的列表。 你通常会在 Blender 等工具中设计模型并从 .obj 文件加载它,但因为这是一个简单的演示,我们手动定义几何形状:
let model: [Triangle] = {var triangles = [Triangle]()// The first trianglevar triangle = Triangle()triangle.vertices[0] = Vertex(x: -10, y: -10, z: 10, // positionr: 0, g: 0, b: 1, a: 1, // color nx: 0, ny: 0, nz: 1) // normaltriangle.vertices[1] = Vertex(x: -10, y: 10, z: 10, r: 0, g: 0, b: 1, a: 1,nx: 0, ny: 0, nz: 1)triangle.vertices[2] = Vertex(x: 10, y: -10, z: 10, r: 0, g: 0, b: 1, a: 1,nx: 0, ny: 0, nz: 1)triangles.append(triangle)// The second triangletriangle = Triangle()triangle.vertices[0] = Vertex(x: -10, y: 10, z: 10, r: 0, g: 0, b: 1, a: 1,nx: 0, ny: 0, nz: 1)triangle.vertices[1] = // . . . and so on . . . return triangles
}()该模型中有 12 个三角形,因此总共有 36 个顶点。 每个顶点都有自己的位置 (x, y, z)、颜色 (r, g, b, a) 和法线向量 (nx, ny, nz)。
法向量的长度应为 1,且指向远离三角形的方向。 这决定了三角形面向的方向,我们需要计算任何灯光的影响。
注意:你可能已经注意到,在上面的立方体几何图形中,只有 8 个顶点,而不是 36 个。 我们只需 8 个顶点就足够了,但不同的三角形也会共享这些顶点的颜色和法向量,而不仅仅是它们的位置。 当你想要在多个三角形之间共享相同的顶点数据时,除了顶点数据之外,OpenGL 和 Metal 还允许你创建所谓的“索引缓冲区”,但我们在这里不这样做。
请注意,某些 x、y、z 坐标位于 -10,某些位于 +10。 这样做是为了使立方体的中心位于原点 (0, 0, 0)。 这称为模型的本地原点 —我们需要这个本地原点,以便围绕其中心旋转对象。
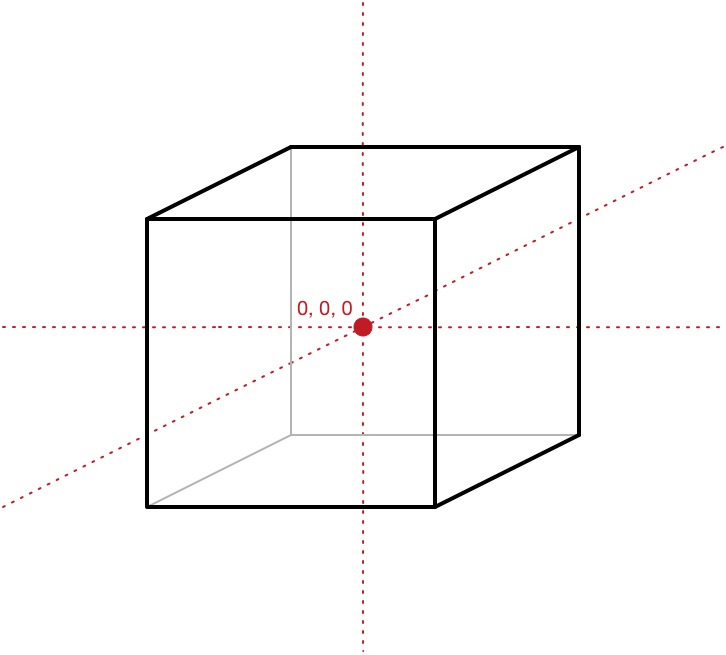
即使我们希望立方体位于 3D 世界的其他位置而不是原点,我们仍然设计模型,使其中心位于 (0, 0, 0)。 然后,我们将把立方体移动到它在世界中的最终位置。 这就是下一节中发生的事情。
3、3D模型在世界中的位置
立方体不仅具有决定其形状的顶点和三角形,而且还具有 3D 世界中的位置、比例以及由三个旋转角度(也称为俯仰/pitch、滚动/roll和偏航/yaw)给出的方向。 我们为这些属性定义变量:
var modelX: Float = 0
var modelY: Float = 0
var modelZ: Float = 0var modelScaleX: Float = 1
var modelScaleY: Float = 1
var modelScaleZ: Float = 1var modelRotateX: Float = 0
var modelRotateY: Float = 0
var modelRotateZ: Float = 0最初,我们将模型放置在世界中心的坐标 (0, 0, 0) 处,在每个方向上为其指定比例 1(或 100%),并将所有旋转角度设置为零。
ViewController.swift 中有一些执行动画的代码。 它有一个每隔几毫秒触发一次的计时器。 在timer方法中,我们对上述变量进行更改,这使得立方体在3D世界中移动,然后我们调用 render()来重绘整个3D场景来显示这些变化。
例如,为了使立方体弹起,我们更改 modelY 变量,以便立方体上下移动。 当立方体撞击地板时,通过更改 modelScaleX/Y/Z,它会稍微“变平”。 立方体看起来在旋转,因为在每个动画步骤中我们都会增加 modelRotateY。
还记得该模型有所谓的“本地”原点吗? 这会告诉你模型的中心在哪里。 世界中心和模型中心之间存在概念上的差异,尽管两者都有坐标 (0, 0, 0)。 模型在世界范围内的任何移动都与本地原点相关。
对于我们当前定义的立方体,其本地原点位于立方体的正中心。 但是,如果你从 .obj 文件加载模型,则本地原点可能并不完全位于你想要的位置。 我们可以通过声明模型的本地原点相对于其顶点位置的位置来解决此问题:
var modelOriginX: Float = 10
var modelOriginY: Float = 0
var modelOriginZ: Float = 10请注意,这里我们没有使用 (0, 0, 0),而是使用 (10, 0, 10),它是立方体的角之一。 旋转围绕这个本地原点进行,只是为了好玩,演示应用程序将围绕一个角而不是中心旋转。
如果你正在运行演示应用程序,请随意使用这些变量和动画代码中的任何一个,看看会发生什么。 很有趣!
4、相机
到目前为止,我们已经定义了一个 3D 对象并在 3D 世界中给了它一个位置。 立方体当前位于世界的中心,我们可以通过更改模型的变量来移动它 — 这就是我们让它上下弹跳的方式。
但作为观察者,你坐在世界的哪个位置呢? 目前,你还坐在原点,即正好位于立方体的中间。 如果我们现在渲染 3D 场景,你会从内到外看到立方体。
我们可以引入一个相机对象,它在3D世界中也有一个位置。 该对象没有任何几何形状,但它只是表示观察者在世界中的位置以及正在看的位置。
var cameraX: Float = 0
var cameraY: Float = 20
var cameraZ: Float = -20在演示应用程序中,我将相机向上移动了 20 个单位,因此你可以稍微向下看场景:可以看到立方体的顶部,但看不到其底部。
相机还沿着 Z 轴向后拉 -20 个单位,使得立方体看起来好像从观察者移开并进入屏幕。 换句话说,我们将从“安全”距离观察立方体。
当你拖动应用程序中的滑块时,会更改cameraX。
注意:在真实的应用程序中,你还可以为相机指定一个方向(使用“查看”向量或使用旋转角度),但在此应用程序中,你始终沿着正 z 轴查看。
5、灯光
当我们定义立方体的 3D 几何形状时,我们为每个顶点指定了一种颜色。 我们可以简单地使用三角形顶点的颜色来绘制三角形,但这有点乏味。 为了使 3D 场景看起来更有趣,我们希望拥有逼真的灯光效果。
以下选项控制场景的照明。 首先,有环境光,这是始终存在的“背景”光:
var ambientR: Float = 1
var ambientG: Float = 1
var ambientB: Float = 1
var ambientIntensity: Float = 0.2我们在这里定义的环境光是纯白色的,但只有 20% 的强度。 这意味着当我们应用此光时,我们将顶点颜色乘以 (0.2, 0.2, 0.2),使它们变得更暗 — 没关系,因为我们还将应用定向照明以使它们再次变得更亮。
你可以使用这些环境设置来给整个场景带来某种感觉。 例如,如果设置 ambientB = 0,那么所有顶点将仅保留其红色+绿色分量,并且所有蓝光将被滤除。
如果将 ambientIntensity设置为0.0,那么在没有任何其他光源的情况下,立方体将是全黑的。 如果设置为 1.0,环境光会淹没任何其他光源。
我们还定义了漫射光源。 与环境光一样,它有颜色和强度,但也有方向:
var diffuseR: Float = 1
var diffuseG: Float = 1
var diffuseB: Float = 1
var diffuseIntensity: Float = 0.8var diffuseX: Float = 0 // direction of the diffuse light
var diffuseY: Float = 0 // (this vector should have length 1)
var diffuseZ: Float = 1对于我们的演示应用程序,漫射光源指向 z 轴正方向,这意味着有一个光源与相机观察的方向相同。 立方体的一侧与相机(以及光源)对齐得越多,它就会显得越亮。
在左下图中,立方体的绿色面面向定向光,因此它显示为亮绿色。 但当立方体旋转远离光线时,绿色的一面变得更暗(蓝色的一面变得更亮):

立方体上方没有光源照射,因此顶部的红色三角形看起来很暗,因为它们仅被环境光照亮。
6、渲染管线
好的,到目前为止我们刚刚定义了 3D 场景将使用的数据结构和变量。 现在是时候展示如何在屏幕上实际渲染这个 3D 世界了。
每个动画帧都会调用 render() 函数。 该函数获取模型的顶点数据、其状态(modelX、modelRotateY 等)和相机的位置,并生成 3D 场景的 2D 再现。
在真实游戏中,`render()` 理想情况下每秒调用 60 次(或更多)。 使用 OpenGL 或 Metal,调用 render() 相当于设置着色器,然后调用 glDrawElements() 或 MTLCommandBuffer.commit()。
这是由 render() 执行的渲染管道:
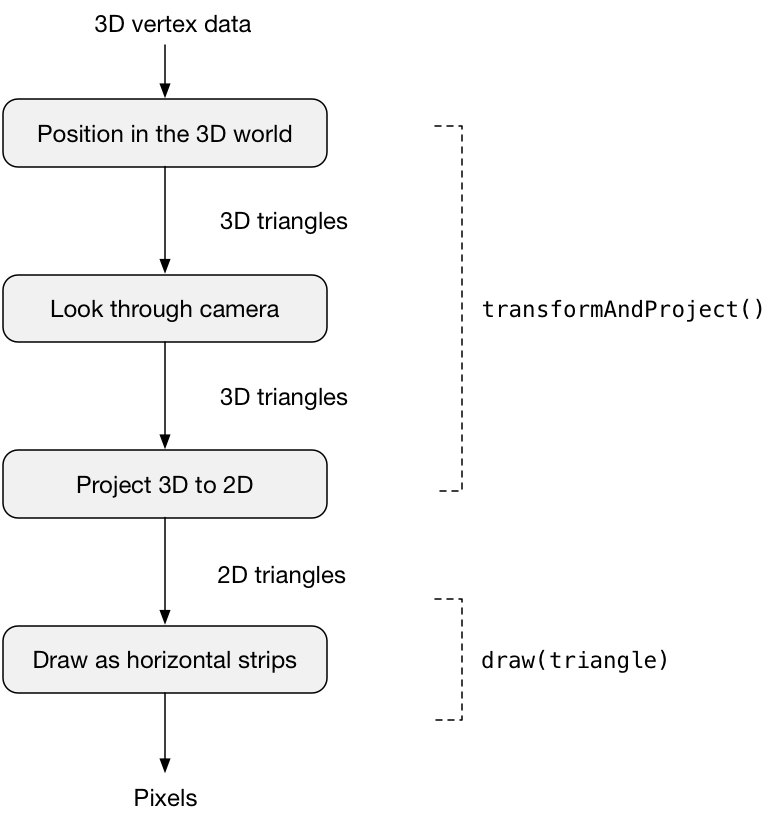
我将详细解释每个步骤中发生的情况。
render() 本身的代码非常简单,因为它将大部分工作交给了辅助函数。 这是代码:
func render() {// 1: Erase what we drew last time.clearRenderBuffer(color: 0xff302010)// 2: Also clear out the depth buffer.for i in 0..<depthBuffer.count {depthBuffer[i] = Float.infinity}// 3: Take the cube, place it in the 3D world, adjust the viewpoint for// the camera, and project everything to two-dimensional triangles.let projected = transformAndProject()// 4: Draw these 2D triangles on the screen.for triangle in projected {draw(triangle: triangle)}
}首先,它删除了在前一帧中绘制的所有内容,以便我们可以从一个干净的平板开始。 (步骤 1 和 2)
然后它调用 transformAndProject()将3D立方体转换为二维三角形列表。 这大致相当于顶点着色器中发生的情况。 (步骤3)
最后,它调用 draw(triangle) 在屏幕上渲染每个 2D 三角形。 这就是片段着色器中发生的情况。 例如,应用照明的计算就是在这里完成的。 (步骤4)
我还没有提到第 2 步中的深度缓冲区。 这用于确保较远的三角形不会与较近的三角形重叠。 深度缓冲区定义为:
var depthBuffer: [Float] = {return [Float](repeating: 0, count: Int(context!.width * context!.height))
}()其中 context!.width 和 .height 是屏幕的大小。 在演示应用程序中,它的大小为 800×600 像素,与渲染缓冲区的大小相同。 为了清除深度缓冲区,我们将其设置为大值 Float.infinity。 稍后我将详细介绍这个深度缓冲区的工作原理。
现在让我们看看步骤 3 中的辅助函数, transformAndProject()。
7、变换三角形
这涉及渲染管线流程图中的前三个操作。
应用程序中的每个 3D 模型(我们只有一个,立方体)都是在其自己的局部坐标空间(也称为模型空间)中定义的。 为了将这些模型绘制到屏幕上,我们必须让它们经历几次“转变”:
- 首先我们必须将模型放置在 3D 世界中。 这是从模型空间到世界空间的转换。 理论上,你已经可以在世界空间坐标中定义立方体,但更容易在其自己的微小宇宙中创建模型,独立于任何其他模型,然后通过平移、缩放和旋转将其放置到更大的世界中。
- 然后我们定位相机并通过该相机观察世界,从世界空间到相机空间(或“眼睛空间”)的转换。 此时,我们已经可以丢弃一些不可见的三角形,因为它们背对相机或因为它们位于相机后面。
- 最后,我们将相机的 3D 视图投影到 2D 表面上,以便我们可以将其显示在屏幕上; 该投影是对屏幕空间(也称为“视口空间”)的转换。
这些转换是所有数学运算发生的地方。 为了弄清楚发生了什么,我将只使用简单的数学—主要是加法、乘法,偶尔也使用正弦和余弦。
注意:在真正的 3D 应用程序中,你会将大部分计算保留在矩阵中,因为它们更加高效且易于使用。 但这些矩阵将执行与你在此处看到的完全相同的操作! 理解数学总是好的,这就是我们手工计算的原因。
TransformAndProject() 中发生的许多事情通常由 GPU 上的顶点着色器完成。 顶点着色器获取模型的顶点并将它们从局部 3D 空间转换为 2D 空间,以及其间的所有步骤。
现在我们将详细研究每一个变换。
8、模型空间到世界空间的变换
在 transformAndProject()函数中,我们首先执行到世界空间的变换。
我们希望立方体能够旋转并上下弹跳。 因此,我们采用定义立方体几何形状的原始顶点(以立方体的本地原点为中心),并将它们从本地模型空间移动到更大的世界中。
对于此转换,我们将使用之前定义的 modelXYZ、modelRotateXYZ、modelScaleXYZ 变量(回想一下,这些是由动画代码更改的变量)。
变换是循环发生的,因为我们需要依次将其应用于模型的每个顶点。 我们将结果存储在一个新的(临时)数组中,因为我们不想覆盖原始的多维数据集数据。 循环看起来像这样:
var transformed = model// Look at each triangle...
for (j, triangle) in transformed.enumerated() {var newTriangle = Triangle()// Look at each vertex of the triangle...for (i, vertex) in triangle.vertices.enumerated() {var newVertex = vertex// TODO: the math happens here// Store the new vertex into the new triangle.newTriangle.vertices[i] = newVertex}// Store the new triangle into the model.transformed[j] = newTriangle
}8.1 本地原点
首先,我们可能需要调整模型的原点,这是一个平移(数学上的意思是“运动”)。 如果 modelOriginX、Y 或 Z 不是 (0, 0, 0),那么我们希望 (modelOriginX, modelOriginY, modelOriginZ) 成为模型的新中心。 我们通过从顶点坐标中减去这些值来做到这一点:
newVertex.x -= modelOriginX
newVertex.y -= modelOriginY
newVertex.z -= modelOriginZ由于顶点的坐标是相对于模型的局部原点的,为了调整这个局部原点,我们需要移动顶点—但方向相反。
8.2 缩放
接下来,我们将应用缩放(如果有)。 如果你从 .obj 文件加载模型并且它不使用与 3D 世界相同的单位(例如米与厘米),则缩放非常有用,但它对于特效也非常有用。 在这个演示中,我们使用缩放来夸大“弹跳”运动。
缩放是一个简单的乘法:
newVertex.x *= modelScaleX
newVertex.y *= modelScaleY
newVertex.z *= modelScaleZ默认情况下 modelScaleX、Y 和 Z 均为 1,因此乘法不起作用。 但如果缩放因子大于1,顶点将远离模型的局部原点,使模型显得更大; 对于小于 1 的缩放因子,顶点将移近原点。
8.3 旋转
接下来是旋转。 这使用了一些三角学知识,但你不需要记住这些公式,我把它们保存在备忘单上。
首先,我们绕 X 轴旋转,然后绕 Y 轴旋转,最后绕 Z 轴旋转。
尽管你需要注意一个称为万向节锁定(gimbal lock)的问题,但执行这些旋转的顺序并不重要。 这基本上意味着,如果你结合某些旋转,你就会迷失方向。 解决这个问题的一种方法是使用更奇特的数学。
// Rotate about the X-axis.
var tempA = cos(modelRotateX)*newVertex.y + sin(modelRotateX)*newVertex.z
var tempB = -sin(modelRotateX)*newVertex.y + cos(modelRotateX)*newVertex.z
newVertex.y = tempA
newVertex.z = tempB// Rotate about the Y-axis:
tempA = cos(modelRotateY)*newVertex.x + sin(modelRotateY)*newVertex.z
tempB = -sin(modelRotateY)*newVertex.x + cos(modelRotateY)*newVertex.z
newVertex.x = tempA
newVertex.z = tempB// Rotate about the Z-axis:
tempA = cos(modelRotateZ)*newVertex.x + sin(modelRotateZ)*newVertex.y
tempB = -sin(modelRotateZ)*newVertex.x + cos(modelRotateZ)*newVertex.y
newVertex.x = tempA
newVertex.y = tempB这些公式围绕模型的调整原点旋转顶点。 这就是为什么区分模型中心和世界中心很重要,因为你不希望顶点围绕整个世界的中心旋转。
注意:因为我们使用的是左手坐标系,所以正旋转是绕旋转轴顺时针旋转。 在右手坐标系中,它将是逆时针方向。
8.4 法向量
回想一下,顶点不仅有 3D 空间中的坐标,还有法向量。 该法线向量描述了顶点(或其三角形)指向的方向。我们需要旋转法线向量,使其与顶点的方向保持对齐。 因为在此演示应用程序中,我们仅绕 Y 轴旋转,所以我仅包含该旋转公式,而不包含其他轴。
tempA = cos(modelRotateY)*newVertex.nx + sin(modelRotateY)*newVertex.nz
tempB = -sin(modelRotateY)*newVertex.nx + cos(modelRotateY)*newVertex.nz
newVertex.nx = tempA
newVertex.nz = tempB8.5 平移
最后,执行到模型在 3D 世界中的目标位置的转换:
newVertex.x += modelX
newVertex.y += modelY
newVertex.z += modelZ好的,这完成了用于在 3D 世界中定位和定向 3D 模型的转换。 现在模型已缩放、旋转并放置在适当的位置。
正如你所看到的,我们正在进行相当多的计算,以使模型从其局部坐标系进入世界空间,并且我们需要对模型中的每个顶点执行这些计算。 如果我们有多个模型(就像大多数游戏所做的那样),我们需要为每个模型重复所有这些计算。
这就是为什么在实践中你会将这些计算放入一个矩阵中,然后你只需将每个顶点与该矩阵相乘即可。 这更简单、更高效,因为它可以进行硬件加速—无论是在 CPU 上通过 simd 指令进行加速,还是在 GPU 上通过顶点着色器进行加速。 通常在 CPU 上计算矩阵,然后将其传递给顶点着色器,顶点着色器将使用它来变换所有顶点。
9、世界空间到相机空间的变换
目前,我们从 (0, 0, 0) 沿 z 轴垂直观察 3D 世界。 但在真正的 3D 应用程序中,观察者可能并不总是处于固定位置。
你可以想象我们正在通过一个“相机”对象观察世界,我们可以将这个相机放置在我们想要的任何地方,并让它看起来像我们想要的任何地方。
这意味着我们需要将对象从“世界空间”转换为“相机空间”。 这使用与之前相同的数学,但方向相反。
for (j, triangle) in transformed.enumerated() {var newTriangle = Triangle()for (i, vertex) in triangle.vertices.enumerated() {var newVertex = vertex// Move everything in the world opposite to the camera, i.e. if the// camera moves to the left, everything else moves to the right.newVertex.x -= cameraXnewVertex.y -= cameraYnewVertex.z -= cameraZ// Likewise, you can perform rotations as well. If the camera rotates// to the left with angle alpha, everything else rotates away from the// camera to the right with angle -alpha. (I did not implement that in// this demo.)newTriangle.vertices[i] = newVertex}transformed[j] = newTriangle}在实践中,你还可以使用矩阵进行相机转换。 事实上,你可以将模型矩阵和相机矩阵组合成一个矩阵,有时称为模型视图(modelview)矩阵。
10、背面剔除
此时,所有三角形都位于“相机空间”中,因此你知道通过相机镜头可以看到世界的哪一部分。
为了节省宝贵的处理时间,你需要丢弃无论如何都不可见的三角形,例如那些位于相机后面或背对相机的三角形。
Metal 或 OpenGL 会自动为你完成此操作。
我没有在演示应用程序中实现它,因为它涉及的数学比我想在这里解释的要多一些,但一种常见的技术是背面剔除(backface culling)。
背面剔除的工作原理是计算相机的方向与三角形面向的方向之间的角度。 这告诉你三角形是指向相机(即可见)还是远离相机(不可见)。 你只需删除面向错误方向的三角形,这样它们就不会被进一步处理。
注意:使用背面剔除时,三角形中顶点的顺序很重要。 如果这个所谓的缠绕顺序错误,你的三角形就根本不会出现! 在这个演示应用程序中,我们不进行面剔除,因此顶点顺序并不重要。
你还可以丢弃相机视野(视锥体:frustum)之外的任何三角形 。但由于这只是一个简单的演示应用程序,因此我也没有实现它。
11、相机空间到屏幕空间的变换
现在我们有一组在相机空间中描述的三角形,它们以三个维度表示。 但我们的计算机屏幕是二维的。 用数学术语来说,我们需要以某种方式将三角形从 3D 投影到 2D。
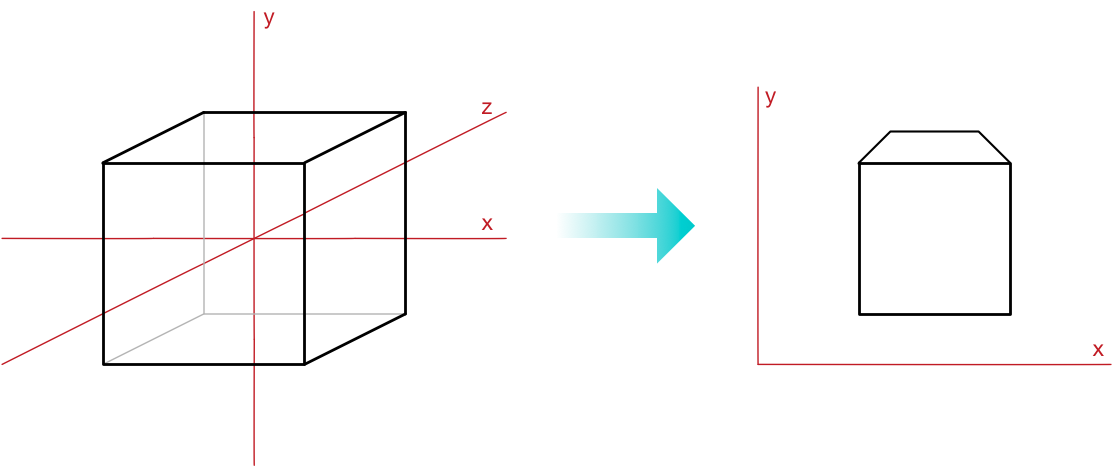
相机空间的单位是你想要的任何单位(我们选择厘米),但我们需要将其转换为像素。
此外,我们需要决定在屏幕上的哪个位置放置相机空间的原点(我们将其放在中心)。 我们必须从 3D 坐标投影到 2D,这需要摆脱 z 轴。
这一切都发生在最后的变换步骤中。
注意:OpenGL 和 Metal 的执行顺序与我们这里的执行顺序略有不同:它们的投影变换将顶点放入“剪辑空间”中,但我们直接将顶点转换为屏幕空间。 在这篇博文中,我主要介绍总体思路,因此请原谅我跳过了一些细节。
和以前一样,我将说明如何使用基本数学运算进行此转换。 通常,你会将所有这些操作组合成一个投影矩阵,并将其传递给顶点着色器,因此将其应用到顶点将发生在 GPU 上。
再次,我们循环遍历所有三角形和所有顶点。 对于每个顶点,我们执行以下操作:
newVertex.x /= (newVertex.z + 100) * 0.01
newVertex.y /= (newVertex.z + 100) * 0.01进行 3D 到 2D 投影的一种简单方法是将 x 和 y 除以 z。 z越大,除法的结果越小。 这是有道理的,因为距离较远的物体应该看起来更小。 在真正的 3D 应用程序中,你将使用更复杂的投影矩阵,但这是总体思路。
注意:为了好玩,请尝试使用这些神奇的数字 100 和 0.01。 通过调整这些数值,你可以获得极端的镜头角度。
我们还需要做两件事。 首先,我们将世界单位(厘米)转换为像素。 在此演示应用程序中,我希望相机视口占据大约 -40 到 +40 的世界单位(厘米)。 我们需要放大顶点的x和y值; 我们在两个方向上使用相同的数量,因此一切都保持正方形:
newVertex.x *= Float(contextHeight)/80
newVertex.y *= Float(contextHeight)/80终于,我们现在开始以像素为单位了!
最后,我们希望 (0, 0) 位于屏幕的中心。 最初它位于右下角,因此将所有内容移动屏幕尺寸的一半(以像素为单位):
newVertex.x += Float(contextWidth/2)
newVertex.y += Float(contextHeight/2)请注意,这些公式仅更改 newVertex.x 和 .y,但不更改 .z。 这是有道理的,因为我们将在屏幕上绘制的三角形现在是二维的。 但我们仍然希望保留这个 z 值。 我们可以用它来填充深度缓冲区,这让我们可以在尝试绘制三角形时确定是否覆盖任何现有像素。
注意:上述内容 - 转换为世界空间、相机空间和屏幕空间 - 是你可以在顶点着色器中执行的操作。 顶点着色器将模型的顶点作为输入,并将它们转换为你想要的任何内容。 你可以像我们在这里所做的那样执行基本操作(平移、旋转、3D 到 2D 投影等),但一切都可以。
这样就完成了转换。 最后我们来画出来吧!
12、三角形光栅化
好的,到目前为止我们所做的就是将 3D 模型放入现实世界中,根据相机的视角进行调整,然后转换为 2D 空间。
我们现在拥有的是相同的三角形列表,但它们的顶点坐标现在代表屏幕上的特定像素(而不是某些想象的三维空间中的点)。
我们可以为每个三角形绘制这三个像素,但这只给我们顶点,它不会填充整个三角形。 为了填充三角形,我们必须以某种方式连接这些顶点像素。 这称为光栅化。
Metal 会为你解决大部分问题。 一旦确定了哪些像素属于三角形,GPU 就会为每个像素调用片段着色器,这样你就可以更改每个像素的绘制方式。
尽管如此,了解光栅化在幕后的工作原理还是很有用的,所以这就是我们将在本节中讨论的内容。
我们需要弄清楚每个三角形由哪些像素组成以及它们的颜色。 这发生在绘制(三角形)中。 render() 函数为屏幕空间中的每个三角形调用 draw(triangle)。
这就是 draw(triangle)函数的作用:
func draw(triangle: Triangle) {// 1. Only draw the triangle if it is at least partially inside the viewport.guard partiallyInsideViewport(vertex: triangle.vertices[0])&& partiallyInsideViewport(vertex: triangle.vertices[1])&& partiallyInsideViewport(vertex: triangle.vertices[2]) else {return}// 2. Reset the spans so that we're starting with a clean slate.spans = .init(repeating: Span(), count: context!.height)firstSpanLine = Int.maxlastSpanLine = -1// 3. Interpolate all the things!addEdge(from: triangle.vertices[0], to: triangle.vertices[1])addEdge(from: triangle.vertices[1], to: triangle.vertices[2])addEdge(from: triangle.vertices[2], to: triangle.vertices[0])// 4. Draw the horizontal strips.drawSpans()
}第 1 步:OpenGL 或 Metal 已经丢弃了所有不可见的三角形。 尽管如此,一些三角形可能只是部分可见。 这些将被裁剪到屏幕的边界。 在此演示应用程序中,我们采用更简单的方法,如果像素落在可见区域之外,则不会绘制像素。
第 2、3、4 步:绘制(三角形)的其余部分会发生什么,我将在下面解释。 请注意,它需要这些附加变量:
var spans = [Span]()
var firstSpanLine = 0
var lastSpanLine = 0为了栅格化三角形,我们将绘制水平条。 例如,如果三角形有这些顶点,
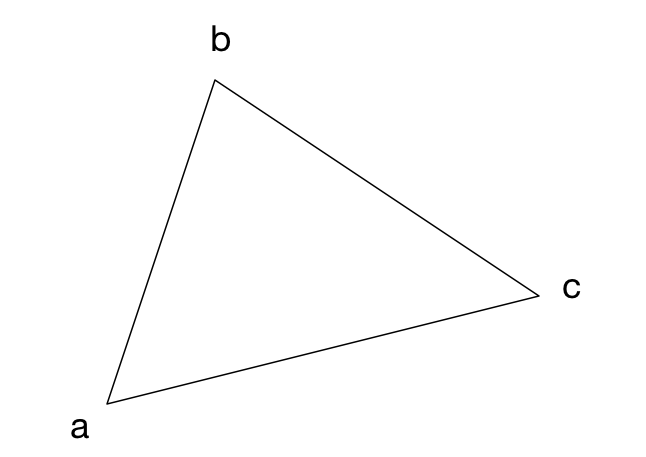
那么水平条将如下所示:
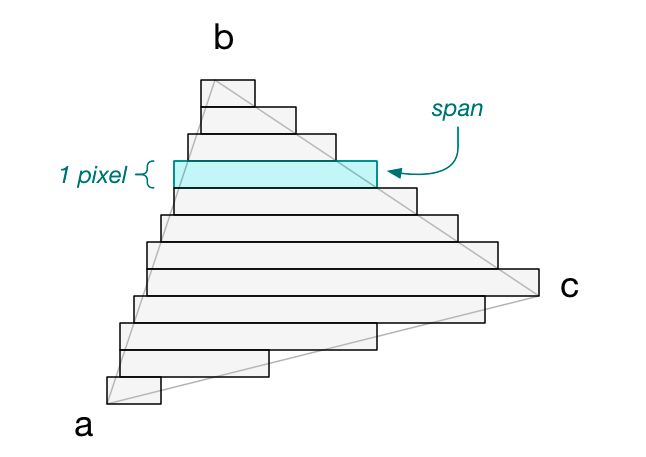
屏幕上的每个垂直位置都有一个条带,因此条带的高度正好是 1 像素。 我将这些水平条带称为跨度(span):
struct Span {var edges = [Edge]()var leftEdge: Edge {return edges[0].x < edges[1].x ? edges[0] : edges[1]}var rightEdge: Edge {return edges[0].x > edges[1].x ? edges[0] : edges[1]}
}为了找出每个跨度的开始和结束位置,我们必须从顶点 a 开始,垂直向顶点 b 移动,以找到每条线上相应的 x 位置。 我们还从顶点 a 到 c,以及从 c 到 b(始终向上)执行此操作。
我们发现的点我称之为边(edge):
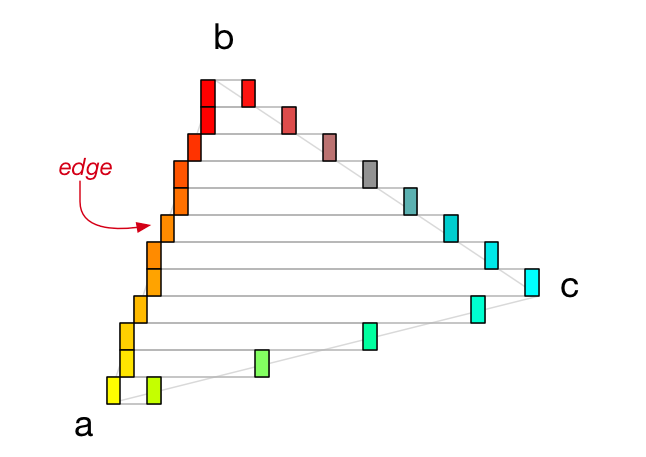
一条边代表一个 x 坐标。 每个跨度都有两个边,一个在左侧,一个在右侧。 一旦找到这两条边,我们只需在它们之间画一条水平线。 对三角形中的所有跨度重复此操作,我们将用像素填充三角形!
struct Edge {var x = 0 // start or end coordinate of horizontal stripvar r: Float = 0 // color at this pointvar g: Float = 0var b: Float = 0var a: Float = 0var z: Float = 0 // for checking and filling in the depth buffervar nx: Float = 0 // interpolated normal vectorvar ny: Float = 0var nz: Float = 0
}光栅化中的关键词是插值。 我们插入所有的东西!
当我们计算这些跨度及其边时,我们不仅会插值顶点的 x 位置,还会插值它们的颜色、法向量、深度缓冲区的 z 值、纹理坐标等等。
对于三角形中的每个像素,我们将为所有这些属性计算一个插值。
顶点属性之间的插值发生在辅助函数 addEdge(from:to:) 中。 下面是这个函数的缩写版本,因为里面有一堆重复的代码。
func addEdge(from vertex1: Vertex, to vertex2: Vertex) {let yDiff = ceil(vertex2.y - 0.5) - ceil(vertex1.y - 0.5)guard yDiff != 0 else { return } // degenerate edgelet (start, end) = yDiff > 0 ? (vertex1, vertex2) : (vertex2, vertex1)let len = abs(yDiff)var yPos = Int(ceil(start.y - 0.5)) // y should be integer because itlet yEnd = Int(ceil(end.y - 0.5)) // needs to fit on a 1-pixel linelet xStep = (end.x - start.x)/len // x can stay floating point for nowvar xPos = start.x + xStep/2let rStep = (end.r - start.r)/lenvar rPos = start.r/* . . . more attributes here . . . */while yPos < yEnd {let x = Int(ceil(xPos - 0.5)) // now we make x an integer too// Don't want to go outside the visible area.if yPos >= 0 && yPos < Int(context!.height) {if yPos < firstSpanLine { firstSpanLine = yPos }if yPos > lastSpanLine { lastSpanLine = yPos }// Add this edge to the span for this line.spans[yPos].edges.append(Edge(x: x, r: rPos, g: . . .))}// Move the interpolations one step forward.yPos += 1xPos += xSteprPos += rStep}
}对其工作原理的快速描述:
我们总是一次只在两个顶点之间进行插值 - 例如上图中从 a 到 b - 因此对于每个三角形,我们必须调用 addEdge(from:to:) 三次。
插值从具有最低 y 坐标 yPos 的顶点到具有最高 y 坐标 yEnd 的顶点。 由于每个跨度代表屏幕上的 1 像素水平线,因此我们在循环的每次迭代中将 yPos 加 1。
对于其他顶点属性,例如 x 位置 (xPos) 和红色分量 (rPos),我们执行简单的线性插值。 在每次迭代中,我们都会给它们增加一些小数值(xStep 和 rStep),以逐渐在它们的起始值和结束值之间移动。
举个例子,如果顶点 a 是黄色,顶点 b 是红色,那么中间的所有点都会慢慢从黄色变成红色。 你可以在图中看到 a 和 b 之间 50% 处的边缘确实是橙色的。
绿色和蓝色、z 位置和法线向量均以相同的方式进行插值。 纹理坐标的行为略有不同,因为你还需要考虑视角。
因此,对于 yPos 的每个值,我们向表示该特定 y 位置的 Span 对象添加一个新的 Edge。 完成后,我们就有了一组 Span 对象,它们描述了组成这个三角形的水平线。 现在我们终于可以推送一些像素了!
OpenGL 和 Metal 将为你完成所有这些插值工作,然后将这些插值值传递给三角形中每个像素的片段着色器。 这就是我们最后一节的主题……
13、最后......绘制三角形
快速提醒一下我们现在所处的位置:我们从一个 2D 三角形列表开始,这些三角形的顶点代表像素坐标。 在上一节中,我们使用 addEdge() 将这些三角形转换为 Span 对象的数组。
每个跨度在屏幕上描述一条水平线。 这条线由两个 Edge 对象定义:每条边都有一个 x 坐标、一个颜色、一个法线向量和一个 z 坐标。 这些都是通过在三角形顶点之间插值来计算的。
函数 drawSpans()将循环遍历Span对象数组,并通过为每个像素调用 setPixel()来绘制水平线。
然而,左边缘的颜色可能与右边缘的颜色不同,因此我们也需要在这些颜色之间进行插值! 第一次我们插值是为了找到三角形边缘的颜色,但这一次我们必须插值来找到穿过三角形的像素的颜色。
水平条带实际上是 1 像素高渐变,如下所示:
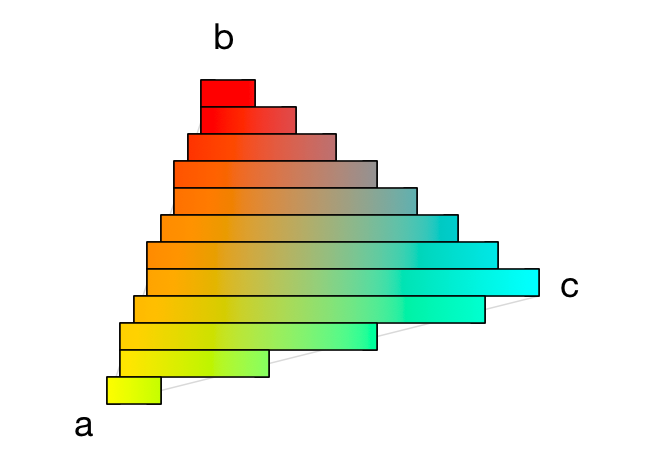
法线向量和 z 位置也是如此:它们也是从左边缘到右边缘进行插值的。
drawSpans() 的代码如下所示:
func drawSpans() {if lastSpanLine != -1 {for y in firstSpanLine...lastSpanLine {if spans[y].edges.count == 2 {let edge1 = spans[y].leftEdgelet edge2 = spans[y].rightEdge// How much to interpolate on each step.let step = 1 / Float(edge2.x - edge1.x)var pos: Float = 0for x in edge1.x ..< edge2.x {// Interpolate between the colors again.var r = edge1.r + (edge2.r - edge1.r) * posvar g = edge1.g + (edge2.g - edge1.g) * posvar b = edge1.b + (edge2.b - edge1.b) * poslet a = edge1.a + (edge2.a - edge1.a) * pos// Also interpolate the normal vector.let nx = edge1.nx + (edge2.nx - edge1.nx) * poslet ny = edge1.ny + (edge2.ny - edge1.ny) * poslet nz = edge1.nz + (edge2.nz - edge1.nz) * pos// TODO: depth buffer// TODO: draw the pixelpos += step}}}}
}你可以看到我们如何从左到右一次步进一个像素并插入颜色和法线向量。
注意:对于立方体中的许多三角形,所有三个顶点都具有相同的法线向量。 因此,这样一个三角形中的所有像素也获得相同的法向量。 但这不是必需的:我还添加了两个三角形(立方体的黄色一侧),它们的顶点具有不同的法线向量,使它们看起来更“圆润”。 你可以清楚地看到黄色边受定向光影响的方式与其他三角形不同。
还有更多,我们将逐步查看。
首先,有深度缓冲区。 这是一个与屏幕尺寸相同 (800×600) 的 Floats 数组。 深度缓冲区可确保较远的三角形不会遮挡距相机较近的三角形。
这是通过将每个三角形像素的 z 值存储到深度缓冲区中来完成的。 如果尚未绘制“较近”的像素,我们仅绘制该像素。 也就是说,只有当 z 值小于当前深度缓冲区中该位置的 z 值时,我们才调用 setPixel() — 这也是 Metal 已经为你提供的功能。
var shouldDrawPixel = true
if useDepthBuffer {let z = edge1.z + (edge2.z - edge1.z) * poslet offset = x + y * Int(context!.width)if depthBuffer[offset] > z {depthBuffer[offset] = z} else {shouldDrawPixel = false}
}注意:演示应用程序还允许你禁用深度缓冲区。 在这种情况下,它将按三角形的平均 z 位置对三角形进行排序,以便首先绘制距离较远的三角形。 然而,这不是一个理想的解决方案,因为它不能保证绘制的三角形不重叠。 (但是如果你的三角形是部分透明的,那么你可能需要使用 z 排序而不是深度缓冲区。)
最后,我们可以绘制像素:
if shouldDrawPixel {let factor = min(max(0, -1*(nx*diffuseX + ny*diffuseY + nz*diffuseZ)), 1)r *= (ambientR*ambientIntensity + factor*diffuseR*diffuseIntensity)g *= (ambientG*ambientIntensity + factor*diffuseG*diffuseIntensity)b *= (ambientB*ambientIntensity + factor*diffuseB*diffuseIntensity)setPixel(x: x, y: y, r: r, g: g, b: b, a: a)
}这就是片段着色器发挥作用的地方。 对于我们必须绘制的每个像素,它都会被调用一次,并带有颜色、纹理坐标、法线向量等的插值。 在这里你可以做各种有趣的事情。
在演示应用程序中,我们根据非常简单的光照模型计算像素的颜色,但你也可以从纹理中采样,或者在将像素颜色写入帧缓冲区之前对像素颜色执行许多其他疯狂的操作。 你可以把它变得像你想象的那样疯狂! 😎
唷! 只是为了在屏幕上得到一个旋转的立方体就需要付出很大的努力。 公平地说,诸如 OpenGL 或 Metal 之类的 API 所做的工作比我们在此介绍的要多得多,而且效率更高,但这从概念上来说就是使用 GPU 绘制 3D 对象时发生的情况。 我希望你觉得它有启发性!
原文链接:无着色器3D渲染 - BimAnt








)





![[密码学]DES](http://pic.xiahunao.cn/[密码学]DES)


)

