文章目录
- 前言
- 一、题目分析
- 二、算法原理
- 1.状态表示
- 2.状态转移方程
- 3.初始化
- 4.填表顺序
- 5.返回值是什么
- 三、代码实现
- 总结
前言
在本文章中,我们将要详细介绍一下Leetcode(面试题 08.01.)三步问题相关的内容
一、题目分析

1.小孩可以上一阶,两阶,三阶
2.对结果取模1000000007就是1e9+7
二、算法原理
1.状态表示
列出dp表,dp表中值的含义是什么

2.状态转移方程
dp[i]是什么
dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
3.初始化
保证填表不会越界
dp[0]=0;
dp[1]=1;
dp[2]=1;
4.填表顺序
从左往右
5.返回值是什么
有多少种上楼方式,dp[i]
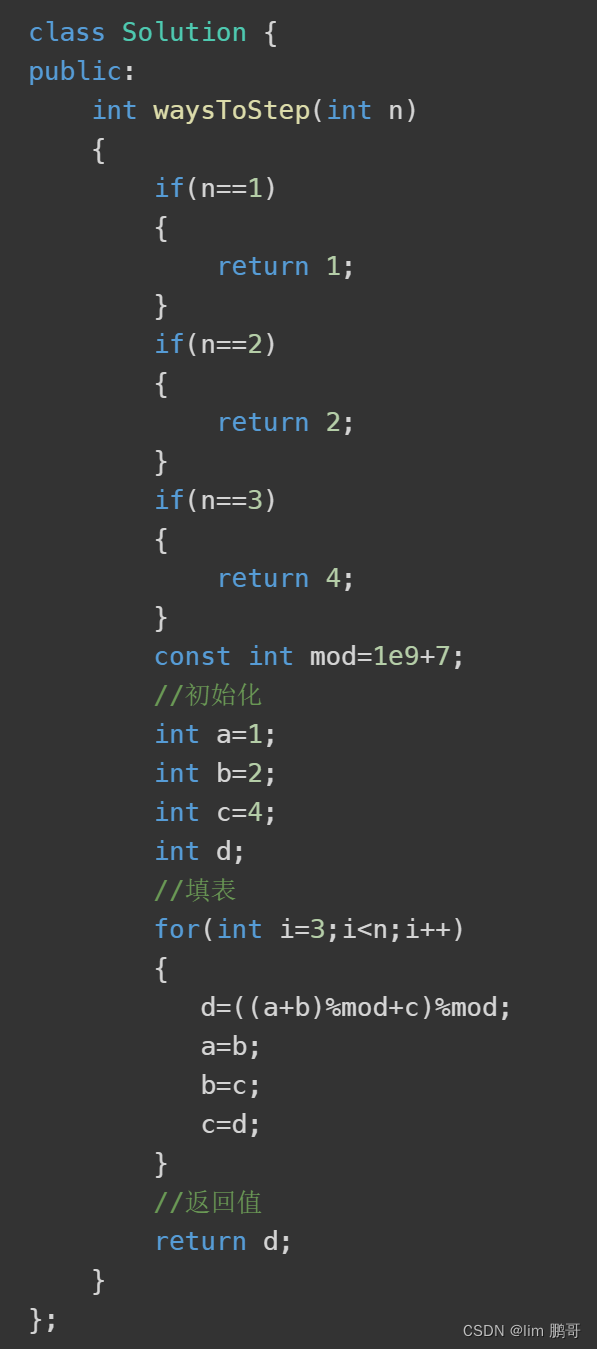
三、代码实现
总结
以上就是我们对Leetcode(面试题 08.01.)三步问题详细介绍,希望对大家的学习有所帮助,仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~



——数据结构与算法)

Spring之循环依赖底层源码解析)

)


)




)



入门教程)