题目描述

有一个长度为n的整数序列。请写一个程序，先把序列中的最小值与第一个数交换，再把最大值与最后一个数交换。输出转换好的序列。 分别编写两个函数MinIndex()和MaxIndex()来计算最小值下标和最大值下标。

int MinIndex(int a[], int n);  //函数返回数组a中最小元素的下标

int MaxIndex(int a[], int n);  //函数返回数组a中最大元素的下标

数组元素的输出调用函数PrintArr()。

---

输入：

输入包括两行。
第一行为正整数n（1≤n≤10）。
第二行为n个正整数组成的序列，保证没有重复元素。

---

输出：

输出转换好的序列。数据之间用空格隔开。

---

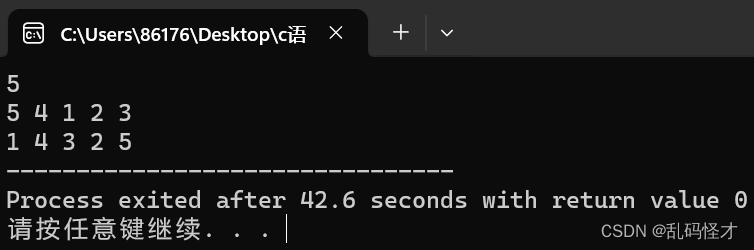
样例输入 Copy

5
5 4 1 2 3

---

样例输出 Copy

1 4 3 2 5

程序代码

#include<stdio.h>
int MinIndex(int a[],int n)//返回最小值下标
{int min=a[0];int flag=0;for(int i=0;i<n;i++){if(min>a[i]){min=a[i];flag=i;}}return flag;
}
int MaxIndex(int a[],int n)//返回最大值下标
{int max=a[0];int flag=0;for(int i=0;i<n;i++){if(max<a[i]){max=a[i];flag=i;}}return flag;
}
void PrintArr(int a[],int n){//输出交换后的数组for(int i=0;i<n;i++){printf("%d ",a[i]);}
}
int main()
{int n;scanf("%d",&n);int a[n];//将序列存入数组中for(int i=0;i<n;i++){scanf("%d",&a[i]);}int t;int min=MinIndex(a,n);//进行最小值和数组中第一个元素交换t=a[0];a[0]=a[min];a[min]=t;int max=MaxIndex(a,n);//进行最大值和数组中最后一个元素交换t=a[n-1];a[n-1]=a[max];a[max]=t;PrintArr(a,n);return 0;
}

运行结果