376. 摆动序列

题目：

连续数字（前减后）的差严格在正负之间交替，差值不能有0为摆动序列。

[1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3)  是正负交替出现的

给定一个整数序列，返回作为摆动序列的最长子序列的“长度”。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

（如果只有两个元素，比如[1,2]或者[2,1]也是摆动序列，[1,1]不知道是不是。）

示例 2:

• 输入: [1,17,5,10,13,15,10,5,16,8]
• 输出: 7
• 解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

思路：

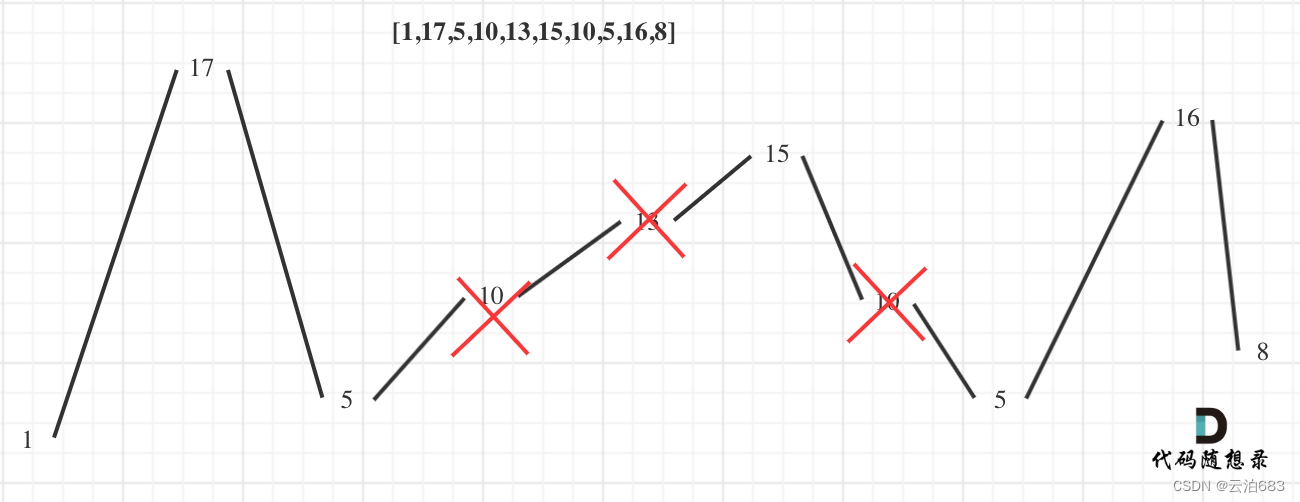
局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。比如5 10 13 15，删掉（10，13）剩下5 15

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

推出最长摆动序列后，要求它的最大长度，就是求就是局部峰值的数量。

程序做法 ：

假如遍历到 i ，计算 前一个的差值 prediff（nums[i] - nums[i-1]） 和 现在的差值 curdiff（nums[i+1] - nums[i]） ，如果 prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。比如17-5-15统计两个波动，1-17-5统计两个波动。

但还有三种情况需要再判断，

1.情况一：上下的坡中有平坡

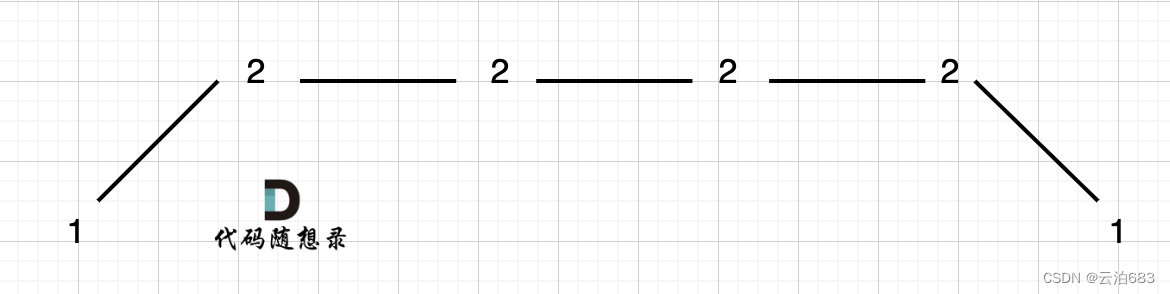
 比如上图，这个时候2-2-2-2，不是摆动序列，上图的实际摆动序列数量只有3个，可以统一删除左边或者右边3个，这里按删掉左边3个来，删掉后，摆动序列数量3，波动1-2，2-1两个。

变成 (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0) 记录一次波动，上图相当于preDiff = 0 && curDiff > 0记录了一次，preDiff >= 0 && curDiff < 0记录了一次，总共两次波动，其他的，proDiff=curDiff=0不记录，相当于删去。

2.情况二：数组首尾两端

我的理解是，数组只有两个的情况

比如[2,5]，这个时候不能统计它的波动，因为preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0 只能判断有3个数字的，但当只有两个，比如[2，5],题目也判断成摆动数组，题目要 求子序列数组判断为摆动数组后的长度，因为被判定为摆动数组，这里的子序列长度是2

所以这种情况怎么处理，可以直接只有两的时候，比如[2，5]判定成2，也可以不增加特殊条件，默认result（波动记录）加个1，为什么result+1呢？因为相当于[2，5]被扩展成了[2，5，5]

满足了之前条件一更新的的preDiff （<）= 0 && curDiff > 0的这个条件，然后result加了个1

总之就是原来result（波动记录）+1，可以计算数组只有两的情况，满足题目，只有两个的数组为摆动数组，长度为2的要求。（所以为了简洁省特殊条件这样整的麻烦吗...）

经过以上分析，代码如下：

// 版本一
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;}preDiff = curDiff;}return result;}
};

疑问1：

但是网站解析上又说数组首尾两端好像不止包含数组只有两个的情况，还包含数组不单只有两个的情况的左右两端的计算，这个我不太明白。

3.情况三：单调坡度有平坡

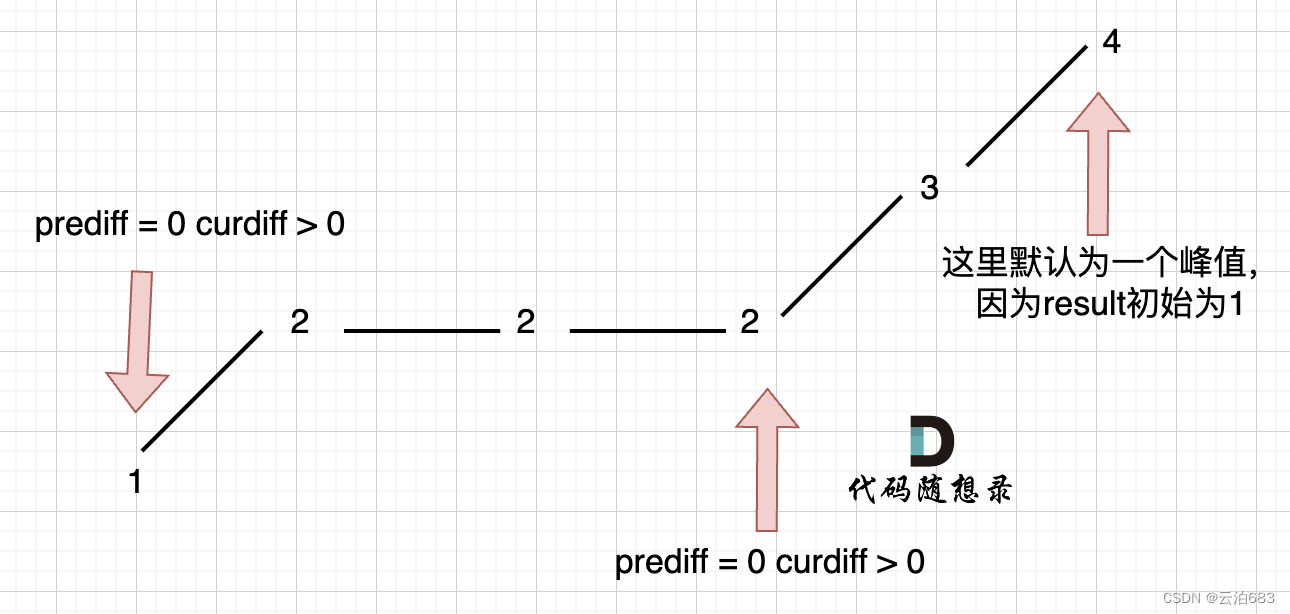
 如上版本一的代码在单调坡度有平坡的情况记录了三个波动（确认为摆动），实际上只有2个摆动，为什么会出现这样的情况呢？实时更新了 prediff。

即preDiff = curDiff;在记录波动，即if（）外面，

为什么实时更新就会出现这样情况呢？

因为实时更新，如上图，prediff=0 curdiff>0导致原来判断情况1：上下的坡中有平坡的条件错判了情况3：单调坡度有平坡的情况了

怎么解决？

不再实时更新，而是当这个坡度 摆动变化的时候，才更新 prediff ，这样单调坡度的时候就不会出现误判情况3：单调坡度有平坡的情况了，

所以为什么这样一改就可以了呢？坡度有变化又是什么意思？

坡度有变化指，满足(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)的条件，result（波动记录）++的时候，没改前会记录上图2-2-2的这个节点，改了后，不会记录这个点，因为从第一个1到2的时候，2往后走就不更新了，一直是prediff>0的状态，这个时候到中间那个2-2-2，就不会更新，因为没更新prediff>0,curdiff>0不满足条件不更新。

总代码：

// 版本二
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;preDiff = curDiff; // 注意这里，只在摆动变化的时候更新prediff}//上一行是和版本一的差别，从外面挪里面了}return result;}
};

总结下就是，序列要满足最长摆动序列的条件的话，就需要求最多的波动点（峰值），而波动点的总值就是序列的子序列and最长摆动序列的长度值。然后有三个不同的条件影响，单调中平坡，上下的坡中平坡，以及强制要求情况，数组首尾两端。

整完后和我想的不一样，3h10min