数值计算
- 第1章 概论
- 1.2 数值计算中的误差
- 1.2.1 误差的来源和分类
- 1.2.2 误差与有效数字
- 1.2.3 数值运算的误差估计
- 1.3 误差定性分析和避免误差危害
- 1.3.1 算法的数值稳定性
- 1.3.3 避免误差危害
- 1.4 数值计算中算法设计的技术
- 1.5 习题
- 1.5.1 判断题
- 1.5.2 计算题
- 第2章 插值法
- 2.2 拉格朗日插值
- 2.3 牛顿插值
- 2.4 埃尔米特插值
- 2.5 分段低次插值
- 2.6 三次样条插值
- 第3章 函数逼近与快速傅里叶变换
- 3.4 曲线拟合的最小二乘法
- 第4章 数值积分与数值微分
- 4.1 数值积分概论
- 4.2 牛顿-柯特斯公式
- 4.3 复合求积公式
- 4.4 龙贝格求积公式
- 4.5 自适应积分方法
- 4.6 高斯求积公式
- 第5章 解线性方程组的直接方法
- 5.2 高斯消去法
- 5.3 矩阵三角分解法
- 5.4 向量和矩阵范数
- 5.5 误差分析
- 第6章 解线性方程组的迭代法
- 6.2 雅可比迭代法与高斯-塞德尔迭代法
- 6.3 超松弛迭代法
- 第7章 非线性方程与方程组的数值解法
- 7.1 方程求根与二分法
- 7.2 不动点迭代法及其收敛性
- 7.3 迭代收敛的加速方法
- 7.4 牛顿法
- 第9章 常微分方程初值问题数值解法
- 9.2 简单的数值方法
第1章 概论
1.2 数值计算中的误差
1.2.1 误差的来源和分类
| 误差类型 | 介绍 | 示例 |
|---|---|---|
| 模型误差 | 在建立数学模型过程中,要将复杂的现象抽象归结为数学模型,往往要忽略一些次要因素的影响,而对问题作一些简化,因此和实际问题有一定的区别。 | 地球的体积使用球体体积公式 v = 4/3 Π R3 来近似计算 |
| 观测误差 | 在建模和具体运算过程中所用的数据往往是通过观察和测量得到的,由于精度的限制,计算这些数据一般是近似的 | 观测地球半径R的值 |
| 截断误差(方法误差) | 当数学模型不能得到精确解时,通常要用数值方法求它的近似解,其近似解与精确解之间的误差称为截断误差或方法误差 | 使用泰勒公式来计算可微函数某点值,其截断误差为泰勒余项 |
| 舍入误差 | 由于计算机字长有限,原始数据在计算机上表示时产生的误差 | Π 用 3.1415926 来近似、4/3 用 1.333333 来近似 |
1.2.2 误差与有效数字
| 误差 | 定义 | 示例 |
|---|---|---|
| 绝对误差(e*) | 设 x 为准确值,x* 为 x 的一个近似值,称 e* = x* - x 为近似值的绝对误差,简称误差 | 一般无法测量出精确值,所以绝对误差一般无法表示 |
| 绝对误差限(ε*) | 估计出绝对误差的一个上界 ε* ,即:| e* | = | x* - x | ≤ ε* | 测量某物品的长度为 20 ± 0.5 cm,则其绝对误差限为 0.5 cm |
| 相对误差( e r ∗ e^*_ {r} er∗) | 绝对误差 精确值 ,即: e r ∗ = e ∗ x = x ∗ − x x \frac{绝对误差}{精确值},即:e^*_ {r}=\frac{e^*}{x}=\frac{x^*-x}{x} 精确值绝对误差,即:er∗=xe∗=xx∗−x 实际中精确值 x 是未知的,故常用 绝对误差 近似值 ,即: e r ∗ = e ∗ x ∗ = x ∗ − x x ∗ \frac{绝对误差}{近似值} ,即:e^*_ {r}=\frac{e^*}{x^*}=\frac{x^*-x}{x^*} 近似值绝对误差,即:er∗=x∗e∗=x∗x∗−x | 当 e r ∗ e^*_ {r} er∗ 较小时,此时 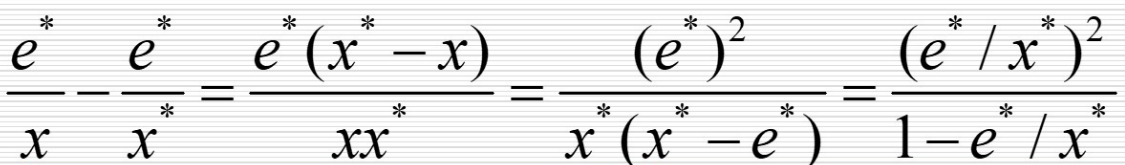 是 e r ∗ 的平方项级,故可以忽略不计,所以可以使用 e ∗ x ∗ 代替 e ∗ x 是 e^*_ {r} 的平方项级,故可以忽略不计,所以可以使用 \frac{e^*}{x^*} 代替 \frac{e^*}{x} 是er∗的平方项级,故可以忽略不计,所以可以使用x∗e∗代替xe∗ 是 e r ∗ 的平方项级,故可以忽略不计,所以可以使用 e ∗ x ∗ 代替 e ∗ x 是 e^*_ {r} 的平方项级,故可以忽略不计,所以可以使用 \frac{e^*}{x^*} 代替 \frac{e^*}{x} 是er∗的平方项级,故可以忽略不计,所以可以使用x∗e∗代替xe∗ |
| 相对误差限( ε r ∗ ε^*_ {r} εr∗) | 相对误差的上界 ε r ∗ ε^*_ {r} εr∗,即: ε r ∗ = ε ∗ ∣ x ∗ ∣ ε^*_ {r} = \frac{ε^*}{|x^*|} εr∗=∣x∗∣ε∗ | 测量某物品的长度为 20 ± 0.5 cm,则其相对误差限为 2.5% |
| 有效数字 | 示例 | |
|---|---|---|
| 定义 |  | 对于 Π=3.1415926… ,x* = 3.14有3位有效数字;x* = 3.1416 则有5为有效数字;而 x* = 3.1415 则只有4为有效数字,其误差超过了5所在位置的半个单位,而不超过1所在的位置的半个单位,故只有4位有效数字。 |
| 科学计数表示 |  | 12300 有5位有效数字,如果写成 1.23 × 104 则只有3位有效数字。 |
| 定理 |  |  |
1.2.3 数值运算的误差估计
| 函数 | (绝对)误差限 ε ∗ ( f ) ≈ ε^*( f )≈ ε∗(f)≈ | 相对误差限 ε r ∗ ( f ) ≈ ε^*_r( f )≈ εr∗(f)≈ |
|---|---|---|
| 一元函数 f(x) | | f(x)’ | ε*(x) | ε*( f(x) ) / f(x) |
| 多元函数 f(x1, …, xn) | ∑ 1 n ∣ ∂ f ∂ x i ∣ ε ∗ ( x i ) \sum_1^n |\frac{\partial f}{\partial x_i}| ε^*(x_i) 1∑n∣∂xi∂f∣ε∗(xi) | ε*( f(x1, …, xn) ) / f(x1, …, xn) |
示例:

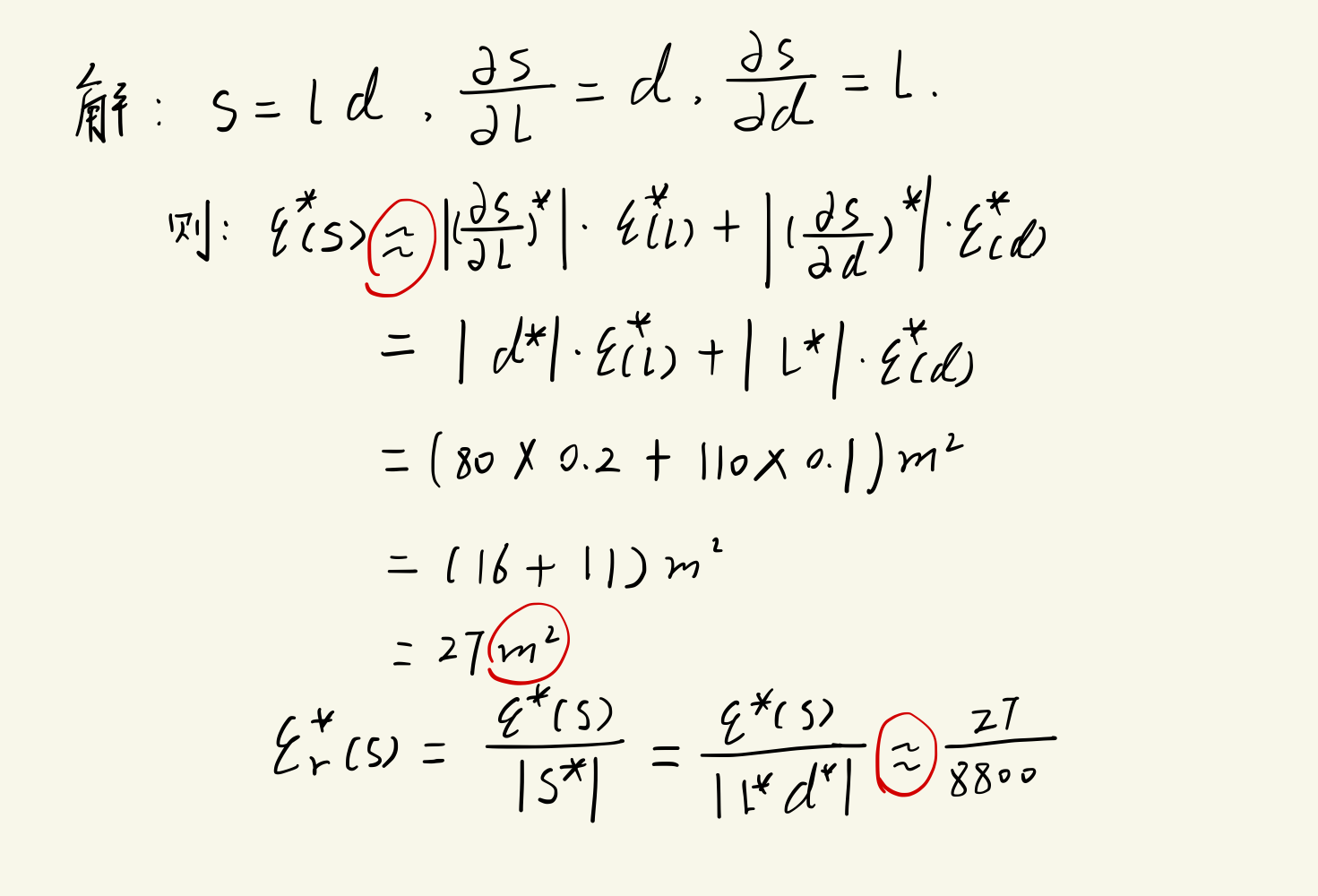
1.3 误差定性分析和避免误差危害
1.3.1 算法的数值稳定性
| 问题 | 描述 |
|---|---|
| 不稳定算法 |  |
| 病态方程组 |  |
1.3.3 避免误差危害
| 问题 | 描述 | 措施 |
|---|---|---|
| 大数吃小数 |  |  |
| 相近数相减 |  |  例如: 1 − c o s ( ε ) = 2 s i n 2 ( ε 2 ) ; 例如:1 - cos(ε) = 2 sin^2(\frac{ε}{2}) ; 例如:1−cos(ε)=2sin2(2ε); 例如: 1 − c o s ( ε ) = 2 s i n 2 ( ε 2 ) ; 例如:1 - cos(ε) = 2 sin^2(\frac{ε}{2}) ; 例如:1−cos(ε)=2sin2(2ε);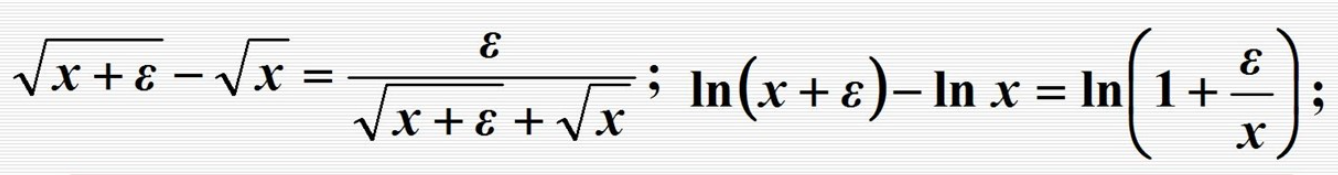 |
| 除小数和乘大数 | 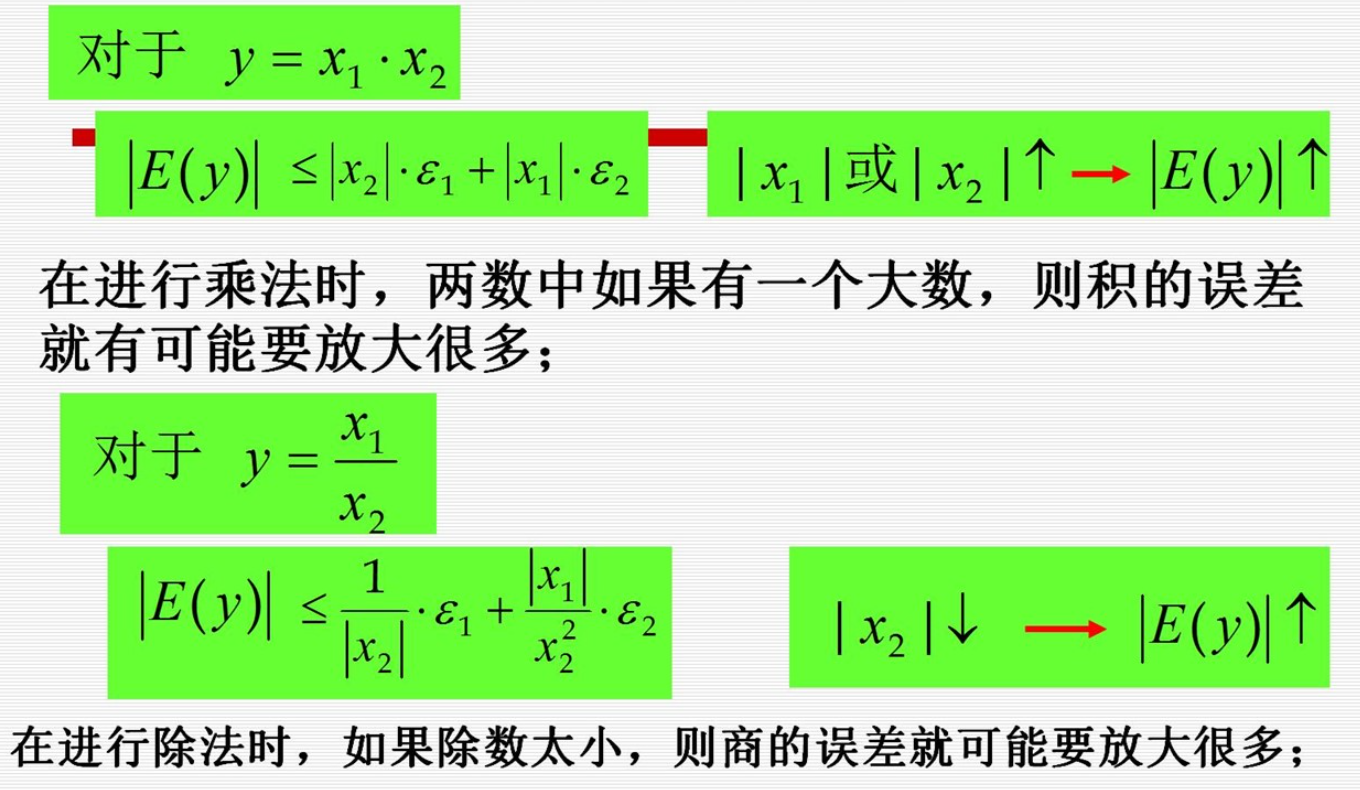 | 尽量避免 |
1.4 数值计算中算法设计的技术
| 算法 | 示例 |
|---|---|
| 快速幂算法 |  |
| 秦九韶算法 |  |
1.5 习题
1.5.1 判断题
- 解对数据的微小变化高度敏感是病态的。【对】
- 高精度运算可以改善问题的病态性。【错,病态是问题本身固有的,无法通过提高精度运算来改善】
- 无论问题是否病态,只要算法稳定都能得到好的近似值。【错,只有良态情况下,稳定的算法才有可能得到好的近似值】
- 用一个稳定的算法计算良态问题一定会得到好的近似值。【错,得到好的近似值还与初始值的选取有关,例如:牛顿法】
- 用一个收敛的迭代法计算良态问题一定会得到好的近似值。【错,得到好的近似值还与初始值的选取有关,例如:牛顿法】
- 两个相近数相减必然会使有效数字损失。【错,只是大多情况下会使有效数字损失】
- 计算机上将1000个数量级不同的数相加,不管次序如何结果都是样的。【错,可能发生大数吃小数情况】
1.5.2 计算题
- 设 x > 0,x 的相对误差为δ,求ln x的误差。
- 设 x 的相对误差为2%,求 xn 的相对误差。
- 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:
x 1 ∗ x^*_1 x1∗= 1.1021, x 2 ∗ x^*_2 x2∗= 0.031, x 3 ∗ x^*_3 x3∗= 385.6, x 4 ∗ x^*_4 x4∗= 56.430, x 5 ∗ x^*_5 x5∗=7 × 1.0 - 求下列各近似值的误差限:
(1) x 1 ∗ + x 2 ∗ + x 4 ∗ x^*_1+x^*_2+x^*_4 x1∗+x2∗+x4∗
(2) x 1 ∗ x 2 ∗ x 3 ∗ x^*_1x^*_2x^*_3 x1∗x2∗x3∗
(3) x 2 ∗ / x 4 ∗ x^*_2/x^*_4 x2∗/x4∗
其中 x 1 ∗ , x 2 ∗ , x 3 ∗ , x 4 ∗ x^*_1,x^*_2,x^*_3,x^*_4 x1∗,x2∗,x3∗,x4∗均为第3题所给的数。 - 计算球体积要使相对误差限为1%,问度量半径R时允许的相对误差限是多少?
- 正方形的边长大约为100 cm,应怎样测量才能使其面积误差不超过1 cm2 ?
- 计算 f = ( 2 − 1 ) 6 f=(\sqrt{2}-1)^6 f=(2−1)6,取 2 ≈ 1.4 \sqrt{2}≈1.4 2≈1.4,利用下列等式计算,哪一个得到的结果最好?
1 ( 2 + 1 ) 6 , ( 3 − 2 2 ) 3 \frac{1}{(\sqrt{2}+1)^6},(3-2\sqrt{2})^3 (2+1)61,(3−22)3
1 ( 3 + 2 2 ) 3 , 99 − 70 2 \frac{1}{(3+2\sqrt{2})^3},99-70\sqrt{2} (3+22)31,99−702













覆盖优化 - 附代码)
-标签管理)







