目录
4.二叉树链式结构的操作
4.1 前置说明
4.2二叉树的遍历
4.2.1 前序、中序以及后序遍历
4.3 节点个数以及高度等
4.二叉树链式结构的操作
4.1 前置说明
由于博主对二叉树的结果掌握还不够深入,因此在讲解相关操作前将手动创建一颗简单的二叉树,快速进入正题,等博主二叉树结构了解的差不多时,我将会进行内容补充。
typedef struct TreeNode
{int data;struct TreeNode* left;struct TreeNode* right;
}TreeNode;TreeNode* CreateNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));node->data = x;node->left = NULL;node->right = NULL;return node;
}
TreeNode* node1 = CreateNode(1);
TreeNode* node2 = CreateNode(2);
TreeNode* node3 = CreateNode(3);
TreeNode* node4 = CreateNode(4);
TreeNode* node5 = CreateNode(5);
TreeNode* node6 = CreateNode(6);node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;TreeNode* root = node1; 注意:上述代码 并不是创建二叉树的方式 ,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念, 二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的。
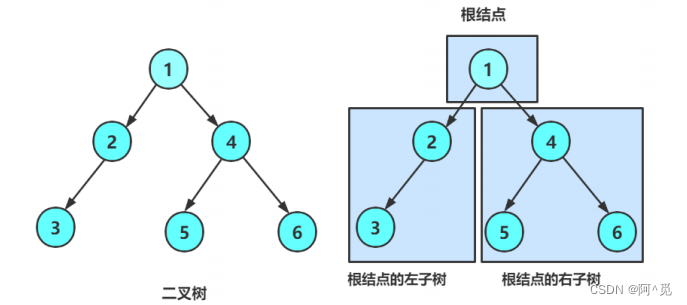
从概念中可以看出,二叉树定义是 递归式 的,因此后序基本操作中基本都是按照该概念实现的。
4.2二叉树的遍历
4.2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓 二叉树遍历 (Traversal) 是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次 。
访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有: 前序 / 中序 / 后序的递归结构遍历 :1. 前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中(间)。3. 后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根, 所以 N(Node )、 L(Left subtree )和 R(Right subtree )又可解释为 根、根的左子树和根的右子树 。 NLR 、 LNR 和 LRN 分别又称为 先根 遍历、 中根 遍历和 后根 遍历。
下面主要分析 前序 递归遍历,中序与后序图解类似,伙伴们可以自己动手绘制。
前序遍历递归图解 :
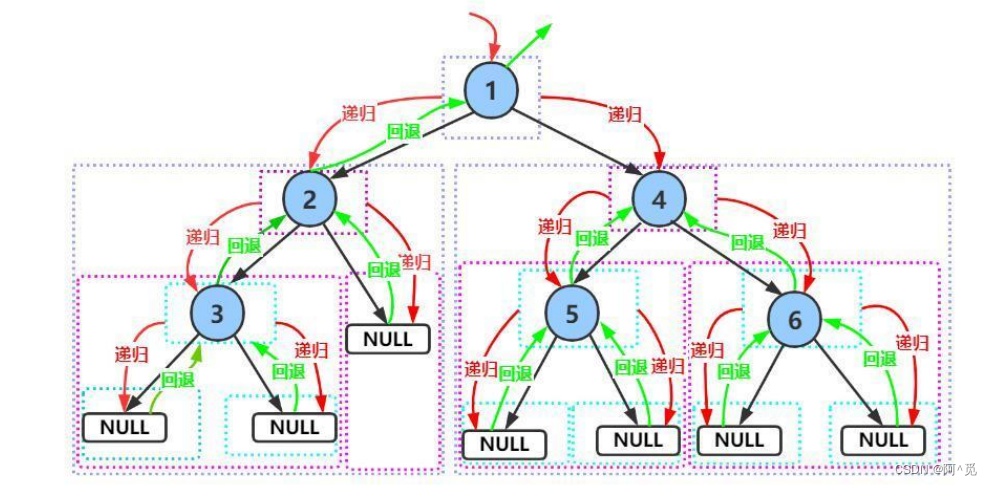
切记:初次学习一定要画递归展开图便于自己更深入理解递归
下面是实例测试代码(仅供参考):
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef struct TreeNode
{int data;struct TreeNode* left;struct TreeNode* right;
}TreeNode;TreeNode* CreateNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));node->data = x;node->left = NULL;node->right = NULL;return node;
}//前序遍历
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}//中序遍历
void InOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}PrevOrder(root->left);printf("%d ", root->data);PrevOrder(root->right);
}//后序遍历
void PostOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}PrevOrder(root->left);PrevOrder(root->right);printf("%d ", root->data);
}void test01()
{//创树TreeNode* node1 = CreateNode(1);TreeNode* node2 = CreateNode(2);TreeNode* node3 = CreateNode(3);TreeNode* node4 = CreateNode(4);TreeNode* node5 = CreateNode(5);TreeNode* node6 = CreateNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;TreeNode* root = node1;//前序遍历PrevOrder(root);printf("\n");//中序遍历InOrder(root);printf("\n");//后序遍历PostOrder(root);printf("\n");}int main()
{test01();return 0;
}4.3 节点个数以及高度等
1..计算高度:
//方法一
int TreeHeight(TreeNode* root)
{return TreeHeight(root->left) > TreeHeight(root->right) ?TreeHeight(root->left) + 1 :TreeHeight(root->right) + 1;
}//方法二
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;
}由于方法一中比较时就开始递归了,却没有记录数据,导致后一条语句又要进行递归遍历,非常耗时间,因此用第二种方法更好
2.计算总结点个数:
int TreeSize(TreeNode* root)
{return root == NULL ? 0 :TreeSize(root->left) +TreeSize(root->right) + 1;}此为三目操作符的运用
3.计算第k层的节点个数:
int TreeKSize(TreeNode* root,int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return TreeKSize(root->left, k - 1)+ TreeKSize(root->right, k - 1);
}4.叶节点个数:
int TreeLeafSize(TreeNode* root)
{if (root == NULL)return 0;if (root->left == NULL&& root->right == NULL)return 1;return TreeLeafSize(root->left) +TreeLeafSize(root->right);
}







)










)
