算法效率的度量

算法效率的度量通常是通过时间复杂度和空间复杂度来描述的。

一、时间复杂度

算法中所有语句的执行次数之和为T(n)，它是算法问题规模n的函数，时间复杂度主要分析T(n)的数量级。

分类

1. 最好时间复杂度：最好情况下，算法的时间复杂度。

2. 平均时间复杂度：所有可能输入实例在等概率出现的情况下，算法的期望运行时间。

3. 最坏时间复杂度：最坏情况下，算法的时间复杂度（一般总是考虑算法在最坏情况下的时间复杂度）。

常见的渐进时间复杂度为

$O(1)<O(log_{2}n)<O(n)<O(nlog_{2}n)<O(n^{2})<O(2^{n})<O(n!)<O(n^{n})$

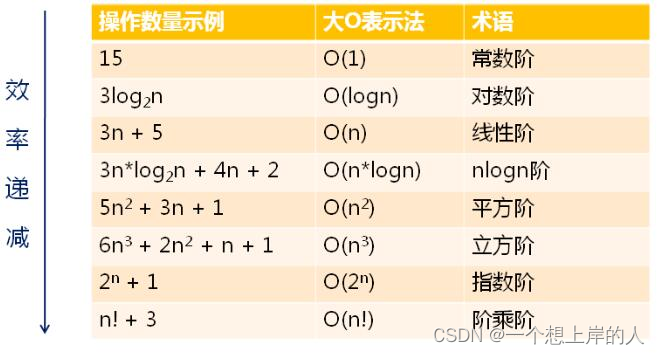
二、空间复杂度

算法的空间复杂度S(n)定义为该算法所耗费的存储空间，它是问题规模n的函数。

提示：算法原地工作是指算法所需的辅助空间为常量，即O(1)。

三、计算规则

加法规则： $O(f(n))+O(g(n))=O(max(f(n), g(n))$

乘法规则： $O(f(n)) \times O(g(n)) = O(f(n) \times g(n))$

另外，还有算法的实际运行时间和资源利用率也作为度量算法效率的描述。

算法的实际运行时间：除了理论上的时间复杂度外，实际运行时间也是衡量算法效率的重要指标。通过实际测试或者分析算法的执行次数来得出算法的实际运行时间。

算法的资源利用率：算法的资源利用率包括CPU利用率、内存利用率等，描述了算法在执行过程中对计算机资源的利用程度。

以上指标可以根据具体的应用场景来选择和权衡，综合考虑可以得出算法的效率评估。

四、举个栗子

以下是一个示例题目，涉及到算法效率的评估：

题目：给定一个包含n个整数的列表，设计一个算法来计算列表中所有整数的和。

解答：可以使用两种算法来计算列表中所有整数的和，并比较它们的效率。

算法一：遍历求和

遍历列表中的每个元素，将其累加到一个变量中。
最后返回累加的结果作为列表的和。

以下是一个示例代码（Python）：

def sum_of_list(nums):total = 0for num in nums:total += numreturn total# 示例用法
my_list = [1, 2, 3, 4, 5]
result = sum_of_list(my_list)
print(result)  # 输出15

算法二：数学公式求和

使用数学公式求解整数序列的和，即使用高斯求和公式 Sn = n * (n+1) / 2，其中 n 是列表中整数的个数。
将列表的长度代入公式得到结果。

以下是一个示例代码（Python）：

def sum_of_list(nums):n = len(nums)total = n * (n + 1) // 2return total# 示例用法
my_list = [1, 2, 3, 4, 5]
result = sum_of_list(my_list)
print(result)  # 输出15

效率评估：