一.题干
迷宫有一个入口,一个出口。一个人从入口走进迷宫,目标是找到出口。阴影部分和迷宫的外框为墙,每一步走一格,每格有四个可走的方向,探索顺序为地图方向:南(下)、东(右)、北(上)、西(左)。
输入:输入迷宫数组。第一行数据表示一个 n*n (n<=100)的迷宫;第二行开始的n行为迷宫数据。
其中:0表示路,1表示墙,起点在左上角 <1,1> 的位置,终点在右下角 <n,n> 的位置。
输出:若有解,输出从入口到出口的一条路径,否则输出 there is no solution!
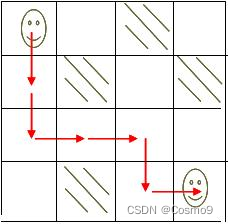
例(上图所示的迷宫数组)
输入:
4 4
0 0 1 0
0 1 0 1
0 0 0 0
0 1 0 0
输出:<1,1> <2,1> <3,1> <3,2> <3,3> <4,3> <4,4>
| 测试输入 | 期待的输出 | 时间限制 | 内存限制 | 额外进程 | |
|---|---|---|---|---|---|
| 测试用例 1 | 以文本方式显示
| 以文本方式显示
| 1秒 | 64M | 0 |
| 测试用例 2 | 以文本方式显示
| 以文本方式显示
| 1秒 | 64M | 0 |
二.题目分析
我们知道,迷宫问题其实就是连通图的遍历。那么显然地,可以使用BFS;采用BFS的话有个好处,第一条即为最短路径,按照出题人的想法应该就是采用BFS。试一下
很好,要用DFS,没要求最短,好好好,这么写,就是想考一下DFS是吧(气急败坏了已经)
三,代码如下:
(使用的递推实现的DFS,也可以用递归,形式上更为简洁)
#include <iostream>
#include <stack>
using namespace std;
struct Point
{int col;int row;Point(int r, int c) : row(r), col(c) {}bool operator!=(const Point &p) const{return this->row != p.row || this->col != p.col;}
};
Point getNVnode(bool **mark, Point p, int m, int n)
{if (p.row + 1 < m && !mark[p.row + 1][p.col]) // 下return Point(p.row + 1, p.col);if (p.col + 1 < n && !mark[p.row][p.col + 1]) // 右return Point(p.row, p.col + 1);if (p.row - 1 >= 0 && !mark[p.row - 1][p.col]) // 上return Point(p.row - 1, p.col);if (p.col - 1 >= 0 && !mark[p.row][p.col - 1]) // 左return Point(p.row, p.col - 1);return Point(-1, -1);
}
void DFSpath(void *maze, int m, int n, const Point &startP, Point endP, stack<Point> &pointStack)
{int **maze2d = new int *[m];for (int i = 0; i < m; ++i)maze2d[i] = (int *)maze + i * n;bool **mark = new bool *[m];for (int i = 0; i < m; ++i){mark[i] = new bool[n];for (int j = 0; j < n; ++j)mark[i][j] = *((int *)maze + i * n + j);}pointStack.push(startP);mark[startP.row][startP.col] = true;while (pointStack.empty() == false && pointStack.top() != endP){Point NextP = getNVnode(mark, pointStack.top(), m, n);if (NextP.row == -1){pointStack.pop();continue;}mark[NextP.row][NextP.col] = true;pointStack.push(NextP);}
}int main()
{int N;cin >> N >> N;if (N == 1)printf("<1,1> \n");int maze[N][N];for (int i = 0; i < N; ++i)for (int j = 0; j < N; ++j)cin >> maze[i][j];Point startP(0, 0);Point endP(N - 1, N - 1);stack<Point> pointStack;DFSpath(maze, N, N, startP, endP, pointStack);if (pointStack.empty() == true)cout << "There is no solution!" << endl;else{stack<Point> tmpStack;while (pointStack.empty() == false){tmpStack.push(pointStack.top());pointStack.pop();}while (tmpStack.empty() == false){cout<<"<"<<tmpStack.top().row+1<<" "<<tmpStack.top().col+1<<"> ";tmpStack.pop();}cout << endl;}
}



)




-settings)









