0 提纲
- 噪声相关概述
- 噪声处理的理论与方法
- 基于数据清洗的噪声过滤
- 主动式过滤
- 噪声鲁棒模型
1 噪声相关概述
噪声类型:
- 属性噪声:样本中某个属性的值存在噪声
- 标签噪声:样本归属类别
关于噪声分布的假设:均匀分布、高斯分布、泊松分布等。
标签噪声的产生原因:
(1)特定类别的影响,在给定的标注任务中,各个类别样本之间的区分度不同,有的类别与其他类别都比较相似,就会导致这类样本标注错误率高。
(2)标注人为的因素。
(3)少数类的标注更容易错误。
(4)训练数据受到了恶意投毒,当在对抗环境下应用机器学习模型时,攻击者往往会通过一些途径向数据中注入恶意样本,扰乱分类器的性能。
噪声标签的影响:
- 标签噪声比属性噪声更重要
- 数据利用率
- 分类性能下降: k k kNN、决策树和支持向量机、 Boosting 等。
- 模型复杂度
– 决策树节点增多
– 为了降低噪声影响,需要增加正确样本数量
– 可能导致非平衡数据 - 正面影响:Bagging训练数据中的噪声有利于提升基分类器的多样性
与噪声类似的概念和研究:
- 异常
- 离群点:outlier
- 少数类
- 小样本
- 对抗样本
- 恶意样本
- 脏数据
2 噪声处理的理论与方法
2.1 噪声处理的理论基础
概率近似正确定理(probably approximately correct,PAC ):
对于任意的学习算法而言,训练数据噪声率 β \beta β,必须满足 β ≤ ε / ( 1 + ε ) β≤ ε /(1+ ε) β≤ε/(1+ε) ,其中 ε ε ε表示分类器的错误率。
2.2 噪声处理的方法概览
- 基于数据清洗的噪声过滤
- 主动式噪声过滤
- 噪声鲁棒模型
3 基于数据清洗的噪声过滤
数据层
- 去除噪声样本
- 修正噪声样本
- 方法:采用噪声敏感方法检测噪声
– k k kNN, k k k小
– 密度方法
– 决策树
– 集成学习:静态集成、动态集成;投票
– 主动学习:人工+分类器迭代
直接删除:
- 直接删除法是基于两种情况,把异常值影响较大或看起来比较可疑的实例删除,或者直接删除分类器中分类错误的训练实例。
- 在具体实现方法上,如何判断异常值、可疑等特征,可以使用边界点发现之类的方法。
基于最近邻的去噪方法:
- 从 k k kNN本身原理来看,当 k k k比较小的时候,分类结果与近邻的样本标签关系很大。因此,它是一种典型的噪声敏感模型,在噪声过滤中有一定优势。
- 压缩最近邻CNN、缩减最近邻RNN、基于实例选择的Edited Nearest Neighbor等,也都可以用于噪声过滤。
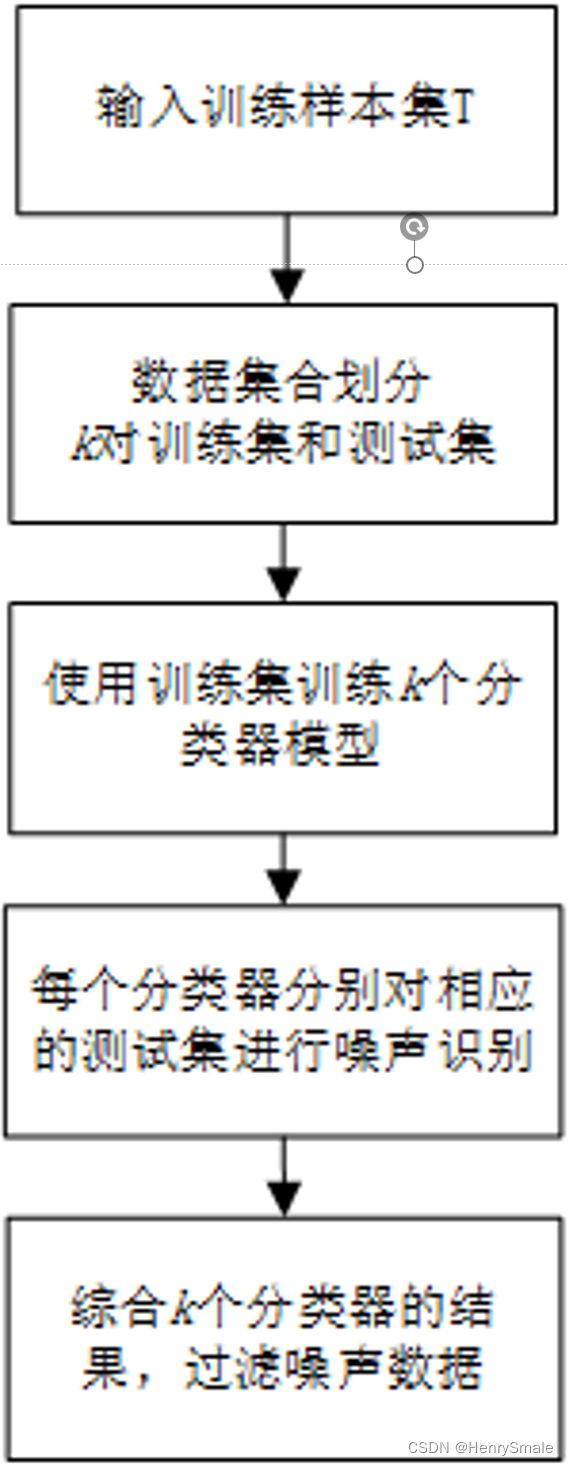
集成去噪:集成分类方法对若干个弱分类器进行组合,根据结果的一致性来判断是否为噪声,是目前一种较好的标签去噪方法。两种情况:
- 使用具有相同分布的其他数据集,当然该数据集必须是一个干净、没有噪声的数据。
- 不使用外部数据集,而是直接使用给定的标签数据集进行 K K K折交叉分析。
4 主动式过滤
主动式过滤:
- 基于数据清洗的噪声过滤方法的隐含假设是噪声是错分样本,把噪声和错分样本等同起来。
- 位于分类边界的噪声最难于处理,需要人工确认。
主动学习框架和理论为人类专家与机器学习的写作提供了一种有效的途径,它通过迭代抽样的方式将某种特定的样本挑选出来,交由专家对标签进行人工判断和标注,从而构造有效训练集的一种方法。
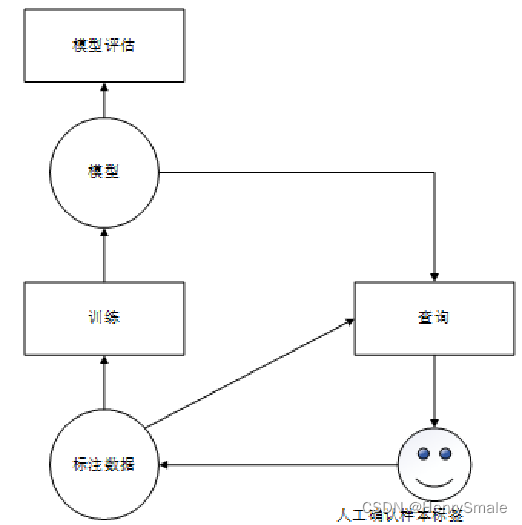
查询策略如何选择可能是噪声的样本,就成为主动学习的核心问题。
查询策略主要可以分为以下两类:
- 基于池的样例选择算法;
- 基于流的样例选择算法。
基于池的样本选择算法代表性的有:
- 基于不确定性采样的查询方法;
- 基于委员会的查询方法;
- 基于密度权重的方法等。
不确定性采样的查询:将模型难于区分的样本提取出来,具体在衡量不确定性时可以采用的方法有最小置信度、边缘采样和熵。

x L C ∗ = argmax x ( 1 − P θ ( y ^ ∣ x ) ) = argmin x P θ ( y ^ ∣ x ) x_{L C}^{*}=\operatorname{argmax}_{x}\left(1-P_{\theta}(\hat{y} \mid x)\right)=\operatorname{argmin}_{x} P_{\theta}(\hat{y} \mid x) xLC∗=argmaxx(1−Pθ(y^∣x))=argminxPθ(y^∣x)
边缘采样是选择哪些类别概率相差不大的样本:
x M ∗ = argmin x ( P θ ( y ^ 1 ∣ x ) − P θ ( y ^ 2 ∣ x ) ) x_{M}^{*}=\operatorname{argmin}_{x}\left(P_{\theta}\left(\hat{y}_{1} \mid x\right)-P_{\theta}\left(\hat{y}_{2} \mid x\right)\right) xM∗=argminx(Pθ(y^1∣x)−Pθ
![[SQL挖掘机] - 窗口函数 - dense_rank](http://pic.xiahunao.cn/[SQL挖掘机] - 窗口函数 - dense_rank)


)
)



从入门到精通系列之四:K8s的基本概念和术语之集群类)







)


