以下内容纯属个人学习记录,难免有误,欢迎指正~
引子
虽已工作数宰,但当因为工作的需要再次碰到傅里叶级数/变换相关的知识时是还是难免汗流浃背,读书时的痛苦的回忆涌上心头,果然曾经欠下的总归是要偿还的,那么这次就和它们做一次了断吧。
读书时对傅里叶级数/变换的恐惧主要在于两点:
① 被傅里叶级数/变换公式中,代表无穷的求和符合∑和积分∫符号吓得两股战战(根本原因在于微积分没学好,晕微积分),难以理解各种不同的信号怎么就能统一地这种无穷的函数组合形式来表达? ② 傅里叶级数/傅里叶变换中的函数单元组合为什么是正余弦函数?
直到最近再次捡起微积分的课本,又有幸拜读了几篇神作,摸到了微积分的内在逻辑和科学思想的一点门槛,基于此再次回首傅里叶级数/变换,竟有种“柳暗花明又一村”的顿悟,于是针对上述问题有了一个阶段性的答案,且听我娓娓道来。
傅里叶级数/变换背后的隐藏大佬——微积分
针对问题①,我的解答如下
傅里叶级数/变换公式的形式和其背后的逻辑思想源自【微积分】思想中的“无穷”、“极限”,“先微分后积分”的观点。或者说傅里叶级数/变换是微积分思想应用在信号领域的实例化和拓展。
铺垫:微积分发展背后的逻辑思想
你也能懂的微积分 - 知乎 (zhihu.com)
古希腊人和古代中国人都知道用已知的多边形去逼近复杂曲线图形,阿基米德用穷竭法算出了一些简单曲线围成的面积,刘微用正多边形去逼近圆,也就是用割圆术去计算圆周率。 牛顿和莱布尼茨发现了“微分和积分是一对互逆运算”这个惊天大秘密,正式宣告了微积分的诞生。 柯西和魏尔斯特拉斯用ε-δ语言重新定义了极限,把风雨飘摇中的微积分重新建立在坚实的极限理论基础之上,彻底解决了幽灵般的无穷小量的问题,解决了第二次数学危机,也在数学领域解决了芝诺悖论。 勒贝格基于集合论,对积分理论进行了一次革命,建立了定义范围更广的勒贝格积分,并且进一步把这场革命推进到了实分析。
我把上述链接文章的结语摘录出来,既是对该文章内容的一个总结,也是为了阐述了微积分几千年的发展脉络和内在逻辑——“无穷”、“极限”,“先微分后积分”。
有了这一点的铺垫,结合下述几篇文章就不难理解“各种不同的信号怎么就能统一地这种无穷的函数组合形式来表达”这一疑问了。
傅里叶级数/变换公式背后的“微分”与“积分”
傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎 (zhihu.com)
这篇文章可以说是目前看到的科普傅里叶级数/变换的一篇神作了,从点赞量可见一斑。
重点摘录如下内容:矩形波的分解——傅里叶级数的直观理解
如果我说我能用前面说的正弦曲线波叠加出一个带90度角的矩形波来,你会相信吗?你不会,就像当年的我一样。但是看看下图:
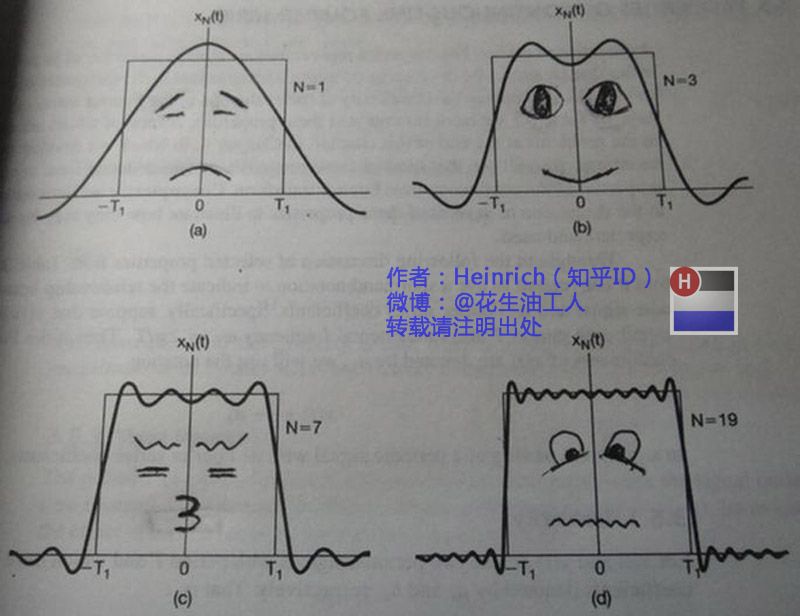
添加图片注释,不超过 140 字(可选)
第一幅图是一个郁闷的正弦波cos(x) 第二幅图是2个卖萌的正弦波的叠加cos(x)+a.cos(3x) 第三幅图是4个发春的正弦波的叠加 第四幅图是10个便秘的正弦波的叠加 随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,大家从中体会到了什么道理? (只要努力,弯的都能掰直!) 随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准90度角的矩形波呢?不幸的告诉大家,答案是无穷多个。(上帝:我能让你们猜着我?) 不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。 还是上图的正弦波累加成矩形波,我们换一个角度来看看:
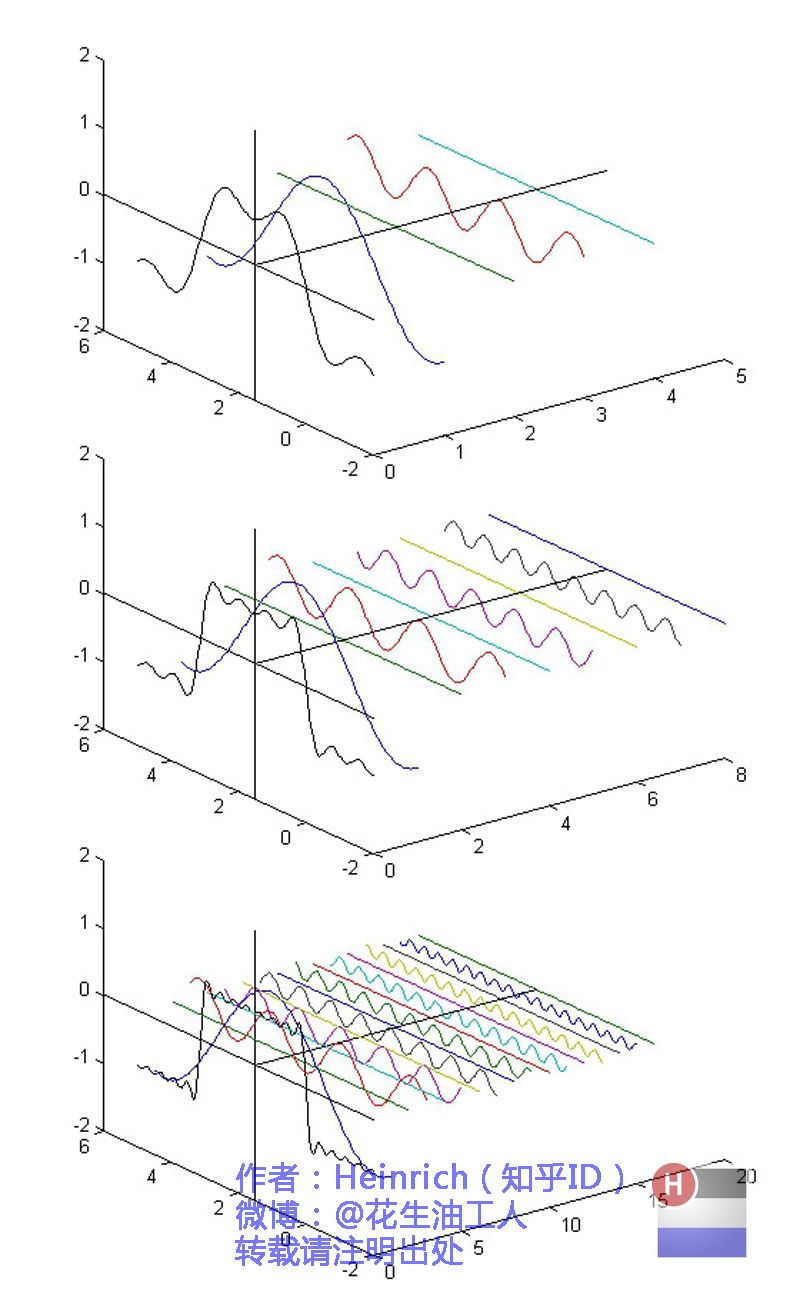
在这几幅图中,最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。一定有细心的读者发现了,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为0的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。 这里,不同频率的正弦波我们成为频率分量。 好了,关键的地方来了!! 如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元。 对于我们最常见的有理数轴,数字“1”就是有理数轴的基本单元。 时域的基本单元就是“1秒”,如果我们将一个角频率为的正弦波cos(t)看作基础,那么频域的基本单元就是。 有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
千言万语,总结一下就是,傅里叶级数/变换运用了与微积分相同的思想方法,那就是选取一个特殊的基本单元,通过无限的组合来构成普遍的一般的频域信号。
其背后的道道是不是很眼熟?
说白了还是微积分那一套“无穷”、“极限”,“先微分后积分”。
如果上述文章还是有点抽象,可以搭配以下文章作为辅食
傅里叶级数与傅里叶变换 - 知乎 (zhihu.com)
相关内容如下:
如下图所示,在笛卡尔坐标系中,由于我们定义了一组基 ,因此坐标系中的所有点才能够被一个坐标唯一地表示:
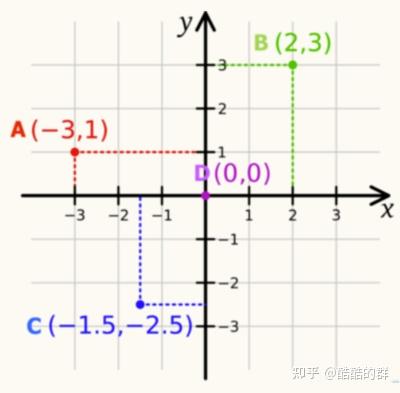
添加图片注释,不超过 140 字(可选)
这样的好处是有了坐标以后,点与点之间就不再是相互孤立的存在,也就有了距离的关系。这个过程就是一种变换,即把坐标变换到坐标系中。 这种简单的变换是将空间中的点使用一组基来表示,点是基的加权累加,而类比到函数中,对于一个函数,我们期待使用一组基函数来表示。傅里叶级数与傅里叶变换就是用来办到这件事的方法,其中傅里叶级数能够将任意周期函数表示成一组基函数依照各自的系数的累加,而傅里叶变换针对的是非周期函数。 首先阐述傅里叶级数,它可以将任意周期函数分解为简单震荡函数(正弦函数和余弦函数,这些函数作为基函数)的加和。具体地,对于周期为 的周期函数 ,可以分解为三角函数的组合: 这里的 ,称为基频率。类比笛卡尔坐标系, 就相当于坐标,而 就相当于基向量,不同的是, 是一组函数,而基向量是一组向量,笛卡尔坐标系使用基向量来表示点,傅里叶级数使用基函数来表示周期函数。
讲明白了傅里叶级数/变换公式形式的背后逻辑之后,就可以来说说第二个问题了,为什么傅里叶级数/变换的基本函数单元是正余弦函数了。
傅里叶级数/变换的正余弦函数——天命所归
还是那一套,放文章,讲道理
为什么要进行傅立叶变换? (qq.com)
一言以蔽之:
为什么我们要用正弦曲线来代替原来的曲线呢?如我们也还可以用方波或三角波来代替呀,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
好像过于结论性,想看看详细的,严密的论述过程?
有!
如何理解傅立叶级数、傅立叶变换公式? (qq.com)
摘取部分内容:以一个简单的信号函数为例,说明为何要用正余弦函数的组合作为基本的函数单元。
假设 是周期为 的函数,傅里叶男爵会怎么构造三角函数的和,使之等于 ? 2.1 常数项 对于 这样的常数函数:
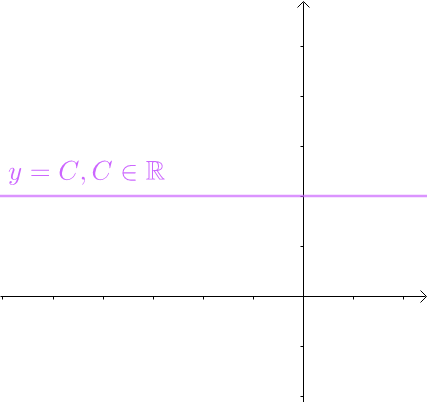
根据周期函数的定义,常数函数是周期函数,周期为任意实数。 所以,分解里面得有一个常数项。 2.2 通过 进行分解 首先, 是周期函数,进行合理的加减组合,结果可以是周期函数。 其次,它们的微分和积分都很简单。 然后, 是奇函数,即: 从图像上也可以看出, 关于原点对称,是奇函数:
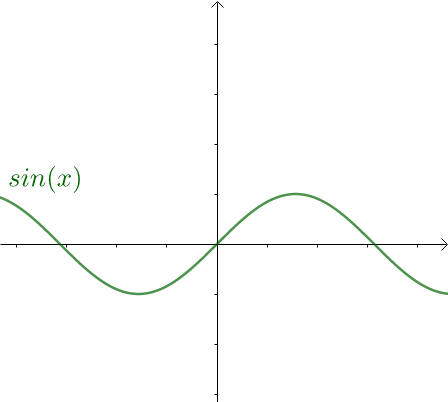
添加图片注释,不超过 140 字(可选)
而奇函数与奇函数加减只能得到奇函数,即: 其中, 表示奇函数。 而 是偶函数,即: 从图像上也可以看出, 关于 轴对称,是偶函数:
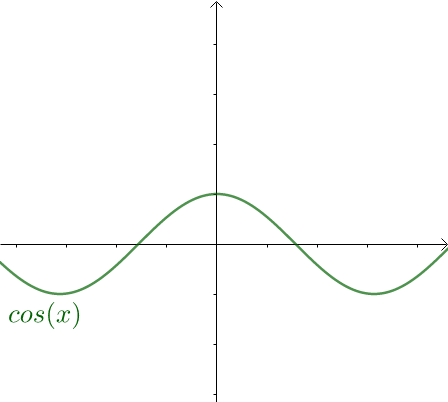
添加图片注释,不超过 140 字(可选)
同样的,偶函数与偶函数加减只能得到偶函数,即: 其中, 表示偶函数。 但是任意函数可以分解和奇偶函数之和:
![]()
添加图片注释,不超过 140 字(可选)
所以同时需要 。 2.3 保证组合出来周期为 之前说了, 是周期为 的函数,我们怎么保证组合出来的函数周期依然为 呢? 比如下面这个函数的周期为 :
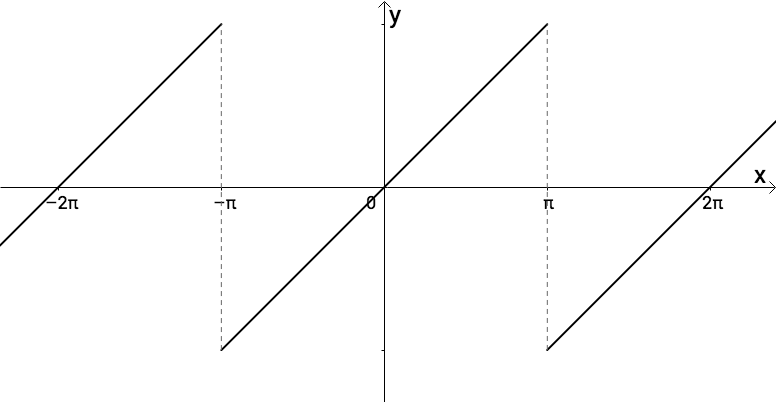
添加图片注释,不超过 140 字(可选)
很显然, 的周期也是 :
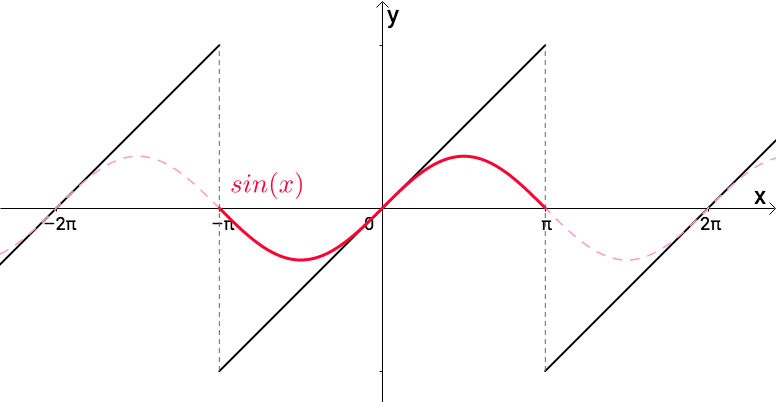
添加图片注释,不超过 140 字(可选)
的周期也是 ,虽然最小周期是 :
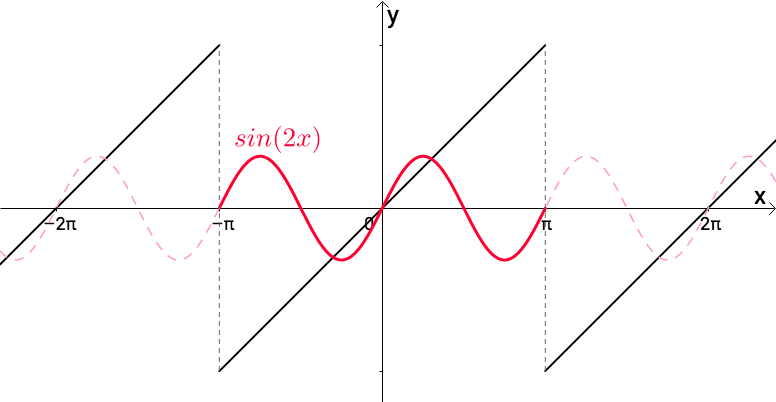
添加图片注释,不超过 140 字(可选)
很显然, 的周期都是 :
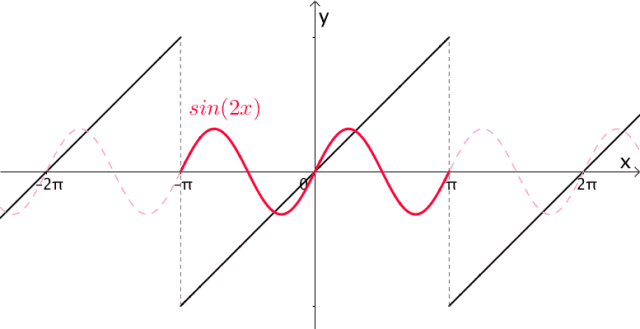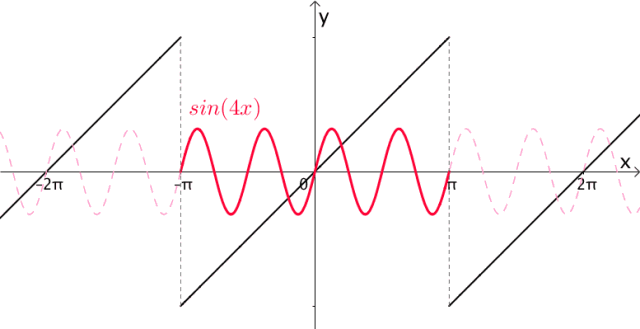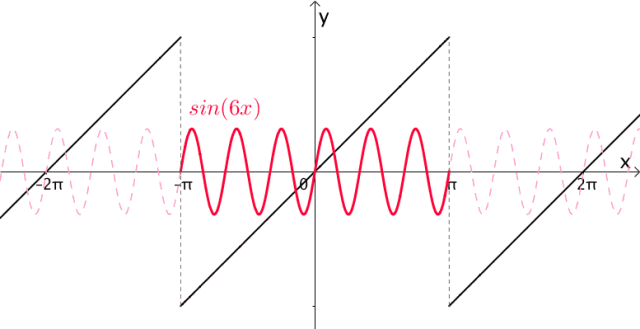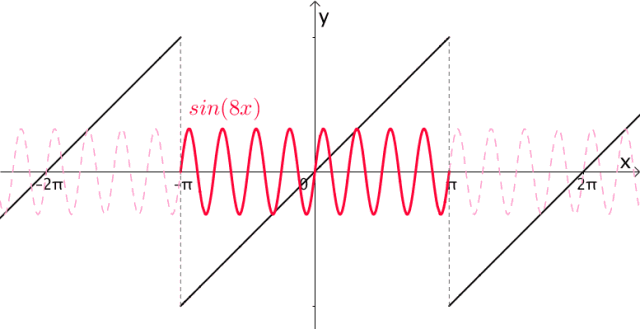
添加图片注释,不超过 140 字(可选)
更一般的,如果 的周期为 ,那么: 这些函数的周期都为 。 将这些函数进行加减,就保证了得到的函数的周期也为 。 2.4 调整振幅 现在我们有一堆周期为 的函数了,比如说
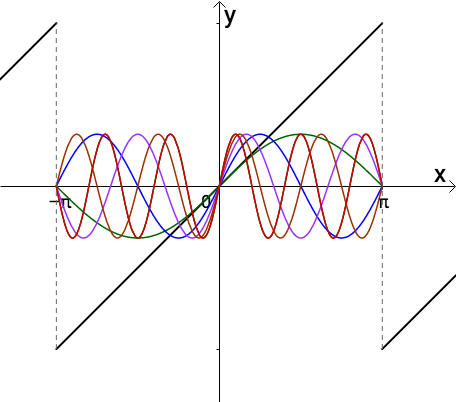
添加图片注释,不超过 140 字(可选)
通过调整振幅可以让它们慢慢接近目标函数,比如 看起来处处都比目标函数低一些:
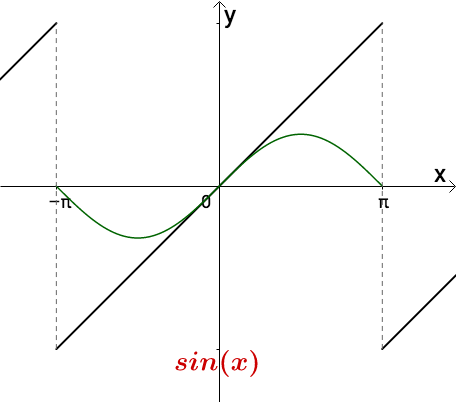
添加图片注释,不超过 140 字(可选)
把它的振幅增加一倍:
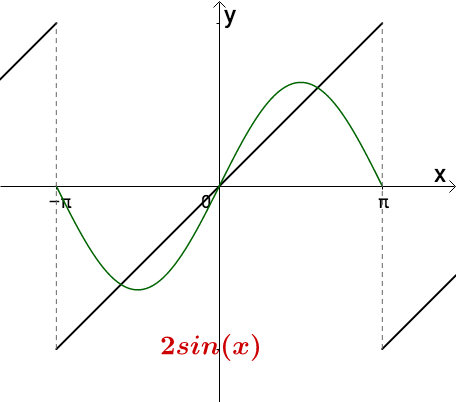
添加图片注释,不超过 140 字(可选)
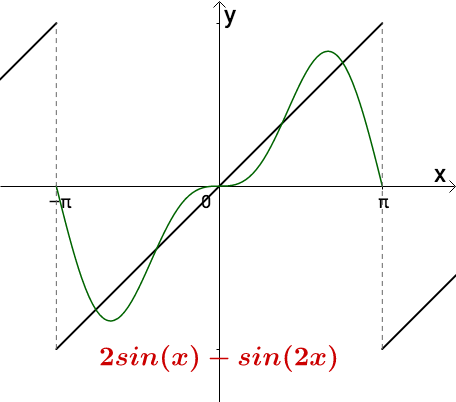
有的地方超出去了,从周期为 的函数中选择一个,减去一点:
添加图片注释,不超过 140 字(可选)
调整振幅,加加减减,我们可以慢慢接近目标函数:
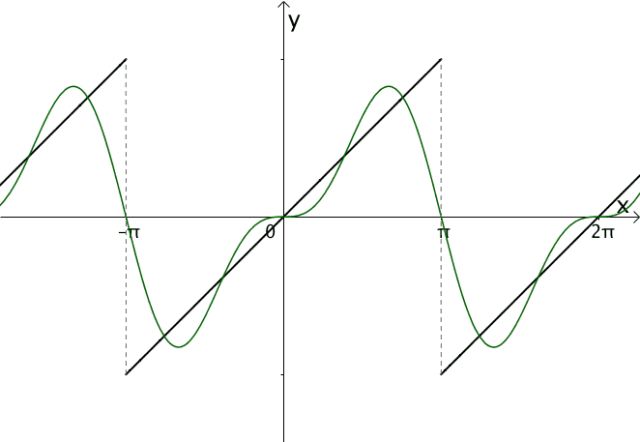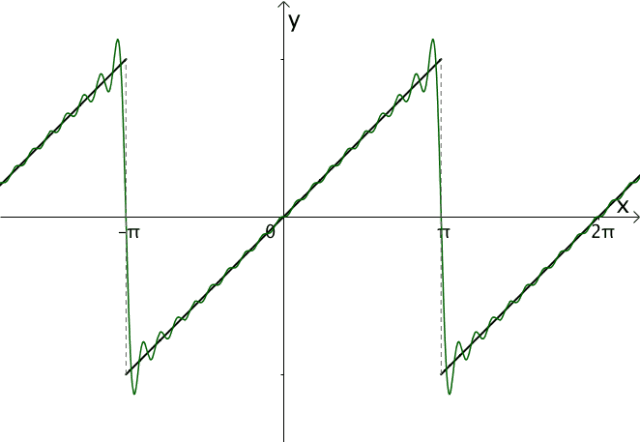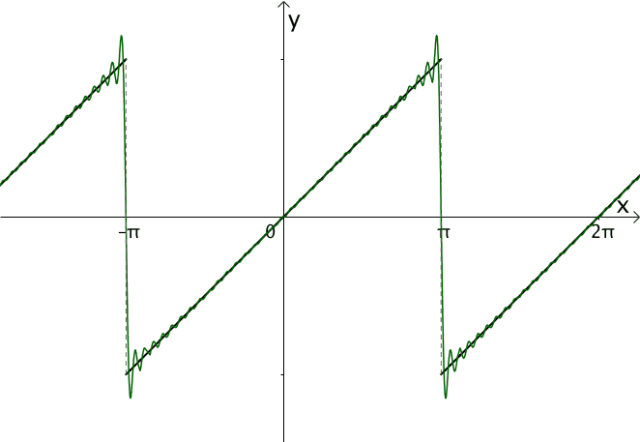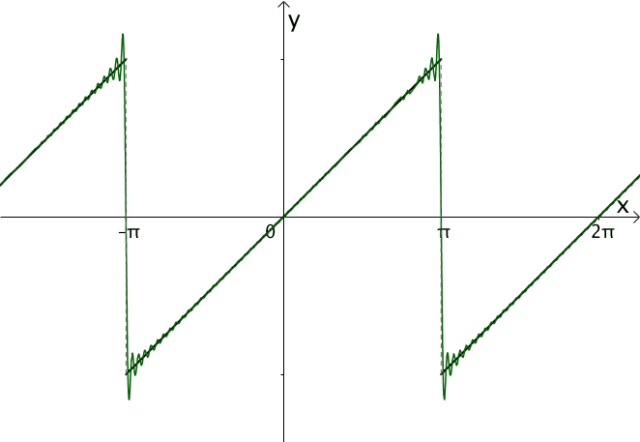
2.5 小结 综上,构造出来的三角函数之和大概类似下面的样子: 这样就符合之前的分析: -有常数项 -奇函数和偶函数可以组合出任意函数 -周期为 -调整振幅,逼近原函数
洋洋洒洒,四处搬运了不少佳作,重点都是为了说明傅里叶级数/变换背后的本质逻辑,即微积分思想的具体表现。
区别于读书时代的微积分学习重点是面向考试的解题技巧训练,考完试了也就还给老师了,毕业后从事算法方向的工作的经历,愈发认识到各类算法底层的数学原理的重要性。
如同文章开篇傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎 (zhihu.com)所说的那样:
傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。
细思,然也!
参考
*以文章中先后出现顺序为准
你也能懂的微积分 - 知乎 (zhihu.com)
傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎 (zhihu.com)
傅里叶级数与傅里叶变换 - 知乎 (zhihu.com)
为什么要进行傅立叶变换? (qq.com)
函数)
![传输层协议[精选]](http://pic.xiahunao.cn/传输层协议[精选])





)



)




)


