【513】找树左下角的值
【112】路径总和
【106】从中序与后序遍历序列构造二叉树

1.【513】找树左下角的值

1.1题目描述

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

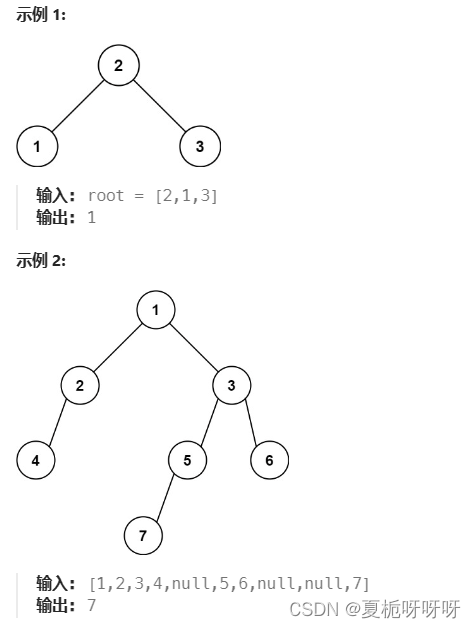
提示:

• 二叉树的节点个数的范围是 [1,10⁴]
• -2³¹ <= Node.val <= 2³¹ - 1

1.2 解题思路

1.2.1 迭代法思路

本题要找出树的最后一行的最左边的值，使用层序遍历是非常简单的，只需要记录最后一行第一个节点的数值就可以了。

1.2.2 递归法思路

题目：在树的最后一行找到最左边的值。

首先要是最后一行，然后是最左边的值。

如果使用递归法，如何判断是最后一行呢？其实就是深度最大的叶子节点一定是最后一行。所以要找深度最大的叶子节点。

那么如何找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 根节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。

递归三部曲

• 1. 确定递归函数的参数和返回值

参数必须有要遍历的树的根节点，还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了，所以递归函数的返回类型为void。

本题还需要类里的两个全局变量，maxDepth用来记录最大深度，result记录最大深度最左节点的数值。

	int result;// 全局变量 记录最大深度int maxDepth=-1;// 全局变量 最大深度最左节点的数值public void traversal(TreeNode root,int depth)

• 2. 确定终止条件

当遇到叶子节点的时候，就需要统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度。

		if (root.left==null && root.right==null){if (depth>maxDepth){maxDepth=depth;// 更新最大深度result=root.val;// 最大深度最左面的数值}return;}

• 3. 确定单层递归的逻辑

在找最大深度的时候，递归的过程中依然要使用回溯

		if (root.left!=null){//左depth++;traversal(root.left,depth);//回溯depth--;}if (root.right!=null){//右depth++;traversal(root.right,depth);//回溯depth--;}return;

1.3 java代码实现

1.3.1 迭代法java代码实现

class Solution {public int findBottomLeftValue(TreeNode root) {//迭代法  层次遍历Queue<TreeNode> que=new LinkedList<>();que.offer(root);int res=0;while (!que.isEmpty()){int len=que.size();for (int i = 0; i < len; i++) {TreeNode tempNode=que.poll();// 记录最后一行第一个元素if (i==0){res=tempNode.val;}if (tempNode.left!=null){que.offer(tempNode.left);}if (tempNode.right!=null){que.offer(tempNode.right);}}}return res;}
}

1.3.2 递归法java代码实现

class Solution {int result;// 全局变量 记录最大深度int maxDepth=-1;// 全局变量 最大深度最左节点的数值public int findBottomLeftValue(TreeNode root) {//递归traversal(root,0);return result;}public void traversal(TreeNode root,int depth){if (root.left==null && root.right==null){if (depth>maxDepth){maxDepth=depth;// 更新最大深度result=root.val;// 最大深度最左面的数值}return;}if (root.left!=null){//左depth++;traversal(root.left,depth);//回溯depth--;}if (root.right!=null){//右depth++;traversal(root.right,depth);//回溯depth--;}return;}
}

递归函数简写：

public void traversal(TreeNode root,int depth){if (root.left==null && root.right==null){if (depth>maxDepth){maxDepth=depth;// 更新最大深度result=root.val;// 最大深度最左面的数值}return;}if (root.left!=null){//左traversal(root.left,depth+1);// 隐藏着回溯}if (root.right!=null){//右traversal(root.right,depth+1);// 隐藏着回溯}return;}

2. 【112】路径总和

2.1题目描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

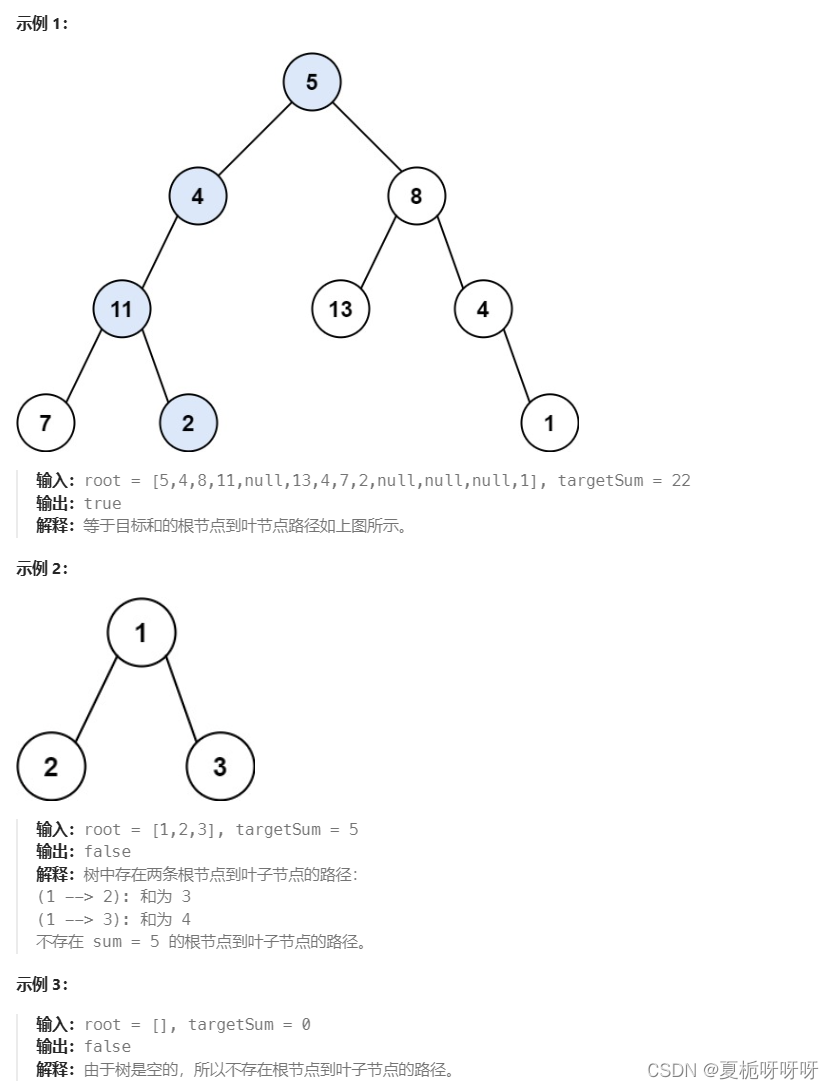
提示：

• 树中节点的数目在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

2.2 解题思路

本题可以采用深度遍历的方式来遍历（本题前中后序都可以，无所谓，因为根节点也没有处理逻辑）。，递归法

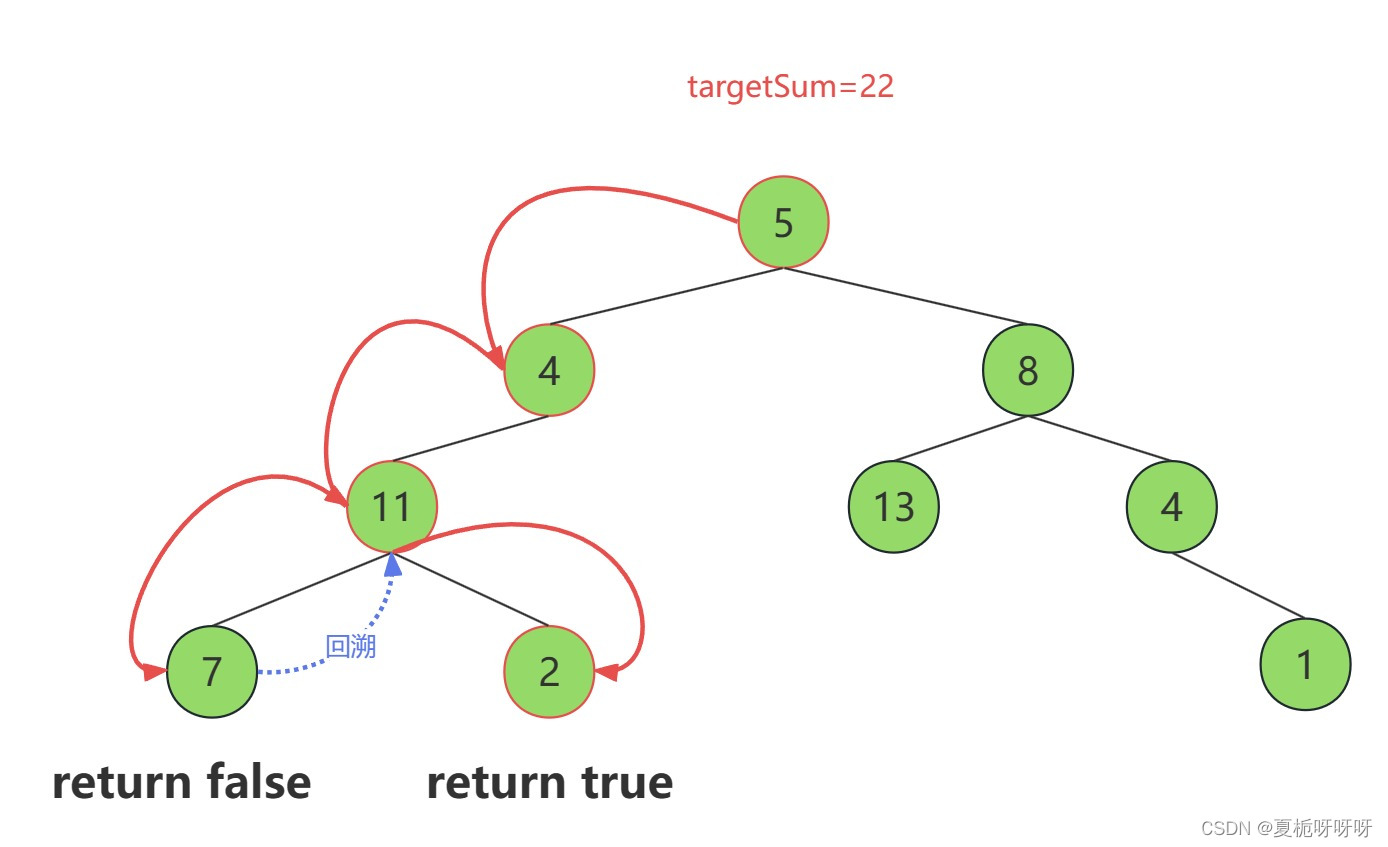
2.3 java代码实现

class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if (root==null){return false;}targetSum -= root.val;//叶子结点if (root.left==null && root.right==null){return targetSum==0;}if (root.left!=null){boolean left=hasPathSum(root.left,targetSum);//已经找到if (left){return true;}}if (root.right!=null){boolean right=hasPathSum(root.right,targetSum);//已经找到if (right){return true;}}return false;}
}

3.【106】从中序与后序遍历序列构造二叉树

3.1题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

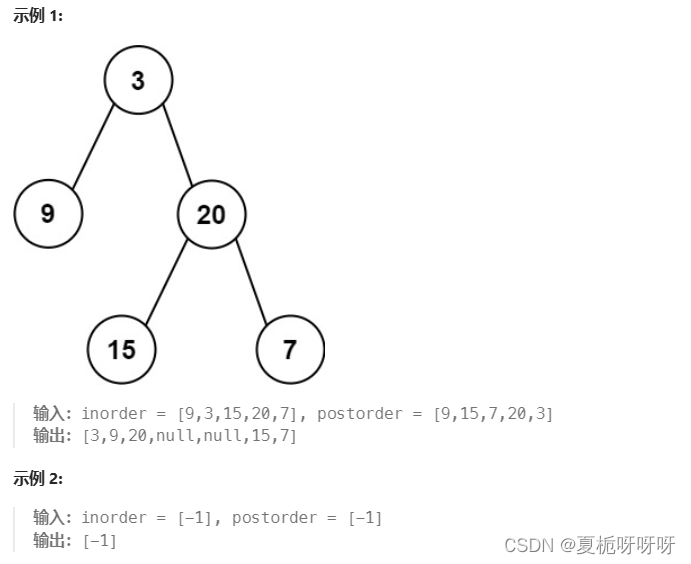
提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

3.2 解题思路

中序遍历与后序遍历构造二叉树的理论知识

以 后续数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后续数组。一层一层的切下去，每次后续数组的最后一个元素就是节点元素。

流程如下：

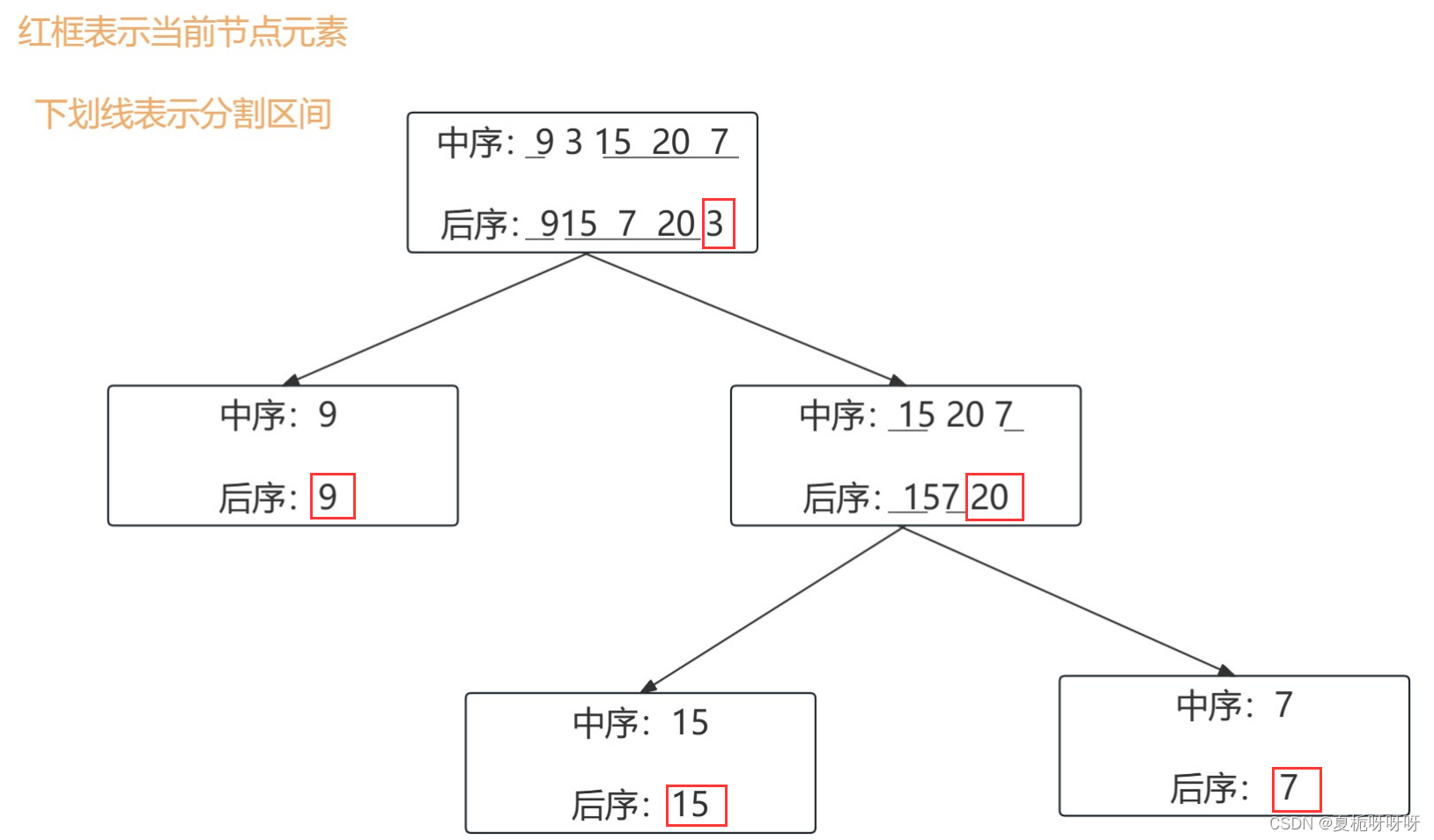
代码该怎样写呢？提到一层一层切割，就应该想到了递归

• 1. 如果数组大小为0的话，说明是空节点了
• 2. 如果不为空，那么取后序数组的最后一个元素作为节点元素
• 3. 找到后序数组最后一个元素在中序数组中的位置，作为切割点
• 4. 切割中序数组，切成中序左数组和中序右数组（顺序一定不能弄反了，一定要先切中序数组）
• 5. 切割后序数组，切成后序左数组和后序右数组
• 6. 递归处理左区间和右区间

3.3 java代码实现

class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {if (postorder.length==0 || inorder.length==0){return null;}return buildHelper(inorder,0,inorder.length,postorder,0, postorder.length);}public TreeNode buildHelper(int[] inorder,int inorderBegin,int inorderEnd,int[] postorder,int postBegin,int postEnd){if (postBegin==postEnd){return null;}//根节点int rootVal=postorder[postEnd-1];TreeNode root=new TreeNode(rootVal);//切割点int middleIndex;for (middleIndex=inorderBegin;middleIndex<inorderEnd;middleIndex++){if (inorder[middleIndex]==rootVal){break;}}//切割中序数组//左中序数组，左闭右开[leftInorderBegin,leftInoderEnd)int leftInorderBegin=inorderBegin;int leftInoderEnd=middleIndex;//右中序数组，左闭右开[rightInorderBegin,leftInoderEnd)int rightInorderBegin=middleIndex+1;int rightInoderEnd=inorderEnd;//切割后序数组//左后序数组，左闭右开[leftPostorderBegin,leftPostoderEnd)int leftPostorderBegin=postBegin;//终止位置是 需要加上 中序区间的大小sizeint leftPostoderEnd=postBegin+(middleIndex-inorderBegin);//右后序数组，左闭右开[rightPostorderBegin,leftPostoderEnd)int rightPostorderBegin=leftPostoderEnd;int rightPostoderEnd=postEnd-1;//排除最后一个元素，已经作为节点了root.left=buildHelper(inorder,leftInorderBegin,leftInoderEnd,postorder,leftPostorderBegin,leftPostoderEnd);root.right=buildHelper(inorder,rightInorderBegin,rightInoderEnd,postorder,leftPostorderBegin,rightPostoderEnd);return root;}
}

class Solution {Map<Integer,Integer> map;//方便根据数值查找位置public TreeNode buildTree(int[] inorder, int[] postorder) {map=new HashMap<>();// 用map保存中序序列的数值对应位置for (int i=0;i<inorder.length;i++){map.put(inorder[i],i );}return findNode(inorder,0,inorder.length,postorder,0,postorder.length);}public TreeNode findNode(int[] inorder,int inorderBegin,int inorderEnd,int[] postorder,int postBegin,int postEnd){//参数里的范围都是左闭右开if (inorderBegin>=inorderEnd || postBegin>=postEnd){return null;}// 找到后序遍历的最后一个元素在中序遍历中的位置int rootIndex=map.get(postorder[postEnd-1]);TreeNode root=new TreeNode(inorder[rootIndex]);//构造节点//保存中序左子树个数，用来确定后序数列的个数int lenOfleft=rootIndex-inorderBegin;root.left=findNode(inorder,inorderBegin,rootIndex,postorder,postBegin,postBegin+lenOfleft);root.right=findNode(inorder,rootIndex+1,inorderEnd,postorder,postBegin+lenOfleft,postEnd-1);return root;}}