- 一、导入数据处理
- 二、核心——边缘分析
- 三、聚类分析
- 四、网络密度
一、导入数据处理
将数据导入Ucinet首先需要对数据进行处理。
承接上一期的数据格式:【社会网络分析第5期】gephi使用指南
原先得到的数据格式如下:
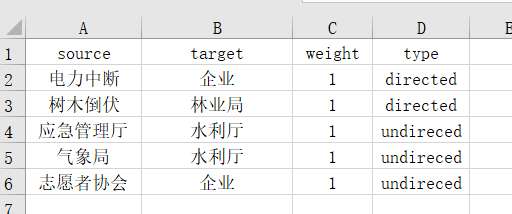
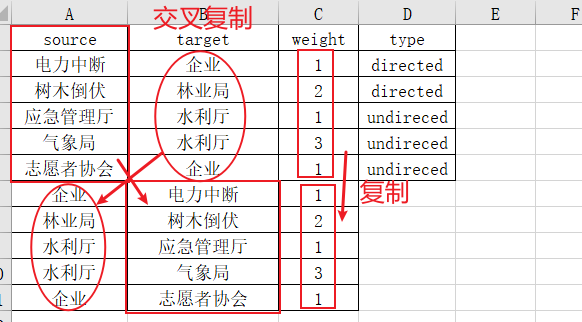
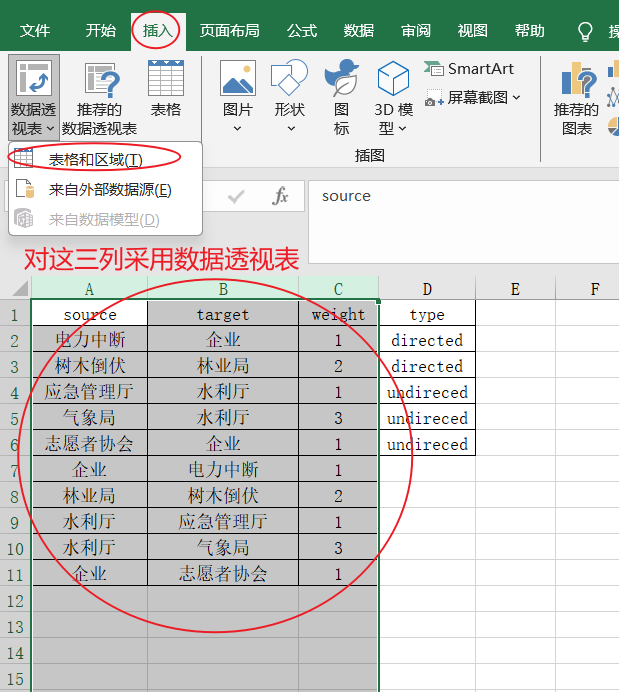


接下来打开ucinet:
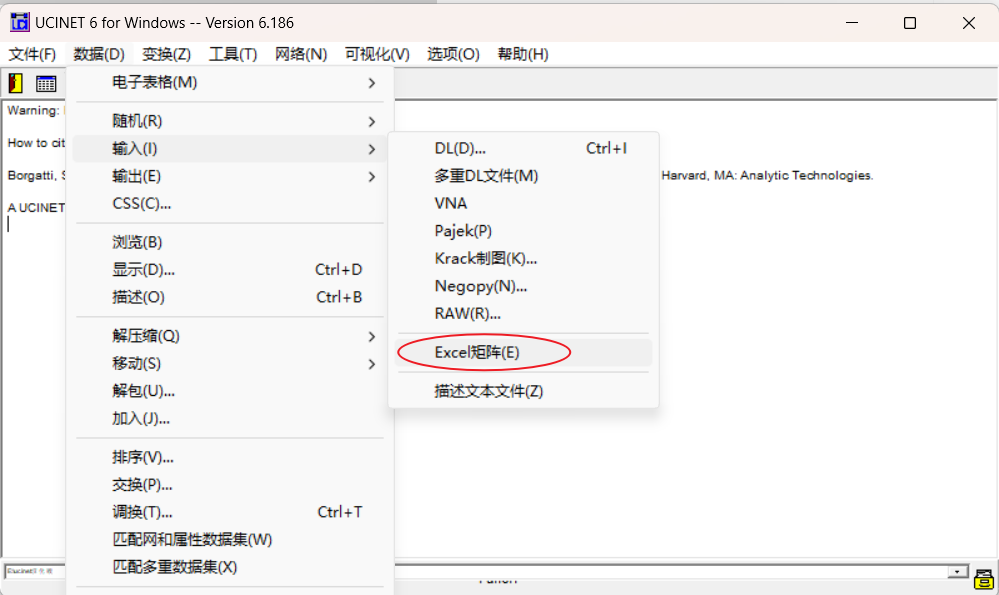
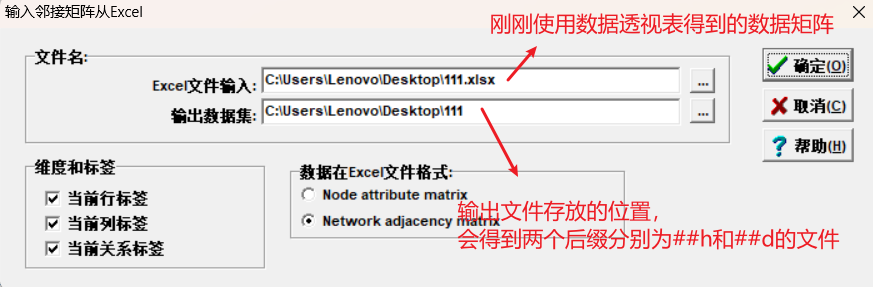
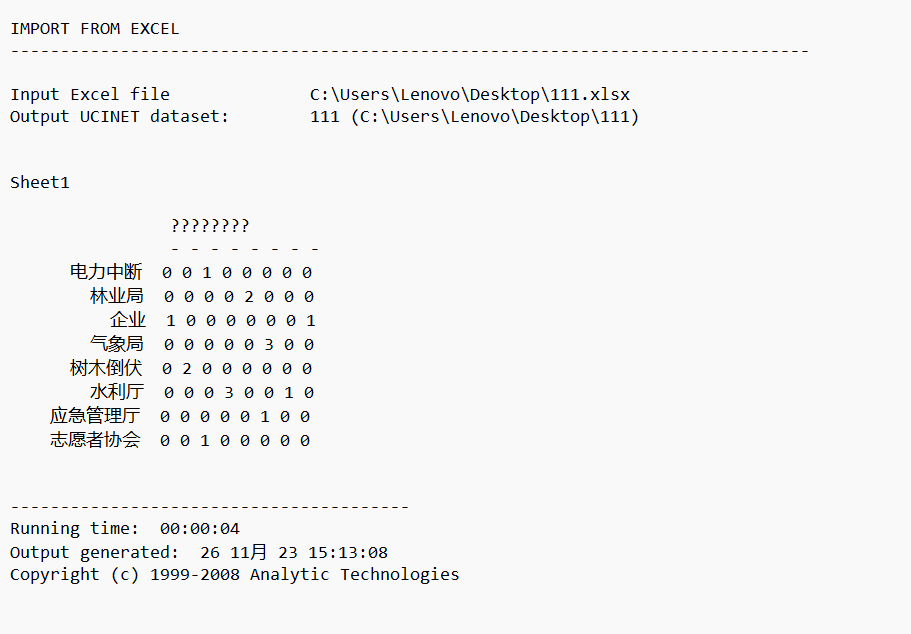

之后我们就可以使用输出的数据去进行其他的分析运算了。
二、核心——边缘分析
例如,接下来我们要对网络进行核心——边缘分析:
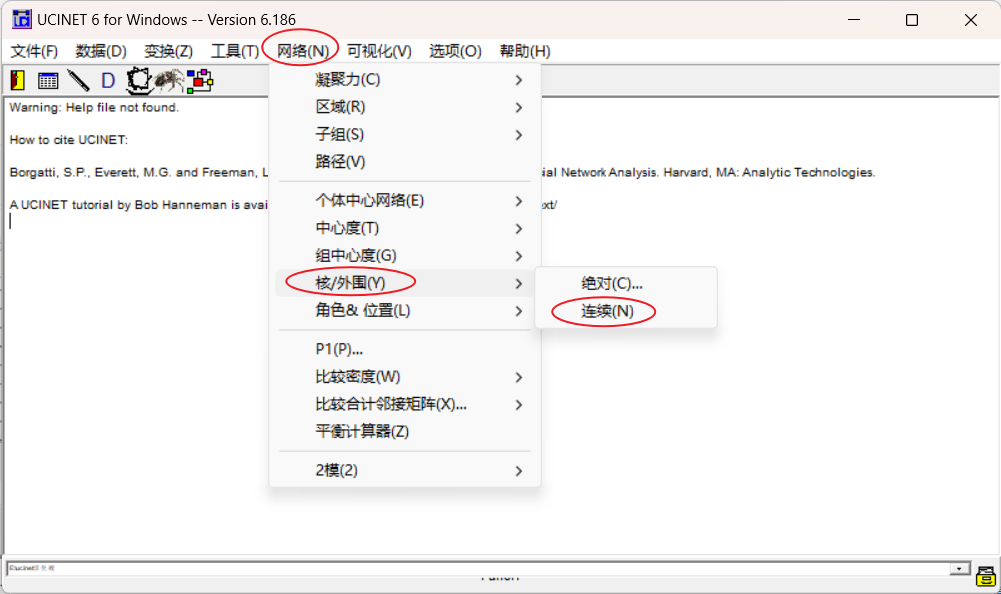
这里选择连续是因为数值型数据是连续型的。
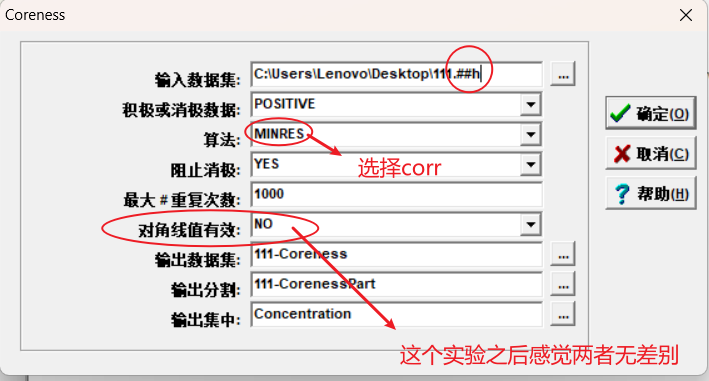
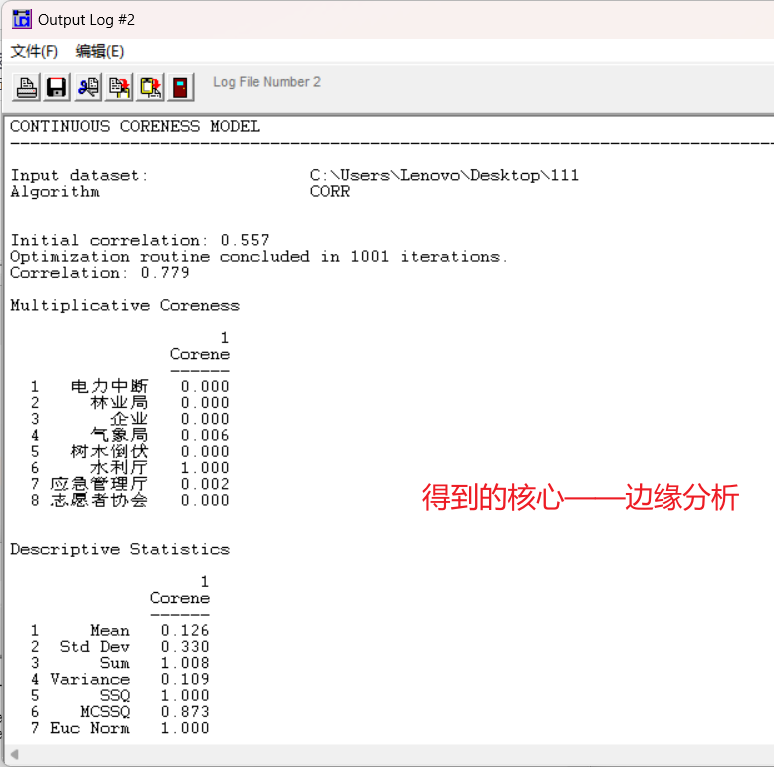
由于输出的是文本格式,因此需要自己使用excel的函数或者数据分列进行处理。
关于核心——边缘,如何区分哪些是核心节点,哪些是边缘节点?
- 可以把最大值的节点当成核心节点,之后以一个数值作为分界线,例如:小于0.05的都是边缘节点,在最高值和0.05之间的节点都称作半核心节点。
三、聚类分析
聚类分析如下:
之后还是导入后缀为##h的文件
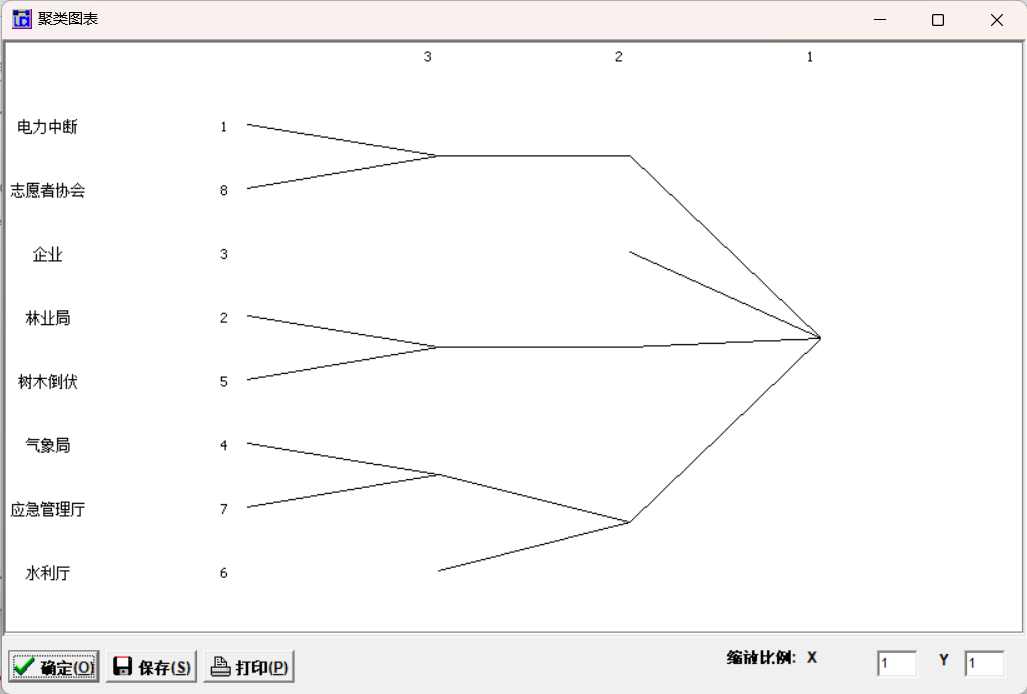
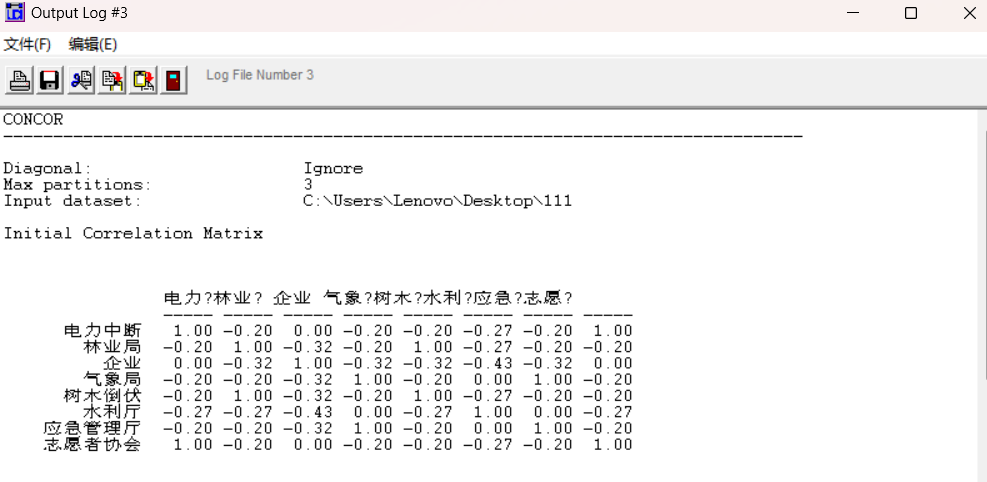

- 比如第二个模块和第三个模块之间联系的紧密程度。
四、网络密度
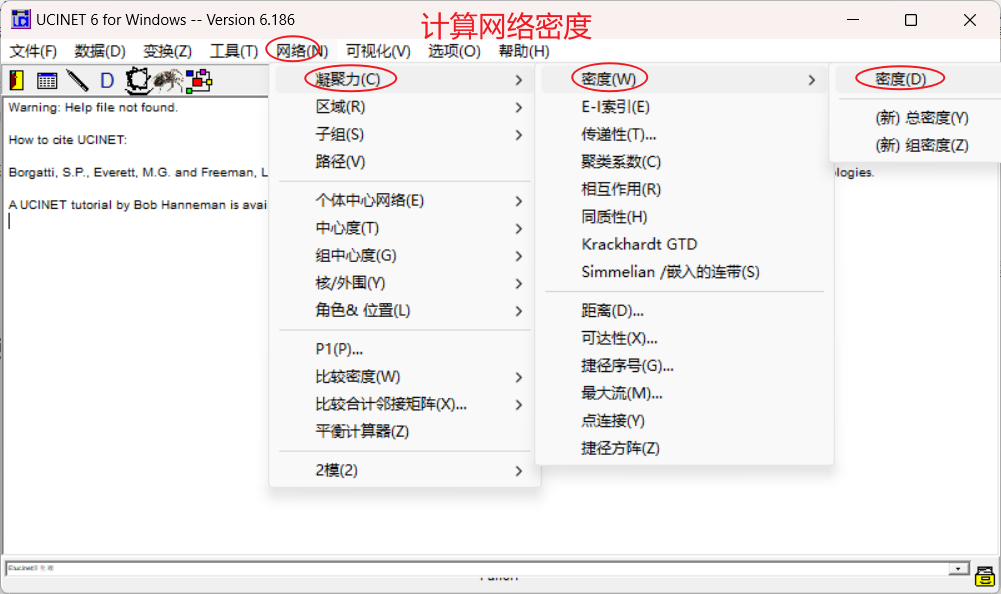
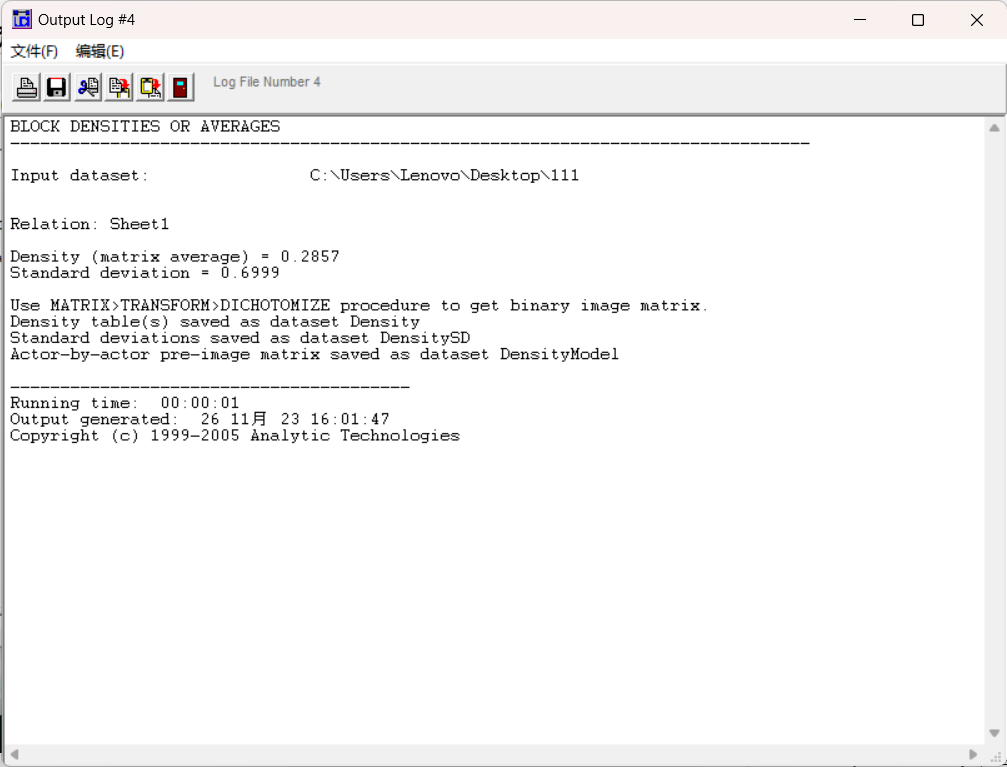
计算得到网络密度是0.28
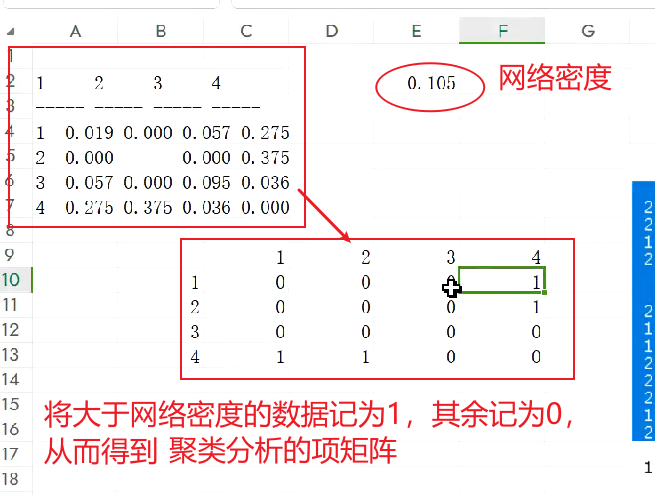
这个项矩阵能够体现这两个模块内部的联系是否相较于整个图会更加紧密。










)

)

)


: Blob Analysis 自主练习)

