1.对象数组中，对象中有对象，数组根据对象中的对象打平
[{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '固定收益类',rowName2: '交易类',rowName3: '次级'},{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '固定收益类',rowName2: '交易类',rowName3: '中期'},{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '权益类',rowName2: '',rowName3: 'A股'},{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '权益类',rowName2: '',rowName3: '港股'}
]
[{ '68443': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '次级' },{ '68457': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '次级' },{ '68443': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '中期' },{ '68457': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '中期' },{ '68443': 0, rowName1: '权益类', rowName2: '', rowName3: 'A股' },{ '68457': 0, rowName1: '权益类', rowName2: '', rowName3: 'A股' },{ '68443': 0, rowName1: '权益类', rowName2: '', rowName3: '港股' },{ '68457': 0, rowName1: '权益类', rowName2: '', rowName3: '港股' }
]方法：使用JavaScript的数组方法 .reduce() 来解决这个问题。.reduce() 方法在数组中的每个元素上执行一个reducer函数，并返回一个单一的输出值。
这段代码首先将原始数组array中的每一项curr中的indexValueMap的键值对作为对象推入累积器数组acc中。然后将每一项的其他属性rowName1, rowName2, rowName3添加到这个对象中。最后返回累积器数组，得到的结果就是你希望得到的形式。
let array = [ // ...你的原始数组
]; let result = array.reduce((acc, curr) => { for (let key in curr.indexValueMap) { acc.push({ [key]: curr.indexValueMap[key], rowName1: curr.rowName1, rowName2: curr.rowName2, rowName3: curr.rowName3, }); } return acc;
}, []); console.log(result);function flattenArray(arr: any) {let result: any = [];arr.forEach((obj: any) => {let indexValueMap = obj.indexValueMap;let newObj = { ...obj }delete newObj.indexValueMaplet newArr = []for (let key in indexValueMap) {let tempObj = JSON.parse(JSON.stringify(newObj))tempObj[key] = indexValueMap[key]newArr.push(tempObj)}result.push(newArr)})result = result.flat(1)return result;
}2.树形结构数组，其中层级不一定，获取数组中最大的层级
这个问题的解决需要一个深度优先遍历（DFS）的算法。
getMaxLevel函数会遍历给定的数据数组，并使用深度优先搜索找出最大的层级。它在遍历每个节点时都会检查是否存在children属性，如果存在，则层级加一，并对每个子节点进行同样的处理。在遍历过程中，它会持续更新最大的层级数。最后，它会返回最大的层级数。
需要注意的是，这个函数假设给定的数据数组的结构是一致的，即每个对象都有labelName、children和indexValueMap属性，且children是一个对象数组。如果数据结构可能有所不同，你可能需要添加一些错误处理代码。
function getMaxLevel(data) { let maxLevel = 0; function dfs(node, level) { if (node.children) { level++; for (let child of node.children) { dfs(child, level); } } maxLevel = Math.max(maxLevel, level); } for (let item of data) { dfs(item, 0); } return maxLevel;
} let data = [/* Your data */];
console.log(getMaxLevel(data));3.对象数组中，去除key值包含某个字符串的元素
let flatArr = getFlattenArr(arr, 'indexMap')//根据indexValueMao展开表格前去掉多余数据
function getFlattenArr(arr: any, delKey: any) {arr.map((obj: any) => {const keys = Object.keys(obj);keys.forEach((k) => {if (k.startsWith(delKey)) {delete obj[k]}})return obj});return arr
}4.通过两个栈实现一个队列
栈和队列是两种常见的数据结构。栈遵循 LIFO（后进先出）原则，而队列遵循 FIFO（先进先出）原则。可以通过两个栈来实现一个队列。
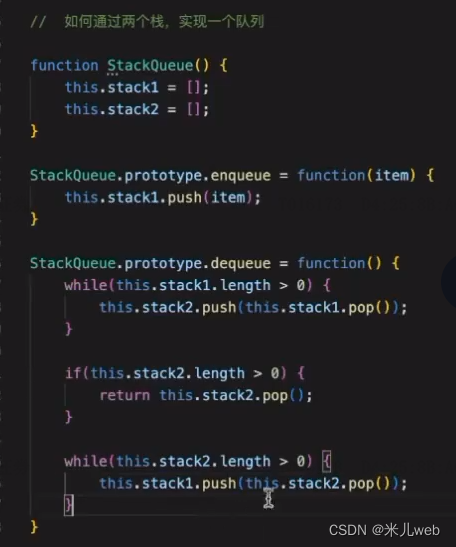
class Queue { constructor() { this.stack1 = []; this.stack2 = []; } enqueue(element) { this.stack1.push(element); } dequeue() { if (this.stack2.length === 0) { while (this.stack1.length > 0) { this.stack2.push(this.stack1.pop()); } } return this.stack2.pop(); }
}while() 是一个函数，而不是一个语句。它用于在满足某个条件的情况下反复执行代码块。
while() 函数的语法如下：
while (condition) { // code to be executed while the condition is true
}在这个语法中，condition 是一个表达式，它会在每次循环迭代之前进行评估。如果 condition 的值为 true，则执行循环体内的代码；否则，循环会终止。
5.二叉树中，有三种常见的遍历方式：前序遍历、中序遍历和后序遍历。
- 前序遍历 (Preorder Traversal)
在前序遍历中，首先访问根节点，然后递归地访问左子树，最后访问右子树。
function preorderTraversal(root) { const result = []; function helper(node) { if (node === null) return; result.push(node.value); // 访问根节点 helper(node.left); // 递归访问左子树 helper(node.right); // 递归访问右子树 } helper(root); return result;
}- 中序遍历 (Inorder Traversal)
在中序遍历中，首先递归地访问左子树，然后访问根节点，最后递归地访问右子树。
function inorderTraversal(root) { const result = []; function helper(node) { if (node === null) return; helper(node.left); // 递归访问左子树 result.push(node.value); // 访问根节点 helper(node.right); // 递归访问右子树 } helper(root); return result;
}- 后序遍历 (Postorder Traversal)
在后序遍历中，首先递归地访问左子树，然后递归地访问右子树，最后访问根节点。
function postorderTraversal(root) { const result = []; function helper(node) { if (node === null) return; helper(node.left); // 递归访问左子树 helper(node.right); // 递归访问右子树 result.push(node.value); // 访问根节点 } helper(root); return result;
}
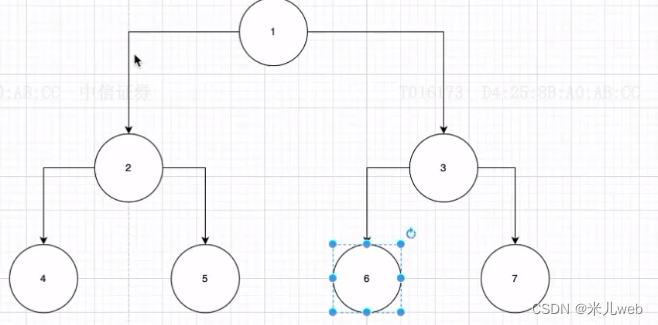
前序：1245367
中序：4251637
后序：4526731
四大算法：分治、回溯、贪心、动规
分治法是一种将问题划分为小规模子问题的算法设计策略。分治法通过将问题划分为更小的部分，然后分别解决这些子问题，最后将这些子问题的解合并以得到原始问题的解。分治法的主要步骤包括：分解、解决、合并。
一个著名的使用分治法设计的算法是快速排序。在快速排序中，我们选择一个基准元素，然后将数组划分为两个子数组：一个包含所有小于基准的元素，另一个包含所有大于或等于基准的元素。然后我们对这两个子数组递归地应用快速排序。
回溯法是一种通过探索所有可能的候选解来找出所有的解的算法。回溯算法会检查每一步决策是否正确，并“回溯”或撤销先前的决策，然后继续探索其他可能的决策。这种算法通常用于解决组合优化问题，如八皇后问题、图的着色问题、旅行商问题等。
一个典型的回溯算法的实现通常包括：一个递归函数，该函数通过调用自身来处理子问题，以及一个“剪枝”函数，该函数用于排除那些不可能是最优解的候选解。
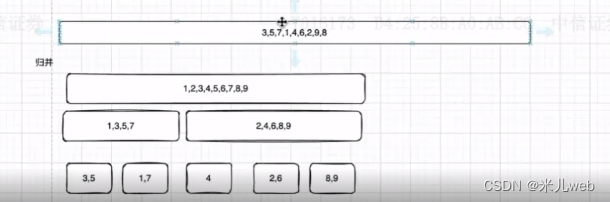
ex1:回溯法-归并排序
Math.floor() 是JavaScript的一个内置函数，用于返回小于或等于一个给定数字的最大整数。换句话说，它向下取整。
Math.floor(3.7); // 返回 3
Math.floor(3.8); // 返回 3
Math.floor(-3.7); // 返回 -4
Math.floor(-3.8); // 返回 -4
function mergeSort(arr){ if(arr.length === 1) return arrconst midIdx = Math.floor(arr.length /2) return merge(mergeSort(arr.slice(0,midIdx)), mergeSort(arr.slice(midIdx)))}// [1,3,5,7]--[2,4,6,8,9]function merge(leftArr, rightArr) {let temp = []while(leftArr.length>0 && rightArr.length>0){if(leftArr[0]<rightArr[0]){temp.push(leftArr.shift())}else{temp.push(rightArr.shift())}} return temp.concat(leftArr).concat(rightArr) }let arr = [1,8,3,9,5,4,6,2,7]console.log(mergeSort(arr)) //[1,2,3,4,5,6,7,8,9]
function mergeSort(arr) { // 如果数组只有一个元素，直接返回 if (arr.length <= 1) { return arr; } // 将数组分成两部分，分别进行递归排序 const mid = Math.floor(arr.length / 2); const left = arr.slice(0, mid); const right = arr.slice(mid); return merge(mergeSort(left), mergeSort(right));
} function merge(left, right) { // 合并两个有序数组 const result = []; let i = 0; let j = 0; while (i < left.length && j < right.length) { if (left[i] < right[j]) { result.push(left[i]); i++; } else { result.push(right[j]); j++; } } // 将剩余元素添加到结果数组中 while (i < left.length) { result.push(left[i]); i++; } while (j < right.length) { result.push(right[j]); j++; } return result;
}
