Adversarial Attack on Graph Structured Data----《图结构数据的对抗攻击》

摘要

  基于图结构的深度学习已经在各种应用中显示出令人兴奋的结果。然而，与图像或文本对抗攻击和防御的大量研究工作相比，此类模型的鲁棒性却很少受到关注。在本文中，我们重点关注通过修改数据组合结构来欺骗深度学习模型的对抗性攻击。我们首先提出一种基于强化学习的攻击方法，该方法学习可泛化的攻击策略，同时只需要来自目标分类器的预测标签。在额外的预测置信度或梯度可用的情况下，我们进一步提出基于遗传算法和梯度下降的攻击方法。我们使用合成数据和真实数据来表明，在图级和节点级分类任务中，一系列图神经网络模型很容易受到这些攻击。我们还表明此类攻击可用于诊断学习的分类器。

引言

  图结构在许多实际应用中发挥着重要作用。使用深度学习方法对结构化数据进行表示学习在各种应用中都显示出了有希望的结果，包括药物筛选、蛋白质分析、知识图补全等。
  尽管深度图网络取得了成功，但这些模型缺乏可解释性和鲁棒性，使得某些金融或安全相关应用程序面临风险。正如 Akoglu 等人分析的那样，图信息被证明在风险管理领域很重要。图敏感的评估模型通常会考虑用户与用户的关系：与许多高信用用户连接的用户也可能具有高信用。这种由深度图方法学到的启发式方法通常会产生良好的预测，但也可能会使模型面临风险。犯罪分子可能会尝试通过使用 Facebook 或 Linkedin 与其他人联系来伪装自己。这种对信用预测模型的“攻击”成本相当低，但后果可能很严重。由于每天发生大量交易，即使只有百万分之一的交易是欺诈的，欺诈者仍然可以获得巨大的利益。然而，尽管图像和文本等其他领域的对抗性攻击和防御最近取得了进展，但涉及图结构的领域却很少受到关注。
  因此，在本文中，我们重点关注一组图神经网络（GNN）模型的图对抗攻击。这是一个监督模型家族，在许多转导任务和归纳任务中取得了最先进的结果。通过节点分类和图分类问题的实验，我们将证明此类模型确实存在对抗样本。GNN 模型很容易受到此类攻击。
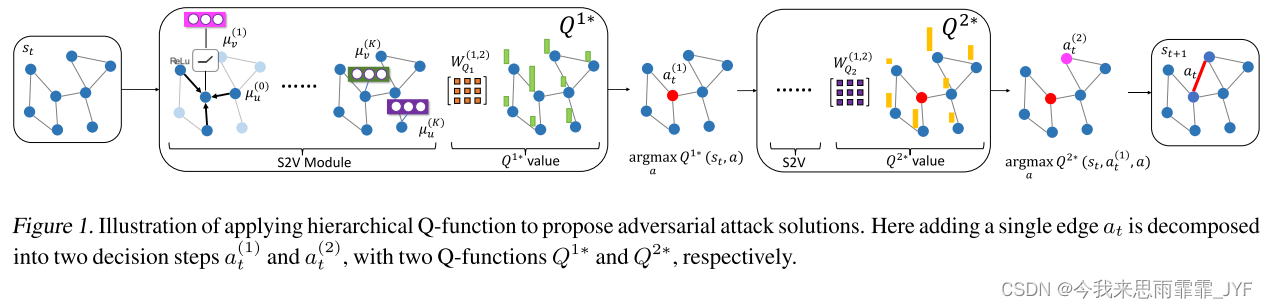
  然而，有效地攻击图结构并不是一个简单的问题。与数据是连续的图像不同，图是离散的。此外，图形结构的组合性质使其比文本困难得多。受组合优化最新进展的启发，我们提出了一种基于强化学习的攻击方法，该方法仅根据目标分类器的预测反馈来学习修改图结构。修改是通过从图中顺序添加或删除边来完成的。还使用了一种分层方法来分解二次动作空间，以使训练变得可行。图 1 说明了这种方法。我们证明，通过学习代理（黑盒）也可以提出对抗攻击的新实例，而不访问目标分类器。

  本文考虑了几种不同的对抗攻击设置。当从目标分类器中获取更多信息时（灰盒或白盒），还提出了一种基于梯度的方法和一种基于遗传算法的方法。这里我们主要关注以下三个设置：
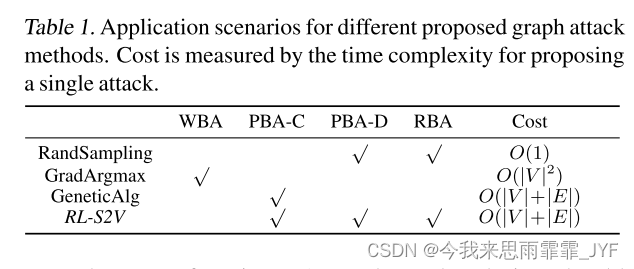
白盒攻击(WBA)：在这种情况下，攻击者可以访问目标分类器的任何信息，包括预测信息、梯度信息等。
实用黑盒攻击(PBA)：在这种情况下，只有对目标分类器的预测可用。当可以获取预测置信度时，我们将此设置表示为PBA-C；如果只允许使用离散的预测标签，我们将此设置表示为PBA-D。
限制黑盒攻击(RBA)：这种设置比PBA更进一步。在这种情况下，我们只能对部分样本进行黑盒查询，并要求攻击者对其他样本进行对抗性修改。
  我们可以看到，关于攻击者可以从目标分类器获取的信息量，我们可以将上述设置排序为WBA > PBA-C > PBA-D > RBA。为简单起见，我们关注非目标攻击，尽管它很容易扩展到目标攻击场景。

背景

  一组图用 G = { G i } i = 1 N G = \{ {G_i}\} _{i = 1}^N G={Gi​}i=1N​ 表示，其中 $\left|G\right|=N$。每个图 $G_i=(V_i,E_i)$ 由节点集 V i = { v j ( i ) } j = 1 ∣ V i ∣ {V_i} = \{ v_j^{(i)}\} _{j = 1}^{\left| {{V_i}} \right|} Vi​={vj(i)​}j=1∣Vi​∣​ 和边集 E i = { e j ( i ) } j = 1 ∣ E i ∣ {E_i} = \{ e_j^{(i)}\} _{j = 1}^{\left| {{E_i}} \right|} Ei​={ej(i)​}j=1∣Ei​∣​ 组成。在本文中，我们关注无向图，但扩展到有向图也很简单。可选地，节点或边可以具有关联的特征。本文主要研究攻击图监督分类算法。这里考虑了两种不同的监督学习设置：

归纳图分类：我们将每个图 $G_i$ 与标签 y i ∈ γ = { 1 , 2 , . . . , Y } {y_i} \in \gamma = \{ 1,2,...,Y\} yi​∈γ={1,2,...,Y} 相关联，其中 $Y$ 是类别数。数据集 $D^{(ind)}=\{(G_i,y_i){\}}_{i=1}^N$ 由图实例和图标签对表示。此设置是归纳性的，因为在训练期间永远不会看到测试实例。此类任务的示例包括根据药物分子图的功能对其进行分类。因此，分类器 $f^{(ind)}\in F^{(ind)}:G\mapsto \gamma$ 被优化以最小化以下损失：

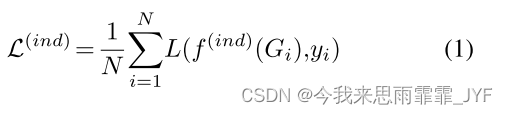
其中，$L(\cdot ,\cdot )$ 默认为交叉熵损失。

传导式节点分类：在节点分类设置中，图 $G_i$ 的目标节点 $c_i\in V_i$ 与对应的节点标签 $y_i\in \gamma$ 相关联。分类是在节点上，而不是在整个图上。我们在这里关注传导设置，其中整个数据集中仅考虑单个图 $G_0=(V_0,E_0)$。也就是说，$G_i=G_0,\forall G_i\in G$。它是传导性的，因为在训练期间也能观察到测试节点（但不包括它们的标签）。这种情况下的示例包括对 Citeseer 等引文数据库中的论文或 Facebook 等社交网络中的实体进行分类。这里数据集表示为 $D^{(tra)}=\{(G_0,c_i,y_i){\}}_{i=1}^N$，分类器 $f^{(tra)}(\cdot ;G_0)\in F^{(tra)}:V_0\mapsto \gamma$ 最小化以下损失：

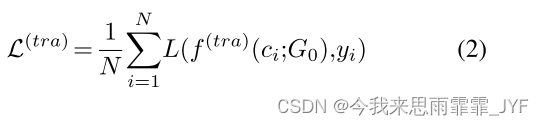
GNN 系列模型

  图神经网络 (GNN) 定义了图 $G=(V,E)$ 上神经网络的通用架构。该架构通过迭代过程获得节点的向量表示：

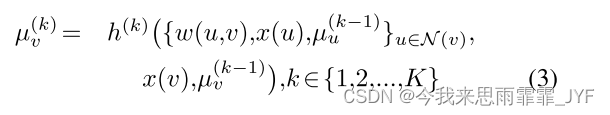
其中，$N(v)$ 为指定节点 $v\in V$ 的邻域。初始节点嵌入 ${\mu }_v^{(0)}\in R^d$ 设置为0。为了简单起见，我们将结果节点嵌入表示为 ${\mu }_v={\mu }_v^{(K)}$ 。为了从节点嵌入获得图级嵌入，在节点嵌入上应用全局池化。普通 GNN 模型运行上述迭代直至收敛。但最近人们发现，在各种应用中，使用固定的传播步骤数 $T$ 和不同的参数化能够取得良好的效果。

图对抗攻击

  给定一个学习的分类器 $f$ 和数据集中的一个实例 $(G,c,y)\in D$，图对抗攻击者 $g(\cdot ,\cdot ):G\times D\mapsto G$ 要求修改图 $G=(V,E)$ 为 $\tilde{G}=(\tilde{V},\tilde{E})$，使得：

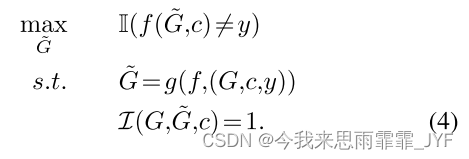
这里， I ( ⋅ , ⋅ , ⋅ ) : G × G × V ↦ { 0 , 1 } I( \cdot , \cdot , \cdot ):G \times G \times V \mapsto \{ 0,1\} I(⋅,⋅,⋅):G×G×V↦{0,1} 是一个等价指标（扰动程度），它告诉两个图 $G$ 和 $\tilde{G}$ 在分类语义下是否等价。
  在本文中，我们重点关注对离散结构的修改。攻击者 $g$ 可以在 $G$ 中添加或删除边来构造新图。这种类型的操作非常丰富，因为通过对边进行一系列修改，可以执行添加或删除节点的操作。此外，修改边比修改节点更难，因为选择一个节点只需要 $O(\left|V\right|)$ 复杂度，而选择一条边需要 $O({\left|V\right|}^2)$ 复杂度。
  由于攻击者的目的是欺骗分类器 $f$，而不是实际更改实例的真实标签，因此应首先定义等效指示符 $I(\cdot ,\cdot ,\cdot )$ 以限制攻击者可以执行的修改。我们使用两种方法来定义等效指标：

（1）显式语义。在这种情况下，假设分类器 $f^{\ast }$ 是可访问的。因此，等价指标 $I(\cdot ,\cdot ,\cdot )$ 定义为：

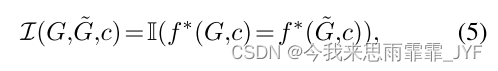
其中， Ⅱ ( ⋅ ) ∈ { 0 , 1 } ( \cdot ) \in \{ 0,1\} (⋅)∈{0,1} 是指示函数。

（2）小修改。在许多情况下，当显式语义未知时，我们会要求攻击者在邻域图中进行尽可能少的修改：

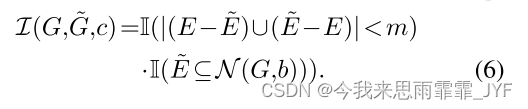
上式中，$m$ 是允许修改的最大边数，且 $N(G,b)=\{(u,v):u,v\in V,d^{(G)}(u,v)\le b\}$ 定义 $b$ 跳邻域图，其中 d ( G ) ( u , v ) ∈ { 1 , 2 , . . . } {d^{(G)}}(u,v) \in \{ 1,2,...\} d(G)(u,v)∈{1,2,...} 是图 $G$ 中两个节点之间的距离（几跳）。
  以在社交网络中为例，一个可疑的行为可能是在短时间内添加或删除许多朋友，或者与一个没有共同朋友的人建立友谊。方法（2）消除了上述两种可疑的行为，从而规范 $g$ 的行为。

作为分层强化学习的攻击

  给定一个实例 $(G,c,y)$ 和一个目标分类器 $f$，我们将攻击过程建模为一个有限时间视野马尔可夫决策过程 $M^{(m)}(f,G,c,y)$。这个 MDP 的定义如下：
操作  正如我们在第 3 节中提到的，攻击者可以添加或删除图中的边。因此，在时间步 $t$ 的单个动作是 $a_t\in A\subseteq V\times V$。然而，简单地在 $O({\left|V\right|}^2)$ 空间中执行操作的成本太高。我们很快就会展示如何使用分层操作来分解这个操作空间。
状态  时间 $t$ 的状态 $s_t$ 由元组 $({\hat{G}}_t,c)$ 表示，其中 ${\hat{G}}_t$ 是一个部分修改的图，对 $G$ 进行了一些边的添加/删除。
奖励  攻击者的目的是欺骗目标分类器。因此，只有在 MDP 结束时才会收到非零奖励，为：

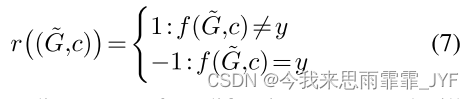
修改的中间步骤不会获得任何奖励。也就是说，对于所有 $t=1,2,...,m-1,r(s_t,a_t)=0$ ，在PBA-C设置中，如果可以访问目标分类器的预测置信度，我们还可以使用 $r(\tilde{G},c)=L(f(\tilde{G},c),y)$ 作为奖励。
结束条件  一旦代理修改了 $m$ 条边，该过程就会停止。为简单起见，我们关注固定长度的 MDP。在较少修改就足够的情况下，我们可以简单地让代理修改虚拟边。
  根据上述设置，此MDP的轨迹示例如下：$(s_1,a_1,r_1,...,s_m,a_m,r_m,s_{m+1})$ ，其中，$s_1=(G,c)$， s t = ( G ^ t , c ) , ∀ t ∈ { 2 , . . . , m } {s_t} = ({\hat G_t},c),\forall t \in \{ 2,...,m\} st​=(G^t​,c),∀t∈{2,...,m}，以及 $s_{m+1}=(\tilde{G},c)$。最后一步将获得奖励 $r_m=r(s_m,a_m)=r((\tilde{G},c))$ 并且所有其他中间奖励为0： r t = 0 , ∀ t ∈ { 1 , 2 , . . . , m − 1 } {r_t} = 0,\forall t \in \{ 1,2,...,m - 1\} rt​=0,∀t∈{1,2,...,m−1}。由于这是一个有限范围的离散优化问题，我们使用 Q-learning 来学习 MDP。在我们的初步实验中，我们还尝试了像 Advantage Actor Critic 这样的策略优化方法，但发现 Q-learning 工作得更稳定。所以下面我们重点关注 Q-learning 的建模。
  Q-learning是一种离策略（off-policy）优化方法，它直接拟合如下的贝尔曼最优方程：

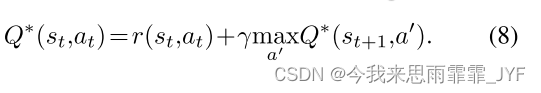
这隐含地表明了贪婪策略：

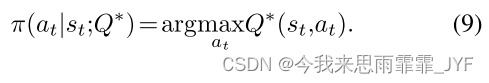
其中，$\gamma$ 固定为 1。请注意，对于大型图而言，直接在 $O({\left|V\right|}^2)$ 空间中操作操作的成本太高。因此，我们建议将 $a_t\in V\times V$ 处的动作分解为 $a_t=(a_t^{(1)},a_t^{(2)})$，其中 $a_t^{(1)},a_t^{(2)}\in V$ 。因此，单个边动作 $a_t$ 被分解为这条边的两个端点。分层 Q 函数建模如下：

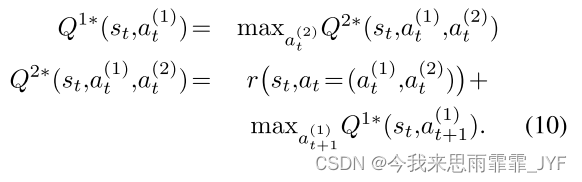
在上面的公式中，$Q^{1\ast }$ 和 $Q^{2\ast }$ 是实现原始 $Q^{\ast }$ 的两个函数。仅当选择一对 $(a_t^{(1)},a_t^{(2)})$ 时，才认为操作已完成。因此奖励只有在 $a_t^{(2)}$ 完成后才有效。很容易看出，这种分解具有与等式（8）中相同的最优结构，但执行一个动作只需要 $O(2\times \left|V\right|)=O(\left|V\right|)$ 复杂度。图 1 说明了此过程。
  进一步看一下方程（10），由于只有最后一个时间步的奖励不为零，并且给出了修改预算 $m$，因此我们可以将贝尔曼方程显式展开为：

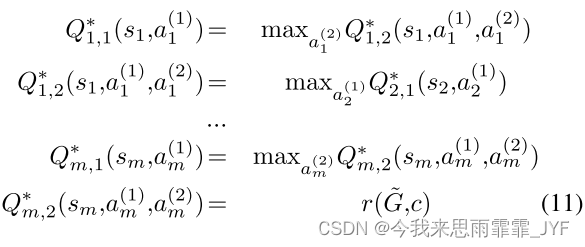
为了使符号紧凑，我们仍然使用 Q ∗ = { Q t , 1 ∣ 2 ∗ } t = 1 m {Q^*} = \{ Q_{t,1|2}^*\} _{t = 1}^m Q∗={Qt,1∣2∗​}t=1m​ 来表示 $Q$ 函数。由于数据集中的每个样本都定义了一个 MDP，因此可以为每个 MDP $M_i^{(m)}(f,G_i,c_i,y_i),i=1,...,N$ 学习单独的 $Q$ 函数。然而，我们在这里关注更实际和更具挑战性的设置，其中仅学习一个 $Q^{\ast }$。因此，要求学习到的 Q 函数对所有 MDP 进行泛化或迁移：

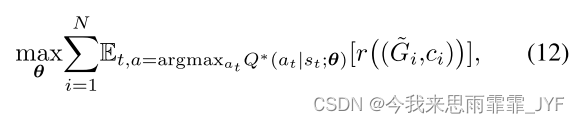
其中， $Q^{\ast }$ 由 $\theta$ 参数化。下面我们提出了这种 $Q^{\ast }$ 的参数化（原文3.1.1），它可以推广到 MDP。

其他攻击方式

  RL-S2V（ $Q^{\ast }$ 的参数化）适合黑盒攻击和迁移。然而，对于不同的攻击场景，可能会首选其他算法。我们首先在第 3.2.1 节中介绍需要最少信息的 RandSampling；然后在Sec 3.2.2中，提出了白盒攻击GradArgmax；最后，GeneticAlg是一种进化计算，在第3.2.3节中提出。

随机采样

  这是最简单的攻击方法，从图 $G$ 中随机添加或删除边。当抽样到一个边修改动作 $a_t=(u,v)$ 时，我们只有在它满足语义约束 $I(\cdot ,\cdot ,\cdot )$ 时才会接受。这需要对攻击的最少信息。尽管简单，但有时也能得到很好的攻击率。

基于梯度的白盒攻击

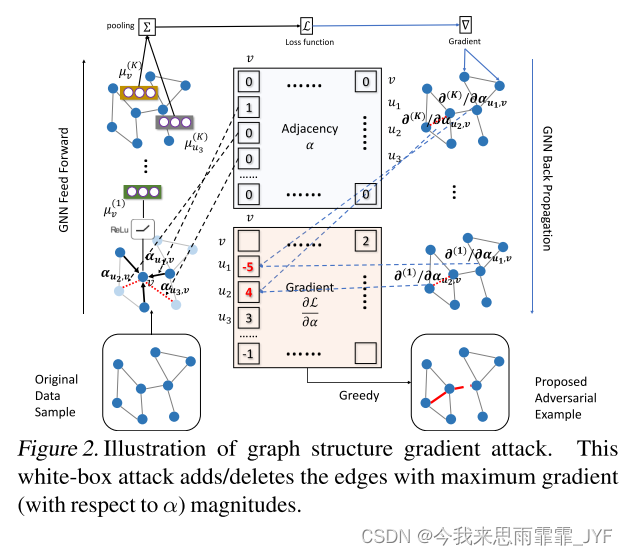
  梯度已经成功地用于修改连续输入，例如，图像。然而，针对离散结构获取梯度并非易事。回想一下方程（3）中定义的一般迭代嵌入过程，我们为每对 $(u,v)\in V\times V$ 关联一个系数 ${\alpha }_{u,v}$：

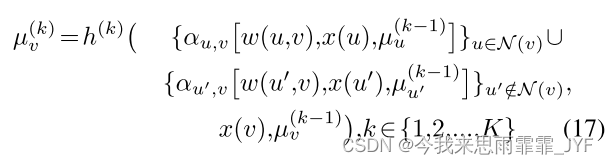
让 ${\alpha }_{u,v}$=Ⅱ$(u\in N(v))$。也就是说，$\alpha$ 本身就是二进制邻接矩阵。不难看出，上述公式与式（3）具有相同的效果。然而，这些附加系数给了我们关于每条边(存在或不存在)的梯度信息：

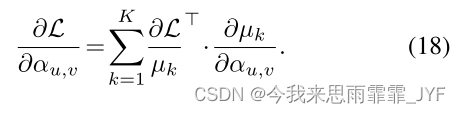
为了对模型进行攻击，我们可以进行梯度上升，即 ${\alpha }_{u,v}\leftarrow {\alpha }_{u,v}+\eta \frac{\partial L}{{\partial }_{{\alpha }_{u,v}}}$ 。然而，攻击是在一个离散的结构上，其中只允许添加或删除 $m$ 条边。这里我们需要解决一个组合优化问题：

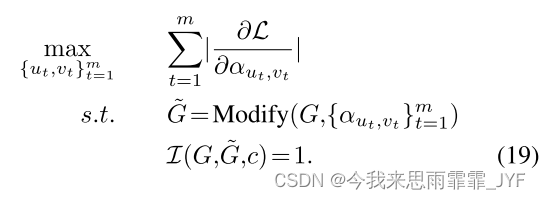
我们简单地使用贪婪算法来解决上述优化问题。这里，给定一组系数 { α u t , v t } t = 1 m \{ {\alpha _{{u_t},{v_t}}}\} _{t = 1}^m {αut​,vt​​}t=1m​ 的 $G$ 的修改是通过顺序修改图 ${\hat{G}}_t$ 的边 $(u_t,v_t)$ 来执行的：

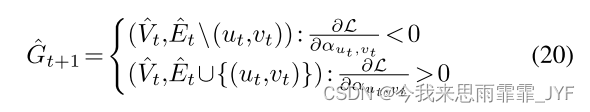
也就是说，我们修改最有可能导致目标发生变化的边。根据梯度的符号，我们添加或删除边。我们将其命名为 GradArgmax，因为它基于梯度信息进行贪婪选择。
  攻击流程如图2所示。由于这种方法需要梯度信息，因此我们将其视为白盒攻击方法。此外，梯度考虑了图中的所有节点对，计算成本至少为 $O({\left|V\right|}^2)$，不包括等式（18）中梯度的反向传播。如果没有进一步的近似，这种方法无法扩展到大图。

遗传算法

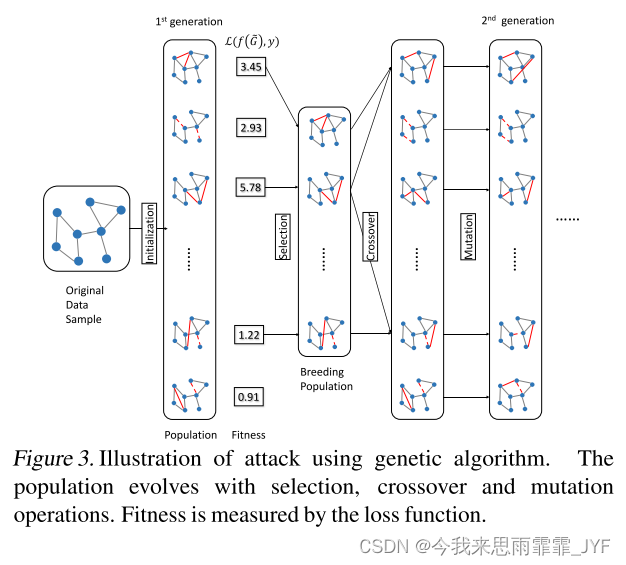
  进化计算已成功应用于许多零阶优化场景，包括神经结构搜索和图像的对抗攻击。在这里，我们提出了一种实现遗传算法类型的黑盒攻击方法。给定一个实例 $(G,c,y)$ 和目标分类器 $f$，该算法涉及五个主要组成部分，如下所述：
总体：总体是指候选解的集合。
适应度：当前群体中的每个候选解决方案都会获得一个衡量解决方案质量的分数。我们使用目标模型的损失函数作为得分函数。一个好的攻击解决方案应该会增加这种损失。由于适应度是一个连续分数，因此它不适用于仅可访问分类标签的 PBA-D 设置。
选择：给定当前种群的适应度分数，我们可以进行加权采样或贪心选择来选择下一代的“繁殖”种群 $P_b^{(r)}$。
交叉：选择 $P_b^{(r)}$ 后，我们随机选择两个候选图并通过混合这两个候选的边来进行交叉。
突变：突变过程也是受生物学启发的。

实验

  对于 GeneticAlg，我们设置种群大小 $\left|P\right|=100$，轮数 $R=10$。我们将交叉率和变异率调整为{0.1,…,0.5}。对于RL-S2V，我们调整其S2V模型的传播次数K={1,…,5}。GradArgmax 和 RandSampling 没有参数调整。

图攻击

  三分类图任务，其中每个类包含 5,000 个图，共15,000个图。因此图中最多可以有 3 个分量。请参见图 4 进行说明。数据集分为训练集和两个测试集。测试集 I 包含 1,500 个图，而测试集 II 包含 150 个图。每个集合包含来自不同类的相同数量的实例。

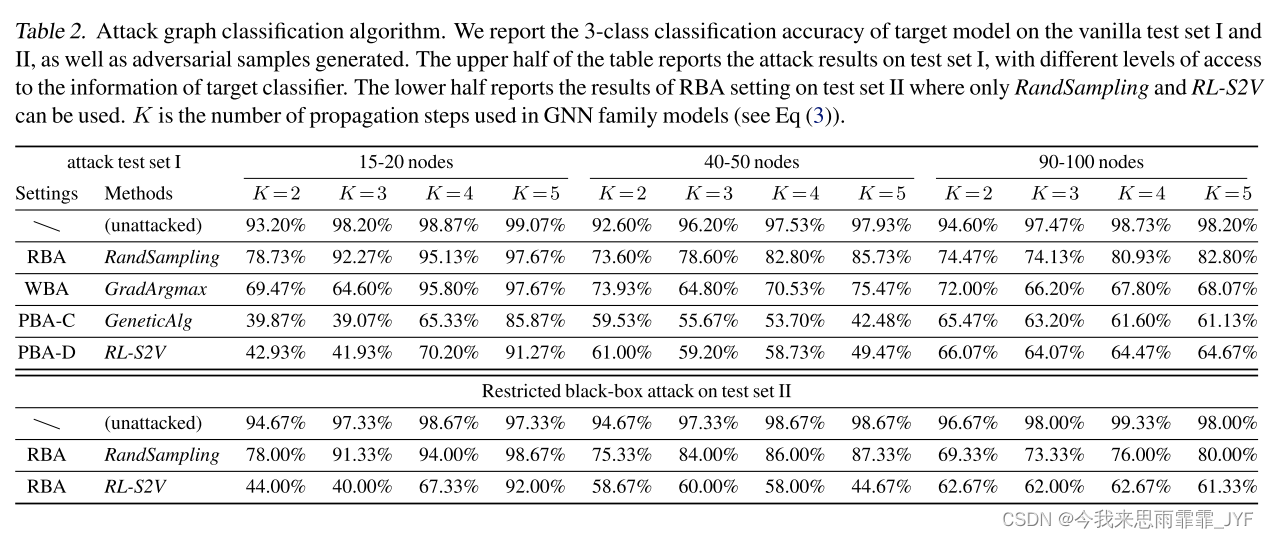
  我们选择 structure2vec 作为攻击的目标模型。表 2 显示了不同设置的结果。对于测试集 I，我们可以看到 Structure2vec 在区分连接组件的数量方面实现了非常高的准确度。在大多数情况下，增加 K 似乎可以提高泛化能力。然而，我们可以看到，在实际的黑盒攻击场景下，GeneticAlg 和 RL-S2V 可以将准确率降低至 40% ∼ 60%。在攻击图分类算法时，GradArgmax 似乎不是很有效。
  对于测试集 II 上的限制黑盒攻击（参见表 2 的下半部分），要求攻击者在不访问目标模型的情况下提出对抗性样本。由于 RL-S2V 是在测试集 I 上学习的，因此它能够将其学习的策略转移到测试集 II。这表明目标分类器犯了某种形式的一致错误。

  该实验表明，（1）监督图问题确实存在对抗性例子；（2）具有良好泛化能力的模型仍然会遭受对抗性攻击； (3) RL-S2V 可以学习可转移的对抗策略来攻击未见过的图。

节点级攻击

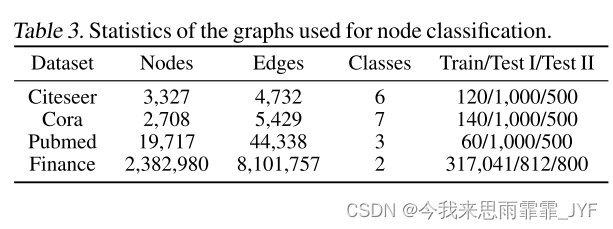
  在这个实验中，我们想要检查对节点分类问题的对抗性攻击。与第 4.1 节不同，这里的设置是直通式的，在训练期间也可以看到测试样本（但看不到它们的标签）。这里我们使用四个真实世界的数据集，即 Citeseer、Cora、Pubmed 和 Finance。前三个是通常用于节点分类的小规模引文网络，其中每个节点都是具有相应词袋特征的论文。最后一个是一个大规模数据集，包含电子商务一天内的交易，其中节点集包含买家、卖家和信用卡。要求分类器区分正常交易和异常交易。每个数据集的统计数据如表3所示。节点还包含不同维度的特征。我们使用 GCN 作为攻击的目标模型。这里的“小修改”是用来规范攻击者的。也就是说，给定图 G 和目标节点 c，对抗样本仅限于删除节点 c 2 跳内的单条边。

  结果如表4所示。我们可以看到，虽然删除单条边是对图可以做的最小修改，但在这些小图上的攻击率仍然约为 10%，在 Finance 数据集中为 4%。我们还进行了详尽的攻击作为健全性检查，这是任何算法在攻击预算下可以做到的最好的。如果允许修改两条边，分类器准确率将降低至 60% 或更低。然而，考虑到图中的平均度并不大，删除两条或更多条边将违反“小修改”约束。我们需要小心，只创建对抗性样本，而不是实际更改该样本的真实标签。

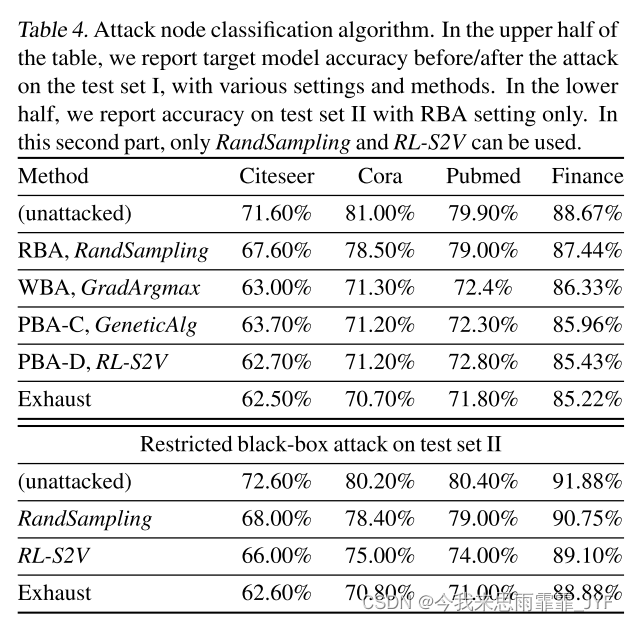
  在这种情况下，GradArgmax 表现得很好，这与图级攻击的情况不同。这里关于邻接矩阵 $\alpha$ 的梯度不再被平均，这使得更容易区分有用的修改。对于测试集 II 上的限制黑盒攻击，RL-S2V 仍然学习泛化到未见过的样本的攻击策略。尽管我们在现实数据集中没有黄金分类器（替代模型），但提出的对抗样本很可能是有效的：(1)结构修改微小且在2-hop以内； (2)我们没有修改节点特征。

对抗样本的检查

  在本节中，我们将不同攻击者提出的对抗样本可视化。RL-S2V针对图级分类问题提出的解决方案如图5所示。真实标签为 1, 2, 3，而目标分类器错误地预测为 2, 1, 2。在图 5(b) 和 © 中，RL 代理连接两个相距 4 跳的节点（添加红边之前）。这表明，虽然目标分类器struct2vec是用K=4训练的，但它并没有有效地捕获4跳信息。图 5(a) 还显示，即使连接距离只有 2 跳的节点，分类器也会出错。

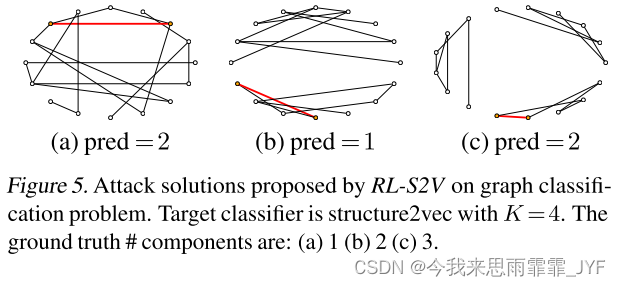
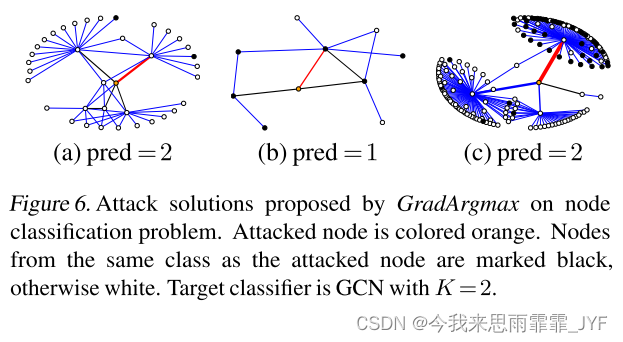
  图6展示了GradArgmax提出的解决方案。橙色节点是攻击的目标节点。GradArgmax 建议添加蓝色的边，删除黑色的边。黑色节点与橙色节点有相同的节点标签，而其他节点则没有。边缘越厚，梯度的大小就越大。图 6(b) 删除了一个具有相同标签的邻居，但仍然有其他黑色节点连接。在这种情况下，图卷积网络（GCN）表现出过度敏感。图中 6（c） 图中的错误是合理的，因为虽然红色边没有连接具有相同标签的两个节点，但它连接到了一个距离为 2 跳的同一类别的大型节点社区。在这种情况下，GCN 的预测是合理的。

防御攻击

  与图像不同，由于节点数目有限，这里可能的图结构数量也是有限的。因此，通过将对抗样本重新添加到进一步的训练中，可以期望提高目标模型的鲁棒性。例如，在第4.1节的实验中，添加对抗样本进行训练等同于增加训练集的大小，这肯定是有益的。因此，我们在这里寻求使用一种经济的对抗训练方法——在训练过程中简单地执行边删除以进行防御。
  训练期间丢弃边与 Dropout 不同。Dropout 对隐藏层中的神经元进行操作，而边 drop 则修改离散结构。它也不同于简单地删除整个隐藏向量，因为删除一条边可能会影响多个边。例如，GCN 计算归一化图拉普拉斯算子。因此，删除单条边后，需要重新计算某些条目的归一化图拉普拉斯算子。这种方法与 Hamilton 等人的方法类似，他在训练期间对固定数量的社区进行采样以提高效率。在这里，我们在每个训练步骤中全局随机丢弃边。
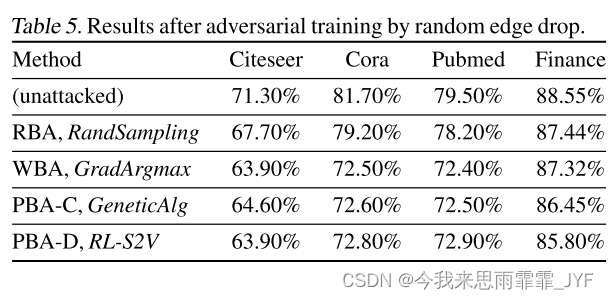
  对抗训练后的新结果如表 5 所示。从表中我们可以看出，虽然目标模型的准确率保持相似，但各种方法的攻击率下降了约1%。尽管改进的规模并不显着，但这种廉价的对抗性训练显示出了一定的有效性。

结论

  在本文中，我们研究了图结构化数据的对抗性攻击。为了执行有效的攻击，我们针对三种不同的攻击设置分别提出了三种方法，即 RL-S2V、GradArgmax 和 GeneticAlg。我们证明了一系列 GNN 模型很容易受到此类攻击。通过可视化攻击样本，我们还可以检查目标分类器。我们还通过实验讨论了防御方法。我们未来的工作包括开发更有效的防御算法。