题目: 串联所有单词的子串(1中等)
描述:
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
leetcode链接
方法一:滑动窗口
我们定义一个长度为p.size()大小的窗口,在s中不断移动此大小固定的窗口,并且比较窗口内的元素是否由p中的元素组成,考虑到题目给出的字符串都是由26个小写的字母组成因此,我们比较窗口内的元素,可以统计窗口内每个字母出现的次数,和p中每个字母出现的次数是否相同,如果相同,那么此窗口即为所求子串,因此我们定义两个大小为26的vector1和vector2,分别存储窗口中单词出现的次数和p中单词出现的次数。
时间复杂度:o(m+(n-m)*26) 需要o(m)来初始化vector存储单词的数量,后面有n-m个窗口,因此需要比较n-m次单词的数量,每次比较需要比较26个元素,因此时间复杂度为o((n-m)*26)
空间复杂度:o(1) 只需要常量级的空间
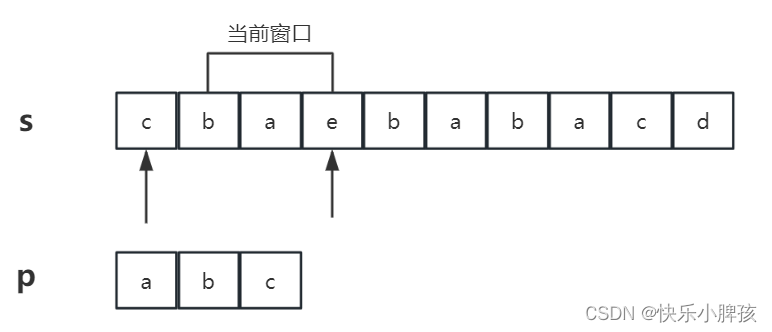
我们先统计第一个窗口的字母数量,再循环统计后面窗口的字母数量,如图所示,一边删除前一个单词(第一个指针),一边增加后一个窗口字母(后一个指针),即可得到当前指针内窗口字母的数量
vector<int> findAnagrams(string s, string p) {int n = s.size();int m = p.size();vector<int> ans;//s的大小小于p时候,肯定不存在满足条件子串if(n<m){return ans;}vector<int> sCount(26,0);vector<int> pCount(26,0);//先统计第一个窗口单词出现的次数for(int i=0;i<m;i++){sCount[s[i]-'a']++;pCount[p[i]-'a']++;}//比较第一个窗口是否为所求子串if(sCount==pCount){ans.push_back(0);}for(int i=0;i<n-m;i++){//统计下一个窗口的字母数量sCount[s[i]-'a']--;sCount[s[i+m]-'a']++;if(sCount==pCount){ans.push_back(i+1);}}return ans;
}
方法二:
考虑我们方法一花费的时间主要在滑动窗口每种字母数量与p的对比上,因此我们方法二不再统计每个窗口的字母数量,我们存储滑动窗口和p的每种单词的数量差值,并且用differ记录数量不一样的字母的个数,那么如果differ=0,表示所有字母的数量都相同,那么该窗口即为所求窗口,因此我们通过判断differ是否为0来判断是否为子串,省去了判断每一种字母数量的时间。
时间复杂度:o(m+n-m) o(m)用来初始化vector,后面有n-m个窗口需要比较,比较的时间复杂度为o(1)
空间复杂度:o(1) 申请了常量级的空间
vector<int> findAnagrams(string s, string p) {int n = s.size();int m = p.size();vector<int> ans;if(n<m){return ans;}vector<int> count(26,0);for(int i=0;i<m;i++){count[s[i]-'a']++;count[p[i]-'a']--;}int differ = 0;for(int i=0;i<26;i++){//统计第一个窗口不同数量字母的个数if(count[i]!=0){differ++;}}if(differ == 0){//如果没有则第一个窗口即为所求的子串ans.push_back(0);}for(int i=0;i<n-m;i++){if (count[s[i] - 'a'] == 1) { // 窗口中字母 s[i] 的数量与字符串 p 中的数量从不同变得相同--differ;} else if (count[s[i] - 'a'] == 0) { // 窗口中字母 s[i] 的数量与字符串 p 中的数量从相同变得不同++differ;}--count[s[i] - 'a'];if (count[s[i + m] - 'a'] == -1) { // 窗口中字母 s[i+pLen] 的数量与字符串 p 中的数量从不同变得相同--differ;} else if (count[s[i + m] - 'a'] == 0) { // 窗口中字母 s[i+pLen] 的数量与字符串 p 中的数量从相同变得不同++differ;}++count[s[i + m] - 'a'];if(differ==0){ans.push_back(i+1);}}return ans;
}
题目: 串联所有单词的子串(2困难)
描述:
给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。
s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。
例如,如果 words = [“ab”,“cd”,“ef”], 那么 “abcdef”, “abefcd”,“cdabef”, “cdefab”,“efabcd”, 和 “efcdab” 都是串联子串。 “acdbef” 不是串联子串,因为他不是任何 words 排列的连接。
返回所有串联子串在 s 中的开始索引。你可以以 任意顺序 返回答案。
示例 1:
输入:s = “barfoothefoobarman”, words = [“foo”,“bar”]
输出:[0,9]
解释:因为 words.length == 2 同时 words[i].length == 3,连接的子字符串的长度必须为 6。
子串 “barfoo” 开始位置是 0。它是 words 中以 [“bar”,“foo”] 顺序排列的连接。
子串 “foobar” 开始位置是 9。它是 words 中以 [“foo”,“bar”] 顺序排列的连接。
输出顺序无关紧要。返回 [9,0] 也是可以的。
leetcode链接
方法一:
类似于上题的方法二,我们用differ记录窗口单词出现次数和words中出现次数之差,如果differ为空,那么说明窗口中的单词和words中的单词相同。
定义n为words的大小,m为words中每个单词的长度,ls为s字符串的长度,那么每个窗口的长度应该为nm。首先我们需要将字符串s分成单词组,即分成一组有长度为m的单词组成的单词组,那么应该有m种分法,这里解释一下为什么是m种:假如字符串0123456按两个一分,那么有0 12 34 56和01 23 45 6这两种分法,如果按三个一分,那么有0 123 456和01 234 56和0123 456这三种分法,以此类推字符串按m个一分一共有m种分法,然后对于这里的每一种分法我们进行滑动窗口,来判断当前窗口是否为所求的子串,窗口一次移动一个单词的长度,即为移动m,那么即为左边减去一个单词,右边加上一个单词。
时间复杂度:o(lsm) 一共有m种分法,每一种分法我们都需要利用滑动窗口,而滑动窗口的时间复杂度为o(ls),所以总时间复杂度为o(lsm)
空间复杂度:o(nm) 一共m种分法,每一种都需要定义大小为n的unordered_map
vector<int> findSubstring(string s, vector<string>& words) {int n = words.size();int m = words[0].size();int ls = s.size();vector<int> ans;//枚举每一种单词组合的起始位置 for(int i=0;i<m&&i+n*m<=ls;i++){unordered_map<string,int> differ;for(int j = 0;j<n;j++){//统计窗口中单词出现的次数 differ[s.substr(i + j * m, m)]++;}for(int j=0;j<n;j++){//如果窗口中单词出现的次数和words中一样,那么在differ中删去 if(--differ[words[j]]==0){differ.erase(words[j]);}}//ls-m*n为剩余的字母数量,滑动窗口,每次移动一个单词的长度 for(int start=i;start<ls-m*n+1;start+=m){if(start!=i){//右边加入一个单词 string word = s.substr(start+(n-1)*m,m);if(++differ[word]==0){differ.erase(word);}//左边减去一个单词 word = s.substr(start-m,m);if(--differ[word]==0){differ.erase(word);}}//如果窗口中所有单词出现的次数和words一样则为所求子串 if(differ.empty()){ans.push_back(start);}}}return ans;
}









)





)

)

