【113】路径总和II
【105】从前序与中序遍历序列构造二叉树

1.【113】路径总和II

1.1 题目描述

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

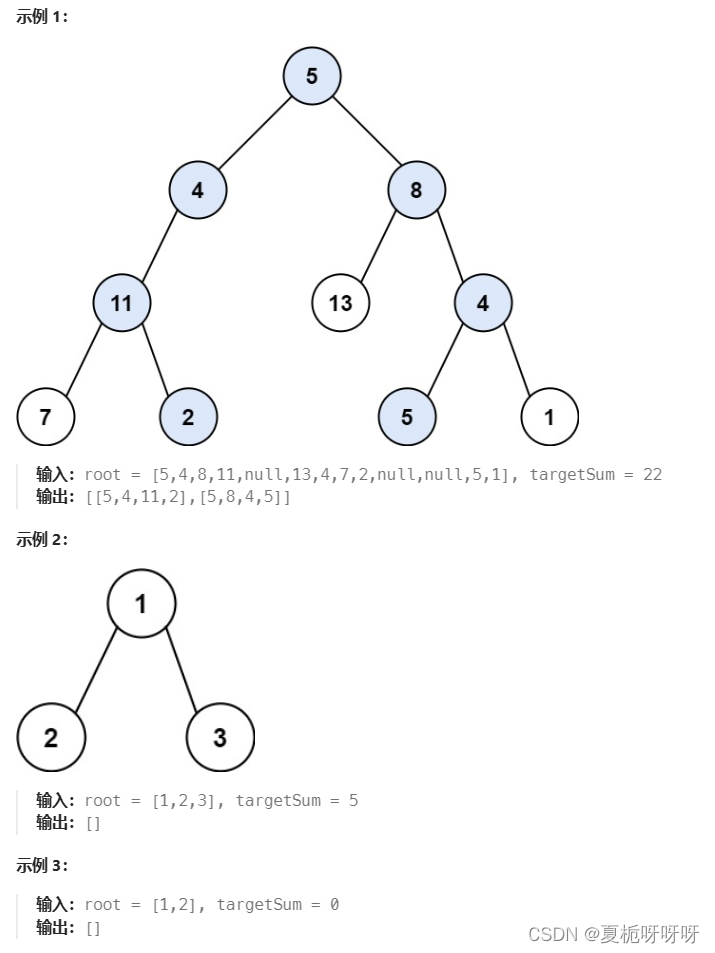
提示：

• 树中节点总数在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

1.2 解题思路

此题要遍历整个树，找到所有路径，所以递归函数不要返回值

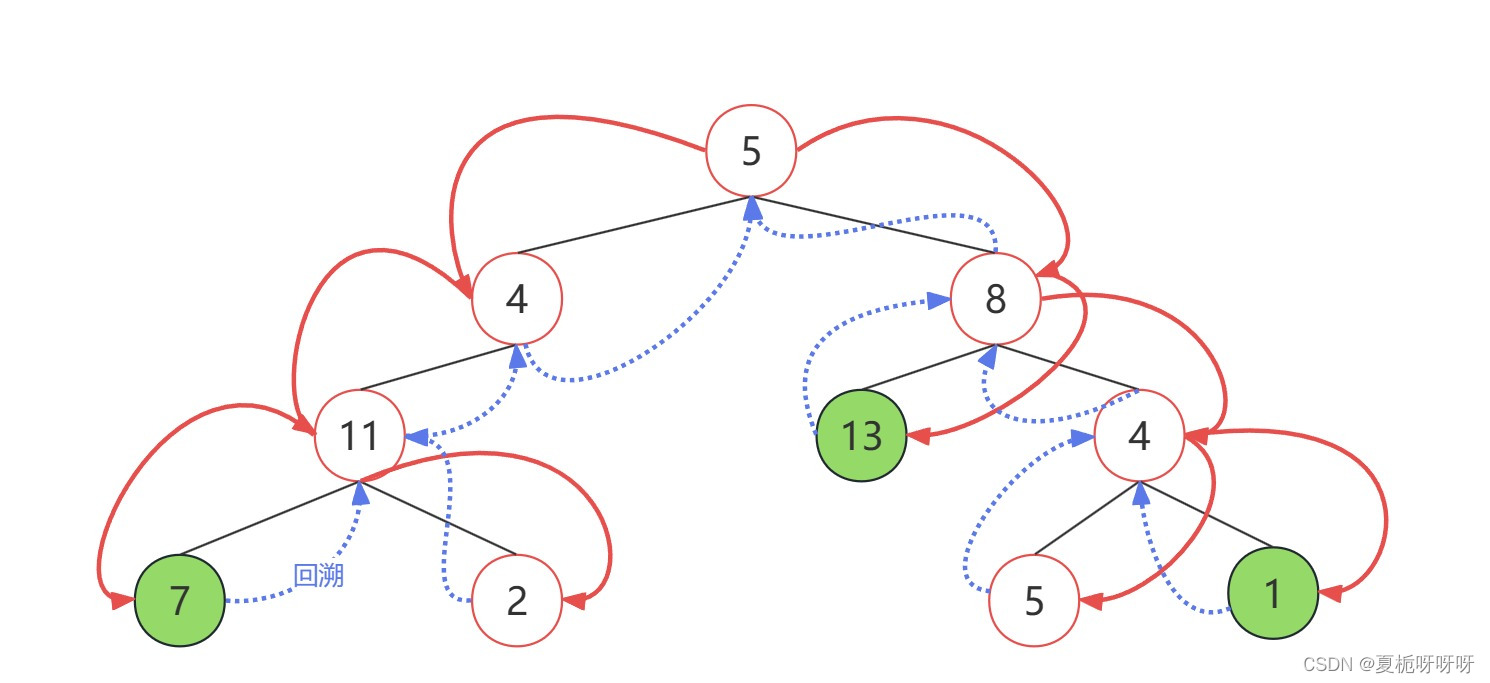
1.3 java代码实现

class Solution {List<List<Integer>> result;LinkedList<Integer> path;public List<List<Integer>> pathSum(TreeNode root, int targetSum) {result=new LinkedList<>();path=new LinkedList<>();travesal(root,targetSum);return result;}public void travesal(TreeNode root,int count){if (root==null) return;path.offer(root.val);count-=root.val;if (root.left==null && root.right==null && count==0){result.add(new LinkedList<>(path));}travesal(root.left,count);travesal(root.right,count);path.removeLast();//回溯}
}

2.【105】从前序与中序遍历序列构造二叉树

2.1 题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

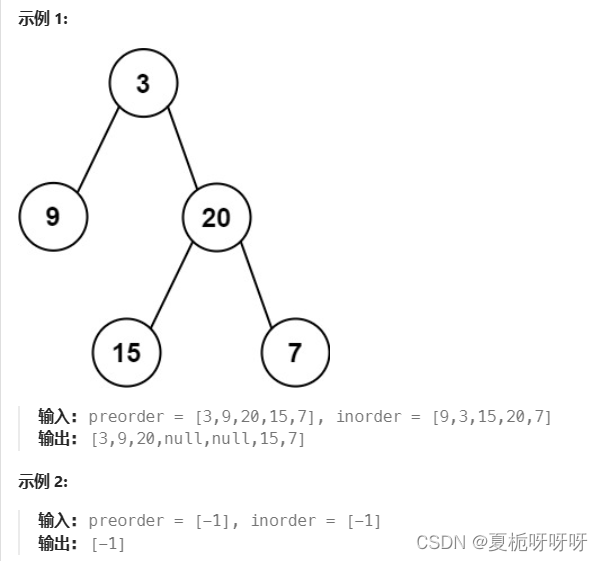
提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

2.2 java代码实现

class Solution {Map<Integer,Integer> map;//方便根据数值查找位置public TreeNode buildTree(int[] preorder, int[] inorder) {map=new HashMap<>();// 用map保存中序序列的数值对应位置for (int i=0;i<inorder.length;i++){map.put(inorder[i],i );}return findNode(preorder,0,preorder.length,inorder,0,inorder.length);}public TreeNode findNode(int[] preorder,int preBegin,int preEnd,int[] inorder, int inorderBegin, int inorderEnd){//参数里的范围都是左闭右开if (inorderBegin>=inorderEnd || preBegin>=preEnd){return null;}// 找到前序遍历的最后一个元素在中序遍历中的位置int rootIndex=map.get(preorder[preBegin]);TreeNode root=new TreeNode(inorder[rootIndex]);//构造节点//保存中序左子树个数，用来确定前序数列的个数int lenOfleft=rootIndex-inorderBegin;root.left=findNode(preorder,preBegin+1,preBegin+lenOfleft+1,inorder,inorderBegin,rootIndex);root.right=findNode(preorder,preBegin+lenOfleft+1,preEnd,inorder,rootIndex+1,inorderEnd);return root;}
}