题目要求:
给定一个大小为 m x n 的二进制矩阵,并且允许您以任意顺序重新排列矩阵的列。
对列进行最佳重新排序后,返回矩阵中每个元素都为 1 的最大子矩阵的面积。

输入:矩阵 = [[0,0,1],[1,1,1],[1,0,1]]
输出:4
说明:您可以重新排列列,如上所示。
最大的 1 子矩阵(粗体)的面积为 4。
思路
因为可以改变列的结构,而无法改变矩形的高度,因此可以先计算每个1在矩形中贡献了多少高度。让我们修改矩阵,使每个矩阵[行][列]代表以下值:“如果我们从矩阵[行][列]开始向上移动,有多少个连续的1?”
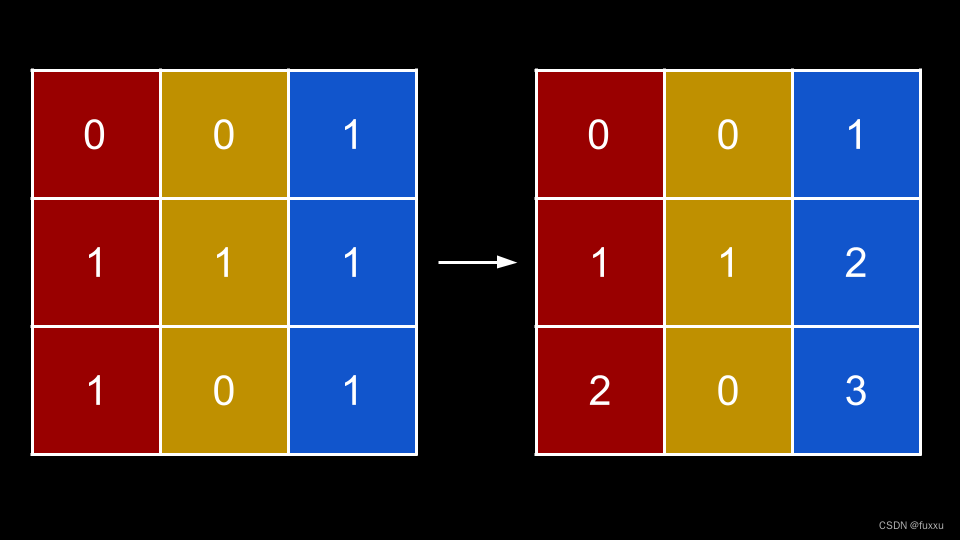
这次修改的意义何在?现在,我们可以考虑每列在给定行上可以贡献多少高度。看一下底行 [2, 0, 3]。如果我们按降序排序会发生什么?
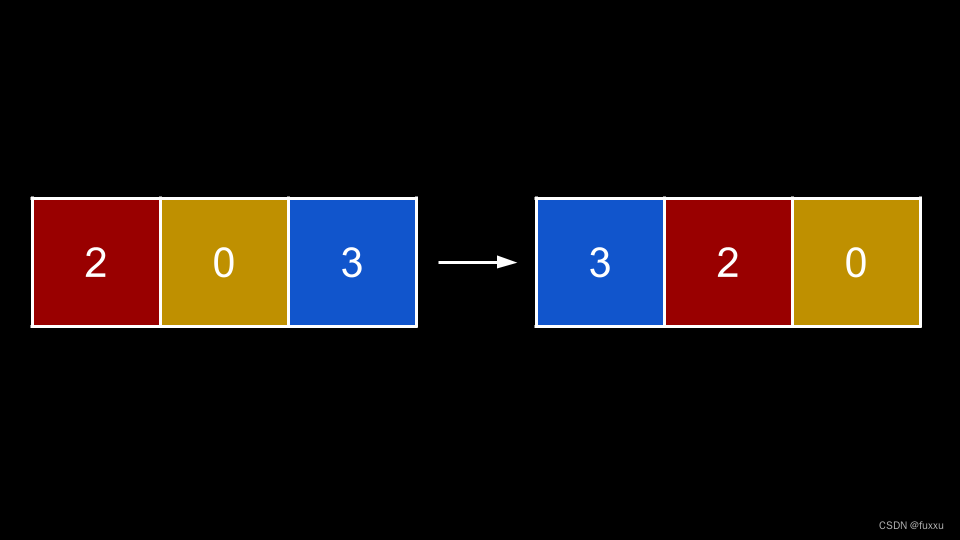
这个排序行 [3, 2, 0] 表示:
- 在第 0 列,我们看到了三个连续的。
- 在第 1 列,我们看到两个连续的。
- 在第 2 列,我们看到了零个连续的。
从视觉上看,这个排序的行代表以下图像:
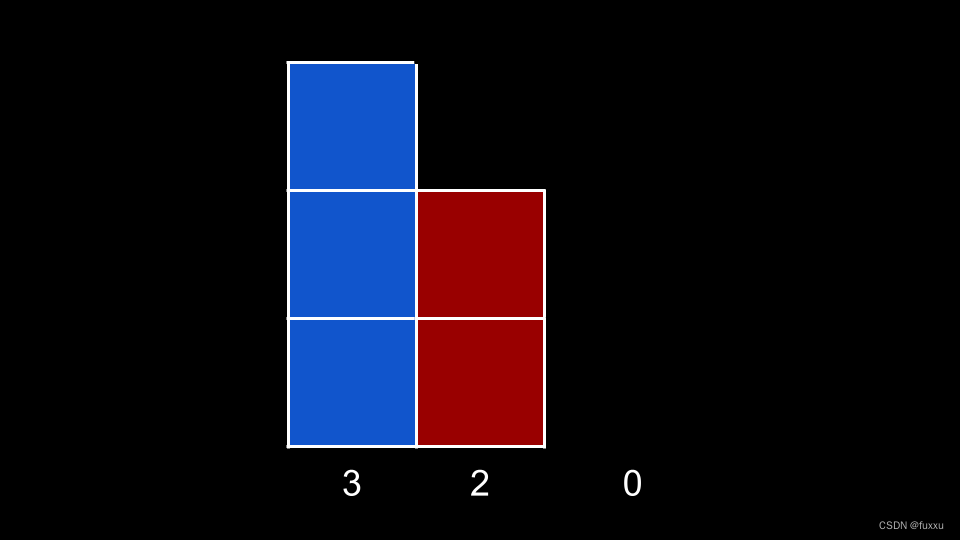
现在,希望这个想法很清楚:在每一列 col,我们知道其左侧的每一列的高度都大于或等于当前高度。 这样,我们就可以以列数col+1为基,构成一个当前高度的子矩阵。
我们迭代输入矩阵并跟踪每列出现了多少个连续的矩阵。 为此,对于给定的行 col,我们首先检查矩阵 [行] [列] != 0。如果是,我们将矩阵 [行 - 1] [列] 的值添加到其中。 如果matrix[row][col] = 0,我们什么都不做,这会有效地重置当前列的条纹,因为matrix[row + 1][col]的下一次迭代将引用matrix[row][col],即 0. 如果我们有一个条纹,那么矩阵[行][列]将每行连续增加1。
一旦我们完成了一行的更新,我们就将其降序排序并迭代它,以找到如果我们将当前行视为子矩阵的底部则可以制作的最大子矩阵。 对于排序的 currRow,我们将 currRow[i] 视为高度,将 i + 1 视为基数。 之所以允许我们对每一行进行排序,是因为对每一行进行排序相当于重新排列列,而我们可以自由地这样做。
class Solution {
public:int largestSubmatrix(vector<vector<int>>& matrix) {int ans = 0;for (int i = 0; i < matrix.size(); ++i) {for (int j = 0; j < matrix[0].size(); ++j) {if (matrix[i][j] != 0 && i > 0) {matrix[i][j] = matrix[i-1][j] + 1;}}vector<int> currRow = matrix[i];sort(currRow.begin(), currRow.end(), greater());for (int j = 0; j < matrix[0].size(); ++j) {ans = max(ans, currRow[j] * (j+1));}}return ans;}
};时间复杂度: O(m⋅n⋅logn)
我们迭代 m 行。 对于每一行,我们更新值的成本为 O(n)。 然后,我们对行进行排序,其成本为 O(n⋅logn)。 最后,我们迭代该行来计算子矩阵面积,其成本为 O(n)。
总的来说,每次 m 迭代的成本为 O(n⋅logn)。
空间复杂度: O(m⋅n)
虽然我们只分配大小为 O(n) 的 currRow,但我们正在修改矩阵。 修改输入通常被认为是一种不好的做法,当你这样做时,你应该将其计入空间复杂度的一部分。
这个题目考察的不是算法或者计算速度,而是把矩形面积转换成列的之前有多少个连续1作为矩形的高的思路(类似dp)。
















)


