【华为OD】B\C卷真题:100%通过:找城市 C/C++实现
题目描述:
一张地图上有n个城市,城市和城市之间有且只有一条道路相连:要么直接相连,要么通过其它城市中转相连(可中转一次或多次)。城市与城市之间的道路都不会成环。
当切断通往某个城市 i 的所有道路后,地图上将分为多个连通的城市群,设该城市 i 的聚集度为 DPi(Degree of Polymerization), DPi = max(城市群1的城市个数, 城市群2的城市个数, ... 城市群m的城市个数)。
请找出地图上 DP 值最小的城市(即找到城市 j,使得 DPj = min(DP1, DP2 ... DPn) )
提示:如果有多个城市都满足条件,这些城市都要找出来(可能存在多个解)
提示:DPi 的计算,可以理解为已知一棵树,删除某个节点后,生成的多个子树,求解多个子树节点数的问题。
输入描述
每个样例:第一行有一个整数N,表示有N个节点。1<=N<=1000
接下来的N-1行每行有两个整数x,y,表示城市x与城市y连接。1<=x, y<=N
输出描述
输出城市的编号。如果有多个,按照编号升序输出。
示例1
输入输出示例仅供调试,后台判题数据一般不包含示例
输入
5
1 2
2 3
3 4
4 5
输出
3
说明
输入表示的是如下地图:
![]()
对于城市3,切断通往3的所有道路后,形成2个城市群[(1,2),(4,5)],其聚集度分别都是2。DP3 = 2。 对于城市4,切断通往城市4的所有道路后, 形成2个城市群[ (1,2,3), (5) ],DP4 = max(3, 1)= 3 。依次类推,切断其它城市的所有道路后,得到的DP都会大于2,因为城市3就是满足条件的城市,输出是3。
示例2
输入输出示例仅供调试,后台判题数据一般不包含示例
输入
6
1 2
2 3
2 5
3 4
3 6
输出
2 3
说明
输入表示的是如下地图:
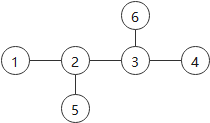
切断通往2的所有道路后,形成3个城市群[(1),(5),(3,4,6)],其聚集度分别都是1、1、3,因此DP2 = 3。
切断通往3的所有道路后,形成3个城市群[(1,2,5),(4),(,6)],其聚集度分别都是3、1、1,因此DP3 = 3。
切断其它城市的所有道路后,得到的DP都会大于3,因为城市2、3就是满足条件的城市,升序排列输出是2 3
解题思路:
其实就是构建多叉树来实现即可
代码实现:
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <map>using namespace std;struct Node {int val;int par;vector<Node *> childs;
};void sort(vector<int> &xPos, vector<int> &yPos, int n) {for (int i = 0; i < n; i++) {if (xPos[i] > yPos[i]) {swap(xPos[i], yPos[i]);}}for (int i = 0; i < n; i++) {for (int j = 0; j < n - i - 1; j++) {if ((xPos[i] > xPos[i + 1]) || (xPos[i] == xPos[i + 1] && yPos[i] > yPos[i + 1])) {swap(xPos[i], xPos[i + 1]);swap(yPos[i], yPos[i + 1]);}}}
}void mergeNode(Node *pCity, Node *cCity) {cCity->par = pCity->val;pCity->childs.push_back(cCity);for (Node *city : cCity->childs) {city->par = pCity->val;pCity->childs.push_back(city);}cCity->childs.clear();
}int main() {int n;cin >> n;vector<int> xPos(n, 0);vector<int> yPos(n, 0);for (int i = 1; i < n; i++) {cin >> xPos[i] >> yPos[i];}if (n == 1) {cout << 1 << endl;}else if (n == 2) {cout << 1 << endl;cout << 2 << endl;}else {sort(xPos, yPos, n);int min = 1008;int max;int totalCity;vector<int> minArr;for (int i = 1; i <= n; i++) {vector<Node *> citys(n + 1);max = 0;for (int j = 1; j <= n; j++) {Node *city = new Node();city->par = j;city->val = j;citys[j] = city;}for (int j = 1; j < n; j++) {if (xPos[j] == i || yPos[j] == i) {continue;}Node *yCity = citys[yPos[j]];Node *xCity = citys[xPos[j]];if (xCity->par != xCity->val) {xCity = citys[xCity->par];}if (yCity->par == yCity->val) {mergeNode(xCity, yCity);}else {Node *yCityParent = citys[yCity->par];mergeNode(xCity, yCityParent);}}for (int j = 1; j <= n; j++) {if (citys[j]->par == citys[j]->val) {totalCity = citys[j]->childs.size() + 1;max = max < totalCity ? totalCity : max;}}if (min > max) {min = max;minArr.clear();minArr.push_back(i);}else if (min == max) {minArr.push_back(i);}for (int m = 0; m < citys.size(); ++m) {delete citys[m];}}string ans = "";for (int k = 0; k < minArr.size(); ++k) {ans += to_string(minArr[k]) + " ";}cout << ans << endl;}
}







)


)







