决策树（第四周）

一、决策树基本原理

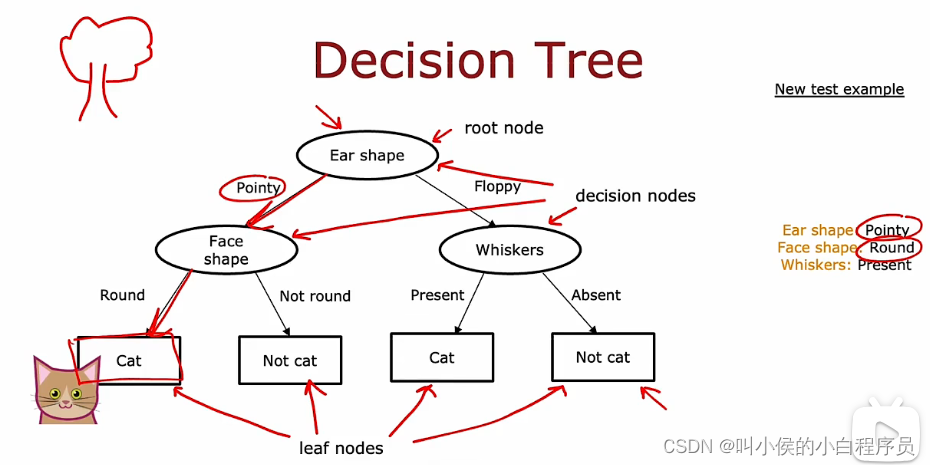
如下图所示，是一个用来辨别是否是猫的二分类器。输入值有三个（x1，x2，x3）=（耳朵形状，脸形状，胡须），其中x1={尖的，圆的}，x2={圆脸，不是圆脸}，x3={有胡须，没有胡须}，这三个输入值都是1/0。输出y=1表示是猫，否则不是猫。

椭圆型称为决策节点，矩形称为叶节点，下图模型称为决策树。

对于同一个问题，可以有许多个不同的决策树模型，如下图所示。我们需要做的就是选出最优的模型，让他在交叉验证集上表现最优，这就是决策树学习算法。

1.1 学习过程

1、决定在根节点使用什么特征。根据这个特征将训练数据划分到两个分支。假如选择耳朵形状：

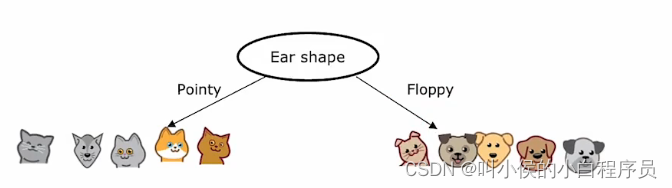
2、先关注左侧分支，再根据算法选择出新的决策特征（算法后面讲解）。假如选择面部形状：

注意到左侧的四个训练数据都是猫，接下来不用再选择新特征进行分裂，将这个节点转化成叶节点。同理右侧节点：

3、接下来看右侧分支，再利用算法决策出一个合适的特征进行分裂，假如是胡须，后面的操作同上：

1.2 一般步骤

1、在每一个决策节点上选择出合适的特征进行分裂，这个特征必须将子集尽量最大化纯度（也就是说，这个子集当中，尽量都是猫或者都不是猫）。下图是分别将三个特征作为根节点进行分类的结果：

2、决定何时停止分裂

当子集纯度达到100% （也就是说，一个子集中只有一个类别）
当分类节点已经达到最大的允许深度，则停止分裂。（限制决策树深度的一个原因是确保我们的树不会变得太大和笨重，其次，通过保持树小，它不太容易过度拟合）
当纯度已经低于阈值
当决策节点的示例数量低于阈值

1.3 纯度purity

1.3.1 熵

熵可以用来量化纯度，越小表示纯度越高。

P1表示所有子集中猫的占有比例，下图的曲线图是熵随着P1变化的曲线图，横轴表示P1，数据范围在0-1，纵轴表示熵，数据范围在0-1。只有当P1很大或者很小时，熵会很小。

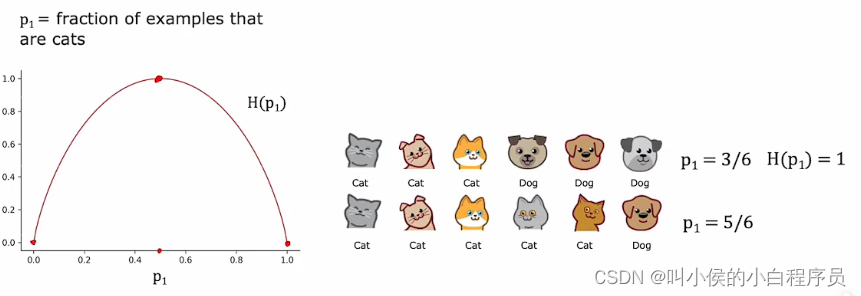
下图是熵的计算公式：

1.4 选择拆分信息增益

在构建决策树时，我们决定在节点上拆分哪个特征，将基于哪种特征选择最能减少熵（最大化纯度）。熵的减少称为信息增益。下图是选择不同特征进行分类后，各个分支的熵：

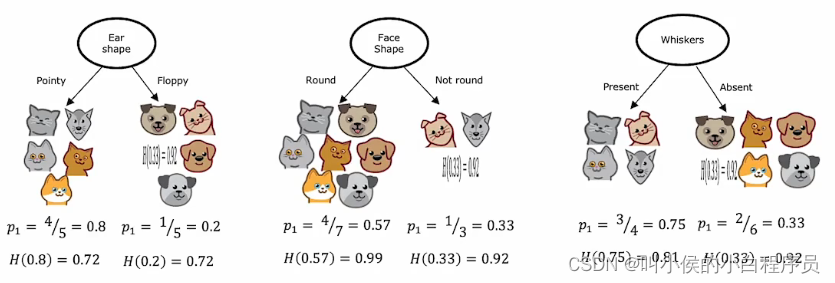
接下来我们需要一个标准来衡量哪种决策方式最好。如果熵很大，分裂子集也很大，这意味着子集中有很多复杂数据。但是若熵很大，子集比较小，这种情况没有前者糟糕。因此这个标准一定要兼顾到熵值和子集大小。

可以使用加权平均值来衡量，“权”表示子集在全部示例中的占有比例。然后选出最小的那个模型即可。

但是实际当中，我们也会计算根节点的熵值，然后用根节点熵值减去分裂后加权平均熵值，使用这个差值来计划选择哪个特征。

我们刚刚计算的这些数字，0.28、0.03.和0.12这些被称为信息增益，衡量的是由于分裂而导致的树中熵的减少。

为什么我们不直接使用加权平均熵来衡量，而是使用更费劲的差值呢？这是因为，熵减小的程度可以用来度量何时停止分裂。如果差值太小，小于某种阈值，可以判断此时停止分裂。

1.4.1 信息增益的一般公式

如下图所示：

二、决策树的优化

4.1 独热编码one-hot

前面的示例中，耳朵形状特征只有两个 ---尖的、圆的。如果我们增加一个取值，即尖的、圆的、椭圆的。此时根据耳朵形状分裂就会变成下图所示：

这会导致决策树变复杂。现在有一种方法one-hot来解决两个以上值的特征问题。我们删除耳朵形状这个特征，而是换成以下三个二值特征：是否是尖耳朵、是否是圆耳朵、是否是椭圆耳朵。如下图所示：

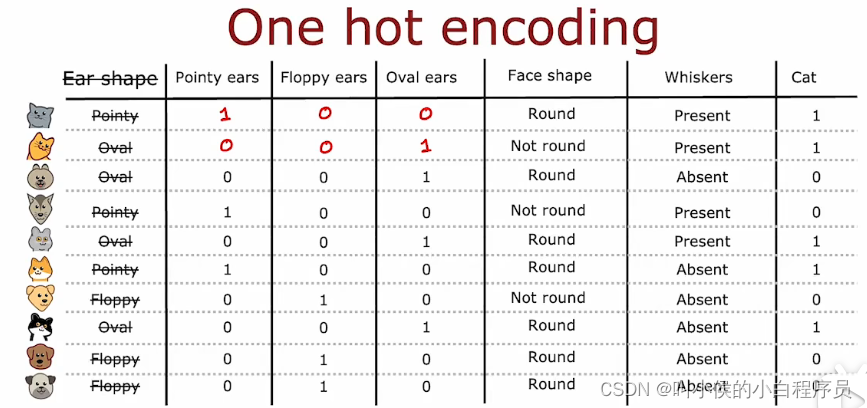
4.2 连续值特征

如果我们在特征中增加一个新的特征weight（体重），如下图所示，这个特征的取值无穷多，可以说是连续值特征。对于这样的特征该怎么处理呢？

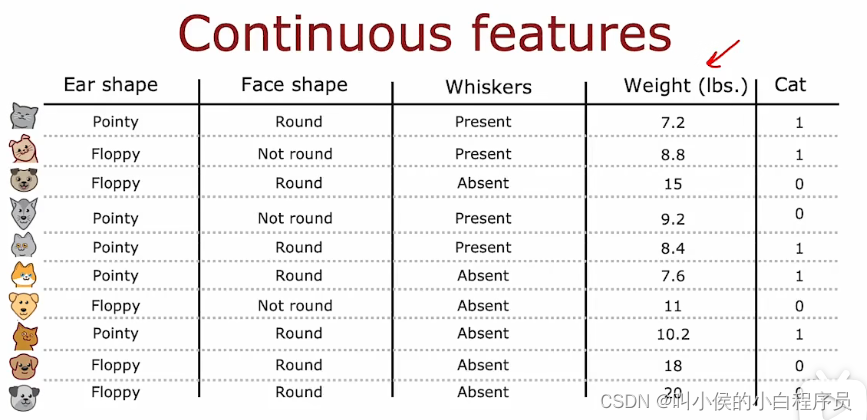
如下图所示，横轴是体重值，纵轴y=1表示是猫，y=0表示不是猫。我们可以设置不同的体重阈值来进行分裂。例如当阈值为8时，将体重小于等于8的分裂为一个子集，体重大于8的分裂为另一个子集。然后计算这个分裂标准的信息增益来判断这个阈值是否合理。我们可以设置多个不同的阈值来进行判断，如下图所示，分别设置了阈值为8，9，13，分别计算信息增益，由此可以看出，阈值为9的效果最好。

三、回归树

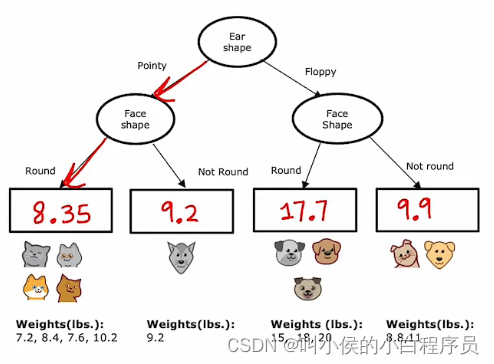
现在我们把问题换成下图所示，用耳朵形状、面部形状、胡须这三个特征来预测体重。

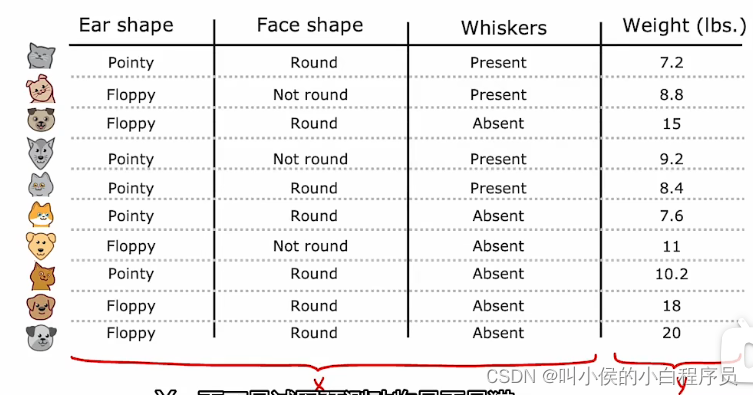
下图是构建的回归树，叶节点的值是分裂子集的体重的平均值。当测试新数据时，让他像往常一样往下走，当走到叶节点的时候，用平均值来预测新测试数据的weight。

3.1 选择最佳特征

如同决策树，在根节点有三个特征允许选择进行分裂，如下图所示，那么如何评价三种分裂方式的好坏呢？

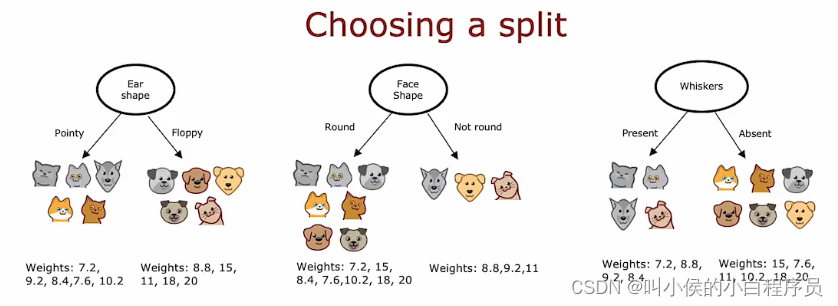
在构建回归树时，我们不是试图减少熵（对分类问题的杂质度量），而是尝试减少每个数据子集的值Y的权重方差。我们计算左右分支的方差，然后求取加权平均值，最后选出最小的那个模型即可。

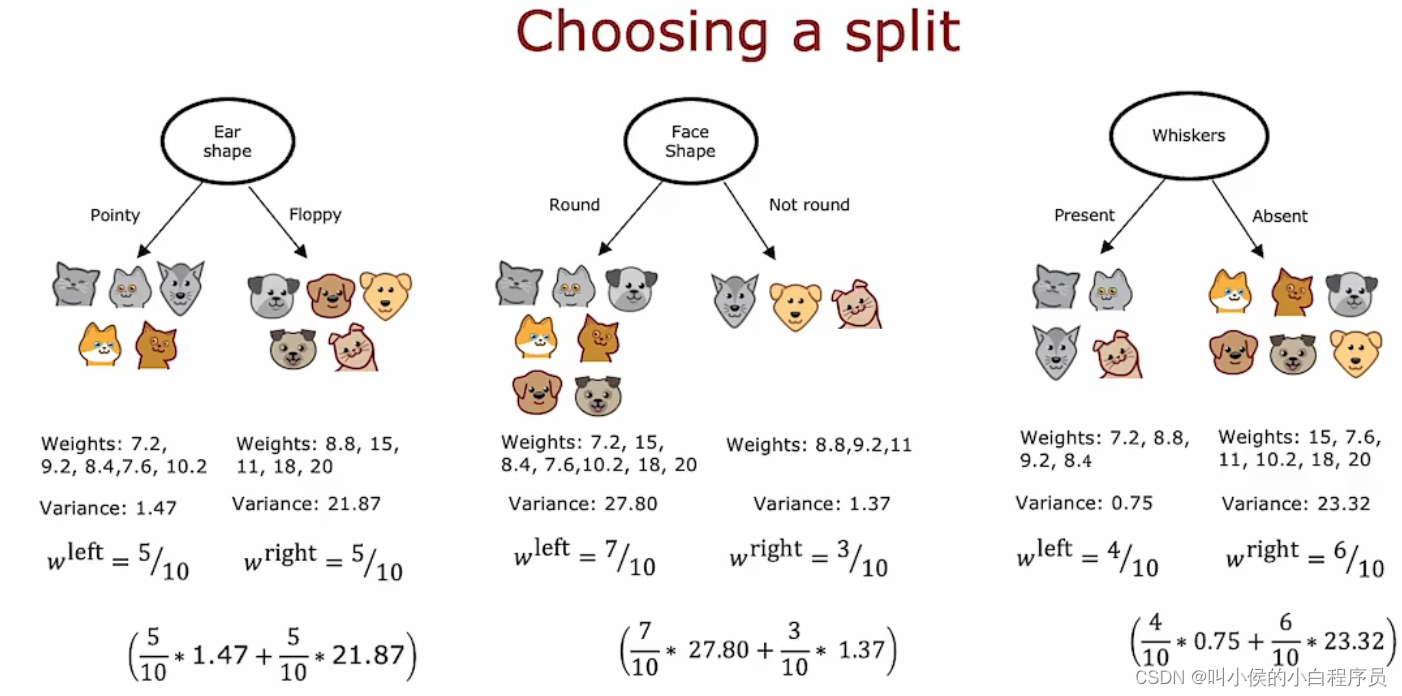
同决策树一样，我们也可以计算根节点的方差，然后用根节点方差减去分裂后加权平均方差，选择可以使方差最大程度减少的模型。

四、决策树集成

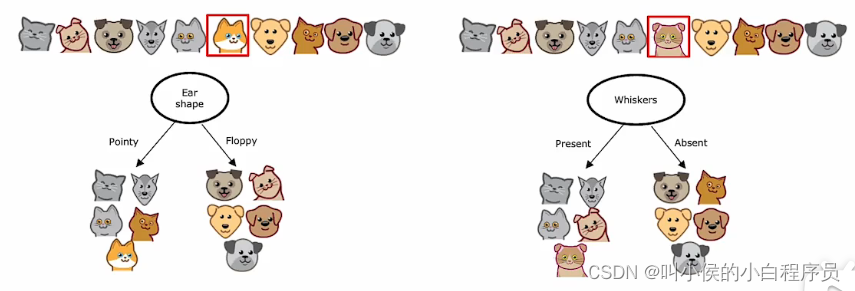
使用单个决策树的缺点之一是该决策树可能对数据中的微小变化高度敏感，如下图所示。左边是针对数据做出的最佳分裂模型，右边是仅仅更改一个数据后做出的最佳模型。10个测试数据只更改了一个，造成两个决策树完全不一样。

一种解决方案是不构建一个决策树，而是构建很多决策树，我们称之为树集成，如下图所示。当有一个新的测试数据，我们将这个数据在三个决策树上都跑一遍，每个决策树都会给出一个预测结果。这些结果相当于投票，哪个票数最多，最终就预测哪个。比如说，这里的三颗决策树，两个预测是猫，那么最终结果就是猫。

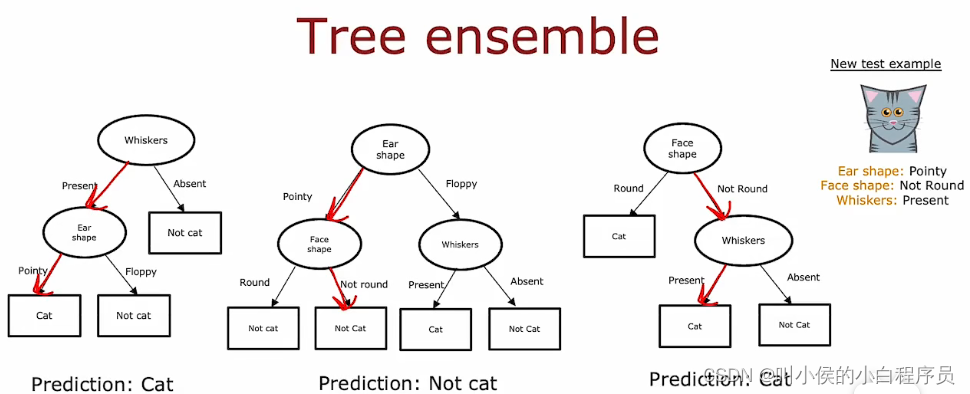
我们使用树集合的原因是通过拥有大量决策树并让它们投票，它使整体算法对任何一棵树可能正在做的事情不太敏感，因为它只能获得三分之一的投票，可以使整体算法更加健壮。

4.1 替换采样

如何构建决策树集合呢？可以使用替换采样的方法。替换采样的意思就是，从训练数据（数量为M）中随机抽取一个记录下来，把这个数据再放回去，再进行随机抽取。。。。。直到达到M个数据集（可能有重复的数据，不过这都是正常的）。这样是第一个数据集，利用这个数据集构建第一个决策树。然后用同样的方法，构建第二、第三等决策树。

构建决策树集合时，假设构建B棵决策树。事实证明将B设置得更大不会损害性能，但超过某个点后，最终会得到收益递减的结果，而且当B远大于1000左右时，它实际上并没有变得更好。

4.2 随机森林

即使使用这种带有替换过程的采样，有时最终还是会在根节点处始终使用相同的拆分，而在其余分裂节点附近使用非常相似的拆分。这种情况在小样示例中不明显，但是训练数据大的情况下会比较严重。因此，需要对算法再进行一次修改，以进一步尝试随机化每个分裂节点的特征选择，这会使树集彼此之间变得更加不同，这样的话，当您投票给他们时，您最终会得到更准确的预测。

通常这样做的方法是在每个分裂节点上选择一个特征以用于切割 (如果最终特征可用)。选择K个特征作为允许的特征，然后从这K个特征中选择具有最高信息增益的特征作为使用分割的特征选择。K 值的典型选择是 N的平方根，这种技术往往更多地用于具有大量特征的较大问题。注意k是从N个特征中随机抽取的。

4.3 XGBoost

在4.1中，构建决策树集成时，每次都从测试数据中，等概率（1/M的概率大小）抽取M个数据来构建决策树。XGBoost算法在此基础上继续改进，除了第一棵决策树和之前一样之外，剩余决策树都不是等概率抽取数据，而是更大概率能选择先前训练的树表现不佳的错误分类样本（这种方法称为“刻意练习”）。事实证明它可以帮助学习算法更快地学习，做得更好。因为后面的决策树把学习的重点放在了错误分类的数据上。

下图是第一棵决策树的构建，构建成功之后，对原始训练数据进行第一次预测，如下图红框的表格。我们在这个循环中第二次要做的是使用替换采样来生成另一个包含十个例子的训练集。但是每次我们从这10个中选择一个示例时，都会有更高的机会从这三个错误分类的示例中选择。