目录
- 1. 主体思想
- 2. 算法流程
- 3. 代码实践
1. 主体思想
主成分分析(Principal Component Analysis)常用于实现数据降维,它通过线性变换将高维数据映射到低维空间,使得映射后的数据具有最大的方差。主成分可以理解成数据集中的特征,具体来说,第一主成分是数据中方差最大的特征(即该特征下的值的方差最大),数据点在该方向有最大的扩散性(即在该方向上包含的信息量最多)。第二主成分与第一主成分正交(即与第一主成分无关),并在所有可能正交方向中,选择方差次大的方向。然后,第三主成分与前两个主成分正交,且选择在其余所有可能正交方向中有最大方差的方向,以此类推,有多少特征就有多少主成分。
- 主成分上的方差越小,说明该特征上的取值可能都相同,那这一个特征的取值对样本而言就没有意义,因为其包含的信息量较少。
- 主成分上的方差越大,说明该特征上的值越分散,那么它包含的信息就越多,对数据降维就越有帮助。
下图1中,紫色线方向上数据的方差最大(该方向上点的分布最分散,包含了更多的信息量),则可以将该方向上的特征作为第一主成分。

主成分分析的优点2:
- 数据降维:PCA能够减少数据的维度(复杂度),提高计算效率。
- 数据可视化:通过PCA降维,可以将数据可视化到更低维度的空间中,便于数据的观察和理解。
- 去除噪声: 主成分分析可以把数据的主要特征提取出来(数据的主要特征集中在少数几个主成分上),忽略小的、可能是噪声的特征,同时可以防止过拟合。
- 去除冗余: 在原始数据中,很多情况下多个变量之间存在高度相关性,导致数据冗余。PCA通过新的一组正交的主成分来描述数据,可以最大程度降低原始的数据冗余。
2. 算法流程
- 数据预处理:中心化 x i − x ˉ x_i-\bar{x} xi−xˉ (每列的每个值都减去该列的均值)。
- 求样本的协方差矩阵 1 m X T X \frac{1}{m}X^TX m1XTX(m为样本数量,X为样本矩阵)。
- 计算协方差矩阵的特征值和对应的特征向量。
- 选择最大的 K K K 个特征值对应的 K K K 个特征向量构造特征矩阵。
- 将中心化后的数据投影到特征矩阵上。
- 输出投影后的数据集。
协方差矩阵的计算(二维)
C = 1 m X T X = ( C o v ( x , x ) C o v ( x , y ) C o v ( y , x ) C o v ( y , y ) ) = ( 1 m ∑ i = 1 m x i 2 1 m ∑ i = 1 m x i y i 1 m ∑ i = 1 m y i x i 1 m ∑ i = 1 m y i 2 ) C=\frac{1}{m}X^TX=\begin{pmatrix}Cov(x,x)&Cov(x,y) \\Cov(y,x)&Cov(y,y)\end{pmatrix} =\begin{pmatrix} \frac{1}{m}\sum_{i=1}^{m}x_i^2&\frac{1}{m}\sum_{i=1}^{m}x_iy_i \\ \frac{1}{m}\sum_{i=1}^{m}y_ix_i&\frac{1}{m}\sum_{i=1}^{m}y_i^2 \end{pmatrix} C=m1XTX=(Cov(x,x)Cov(y,x)Cov(x,y)Cov(y,y))=(m1∑i=1mxi2m1∑i=1myixim1∑i=1mxiyim1∑i=1myi2)
其中, x x x 和 y y y 表示不同的特征列, c o v ( x , x ) = D ( x ) = 1 m ∑ i = 1 m ( x i − x ˉ ) 2 cov(x,x)=D(x)=\frac{1}{m}\sum_{i=1}^{m}(x_i-\bar{x})^2 cov(x,x)=D(x)=m1∑i=1m(xi−xˉ)2(协方差矩阵中的 x i x_i xi 表示已经中心化后的值),协方差矩阵是一个对称的矩阵,且对角线元素是各个特征(一列即为一个特征)的方差。
协方差矩阵的计算(三维)
C = ( C o v ( x , x ) C o v ( x , y ) C o v ( x , z ) C o v ( y , x ) C o v ( y , y ) C o v ( y , z ) C o v ( z , x ) C o v ( z , y ) C o v ( z , z ) ) C=\begin{pmatrix} Cov(x,x)&Cov(x,y)&Cov(x,z) \\ Cov(y,x)&Cov(y,y)&Cov(y,z) \\ Cov(z,x)&Cov(z,y)&Cov(z,z) \end{pmatrix} C= Cov(x,x)Cov(y,x)Cov(z,x)Cov(x,y)Cov(y,y)Cov(z,y)Cov(x,z)Cov(y,z)Cov(z,z)
举例说明
下面共5个样本,每个样本两个特征,第一列的均值为2.2,第二列的均值为3.8。
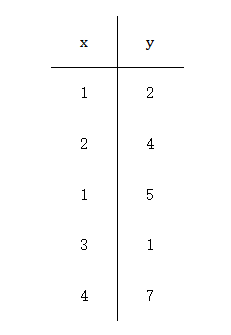
-
数据中心化(每列的每个值都减去该列的均值)

-
计算协方差矩阵
C = [ 1.7 1.05 1.05 5.7 ] C=\begin{bmatrix} 1.7&1.05 \\ 1.05&5.7 \end{bmatrix} C=[1.71.051.055.7] -
计算特征值与特征向量
e i g e n v a l u e s = [ 1.4411286 , 5.9588714 ] eigenvalues=[1.4411286,5.9588714] eigenvalues=[1.4411286,5.9588714]
e i g e n v e c t o r s = [ − 0.97092685 − 0.23937637 0.23937637 − 0.97092685 ] eigenvectors=\begin{bmatrix} -0.97092685&-0.23937637\\ 0.23937637&-0.97092685 \end{bmatrix} eigenvectors=[−0.970926850.23937637−0.23937637−0.97092685] -
选择最大的一个特征值(将数据降为一维)5.9588714,对应的特征向量为
[ − 0.23937637 − 0.97092685 ] \begin{bmatrix} -0.23937637\\ -0.97092685 \end{bmatrix} [−0.23937637−0.97092685] -
将中心化后的数据投影到特征矩阵
[ − 1.2 − 1.8 − 0.2 0.2 − 1.2 1.2 0.8 − 2.8 1.8 3.2 ] ∗ [ − 0.23937637 − 0.97092685 ] = [ 2.03491998 − 0.1463101 − 0.87786057 2.52709409 − 3.5378434 ] \begin{bmatrix} -1.2&-1.8 \\ -0.2&0.2 \\ -1.2&1.2 \\ 0.8&-2.8 \\ 1.8&3.2 \end{bmatrix}*\begin{bmatrix} -0.23937637\\ -0.97092685 \end{bmatrix}=\begin{bmatrix} 2.03491998\\ -0.1463101\\ -0.87786057\\ 2.52709409\\ -3.5378434 \end{bmatrix} −1.2−0.2−1.20.81.8−1.80.21.2−2.83.2 ∗[−0.23937637−0.97092685]= 2.03491998−0.1463101−0.877860572.52709409−3.5378434
[ 2.03491998 − 0.1463101 − 0.87786057 2.52709409 − 3.5378434 ] \begin{bmatrix} 2.03491998\\ -0.1463101\\ -0.87786057\\ 2.52709409\\ -3.5378434 \end{bmatrix} 2.03491998−0.1463101−0.877860572.52709409−3.5378434 即为降维后的数据。
3. 代码实践
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
import numpy as np
import matplotlib.pyplot as plt# 载入手写体数据集并切分为训练集和测试集
digits = load_digits()
x_data = digits.data
y_data = digits.target
x_train, x_test, y_train, y_test = train_test_split(x_data,y_data)
x_data.shape
运行结果
(1797, 64)
# 创建神经网络模型,包含两个隐藏层,每个隐藏层的神经元数量分别为
# 100和50,最大迭代次数为500
mlp = MLPClassifier(hidden_layer_sizes=(100,50) ,max_iter=500)
mlp.fit(x_train,y_train)
# 数据中心化
def zeroMean(dataMat):# 按列求平均,即各个特征的平均meanVal = np.mean(dataMat, axis=0) newData = dataMat - meanValreturn newData, meanVal# PCA降维,top表示要将数据降维到几维
def pca(dataMat,top):# 数据中心化newData,meanVal=zeroMean(dataMat) # np.cov用于求协方差矩阵,参数rowvar=0说明数据一行代表一个样本covMat = np.cov(newData, rowvar=0)# np.linalg.eig求矩阵的特征值和特征向量eigVals, eigVects = np.linalg.eig(np.mat(covMat))# 对特征值从小到大排序eigValIndice = np.argsort(eigVals)# 从eigValIndice中提取倒数top个索引,并按照从大到小的顺序返回一个切片列表# 后一个 -1 表示切片的方向为从后往前,以负的步长(-1)进行迭代n_eigValIndice = eigValIndice[-1:-(top+1):-1]# 最大的n个特征值对应的特征向量n_eigVect = eigVects[:,n_eigValIndice]# 低维特征空间的数据lowDDataMat = newData*n_eigVect# 利用低纬度数据来重构数据reconMat = (lowDDataMat*n_eigVect.T) + meanVal# 返回低维特征空间的数据和重构的矩阵return lowDDataMat,reconMat
# 绘制降维后的数据及分类结果,共10个类
lowDDataMat, reconMat = pca(x_data, 2)
predictions = mlp.predict(x_data)
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
plt.scatter(x,y,c=y_data)
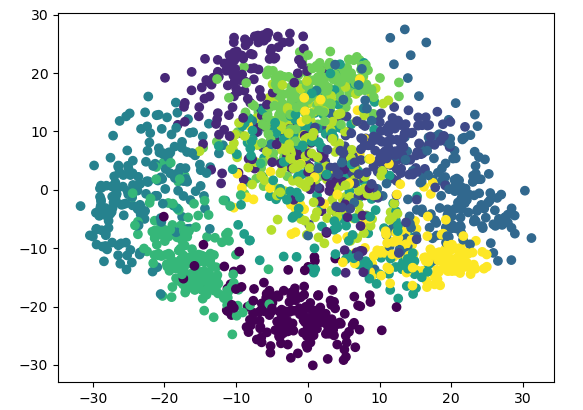
# 将数据降为3维
lowDDataMat, reconMat = pca(x_data,3)
# 绘制三维数据及分类结果,共10个类
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
z = np.array(lowDDataMat)[:,2]
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x, y, z, c = y_data, s = 10) #点为红色三角形
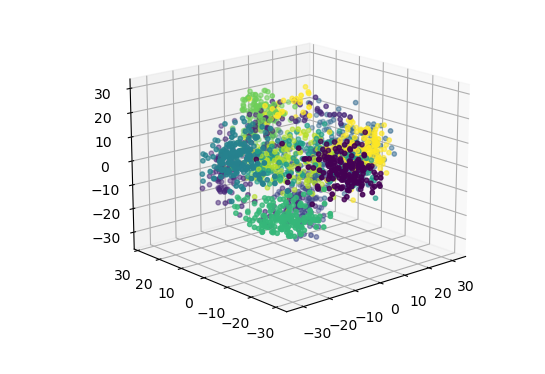
主成分分析(PCA) ↩︎
主成分分析(PCA)理解 ↩︎



。Javaee项目,ssm vue前后端分离项目。)
(二))


)



 PostgreSQL 14 15 16)
)

)




