1.前序遍历

1.1思路

其实对于二叉树的非递归实现，实际上就是用代码来模拟操作系统压栈和弹栈的过程。让我们一起来看看吧，首先将一棵树分为左边节点和左边节点的右子树。如图：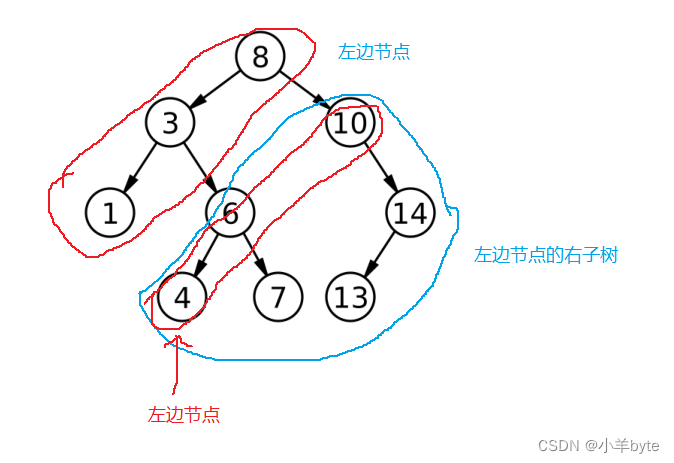

然后借助于一个栈，先将左边节点入栈，入栈时要将节点的值存到数组中。将左边节点全部入栈后，再来将左边节点的右子树入栈，重复上述过程。直至栈为空并且，当前的指针也为空，此时完成二叉树的前序遍历。如图：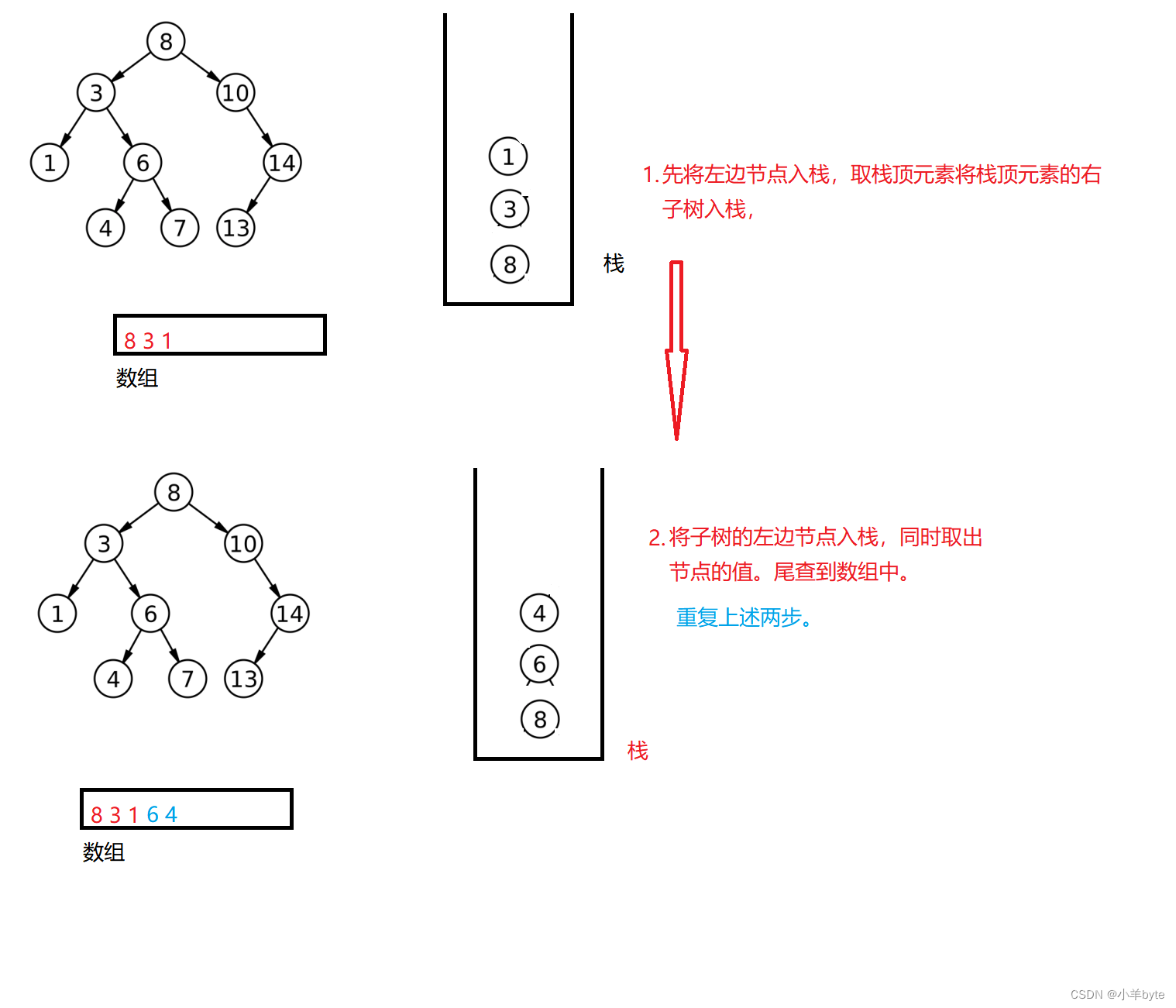

1.2代码实现

    vector<int> preorderTraversal(TreeNode* root){vector<int> v;stack<TreeNode*> sT;//1.处理左边节点//2.处理左边节点的右子树TreeNode * cur = root;while(cur ||  !sT.empty()  ){while(cur){//左边节点入栈sT.push(cur);v.push_back(cur->val);cur = cur -> left;}TreeNode* p = sT.top();sT.pop();cur = p -> right;//左边节点的右子树入栈}return v;}

2.中序遍历

2.1思路

中序遍历的思路和前序遍历基本相同，就是此时左边节点入栈时不会将左边节点的val插到数组中，而是在栈中将节点的指针取出时再尾插到数组中。

2.2代码实现

  vector<int> inorderTraversal(TreeNode* root) {vector<int> ret;stack< TreeNode* > sT;TreeNode* cur = root;while(cur || !sT.empty()){//树的左边节点入栈while(cur){sT.push(cur);cur = cur -> left;}//取出栈顶节点的指针//将栈顶节点指针的val尾插到数组中TreeNode * top = sT.top();sT.pop();//左边节点的右子树入栈cur = top -> right;ret.push_back(top->val);}return ret;}

3.后序遍历

3.1思路

后序遍历沿用了中序遍历的思路，唯一不同的是将左边节点依次入栈后，出栈时先处理当前节点的左子树，然后将右子树入栈，等处理完右子树后再来处理当前节点。

3.2代码实现

vector<int> postorderTraversal(TreeNode* root) {TreeNode * cur = root;TreeNode * back = nullptr;//用来记录处理上一个节点vector<int> ret;stack<TreeNode*> sT;while(cur || !sT.empty() ){//左边节点入栈while(cur){sT.push(cur);cur = cur->left;}//取出栈顶数据TreeNode* top = sT.top();if(top->right == nullptr || top->right == back){ret.push_back(top->val);back = top;//记录处理过的节点sT.pop();}else{//左边节点的右子树入栈cur = top -> right;}}return ret;}

后续遍历需要注意的是在什么时候来对当前节点进行处理，要先处理左右节点之后对当前节点进行处理，如果右节点为空很好办直接判断右节点为不为空就可以了，但是如果右节点不为空呢？怎么确保右节点已经处理过了再来对当前节点进行处理呢，这里提供一种较为简单的思路，通过一个指针来记录上次处理的节点，因为后序遍历总是按照左子树，右子树和根的处理顺序来的所以我们只需要处理比较上一个处理的节点是不是当前节点的右子树就可以知道当前节点的右子树是否已经被处理过了，来判断当前节点是否需要处理。

讲的不好，希望不要喷我。