介绍一种可视化feaature maps以及kernel weights的方法
推荐可视化工具TensorBoard:可以查看整个计算图的数据流向,保存再训练过程中的损失信息,准确率信息等
学习视频:
使用pytorch查看中间层特征矩阵以及卷积核参数_哔哩哔哩_bilibili
代码下载:
deep-learning-for-image-processing/pytorch_classification/analyze_weights_featuremap at master · WZMIAOMIAO/deep-learning-for-image-processing · GitHub
一、所需文件
AlexNet.pth 和 resNet34.pth 文件通过之前的训练获得
二、操作步骤
AlexNet 的中间层特征矩阵
1.在analyze_feature_map.py 文件的 out_put 处设置断点并debug,查看print model所打印的信息
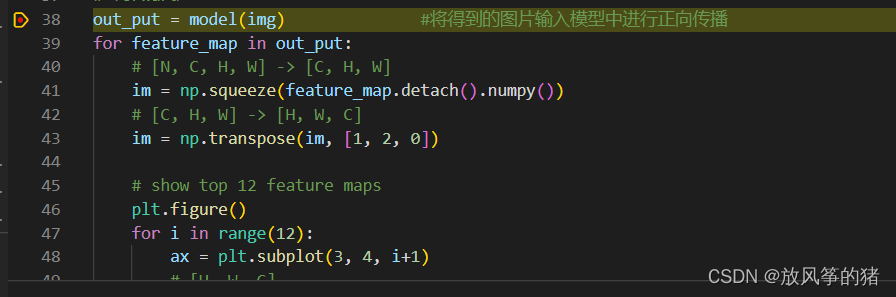
- 打印两个层结构:第一个是features,第二个是classifier,与 alexnet_model.py文件中的所定义的层结构一一对应,如下图所示:
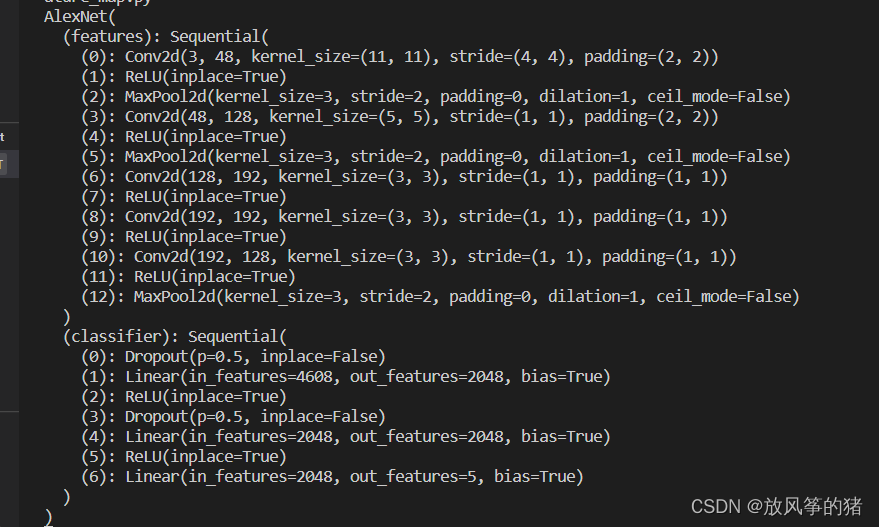
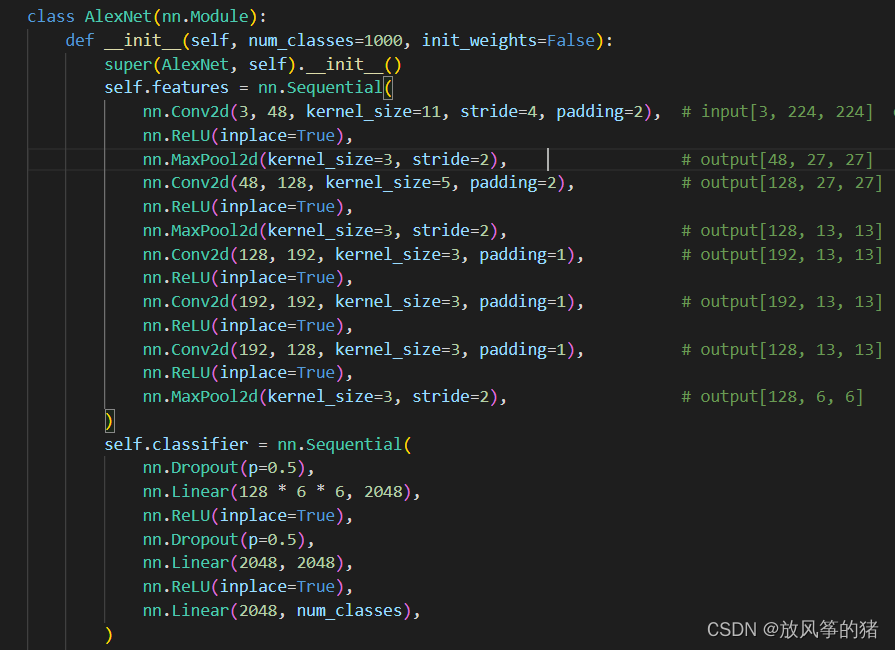
- 在 alexnet_model.py 文件的 for name, module in self.features.named_children(): 行设置断点并单步运行
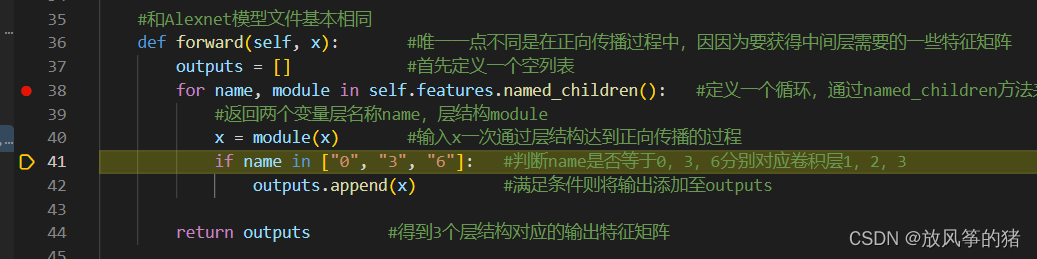
得到name = 0 和卷积层conv 2d,后面以此类推
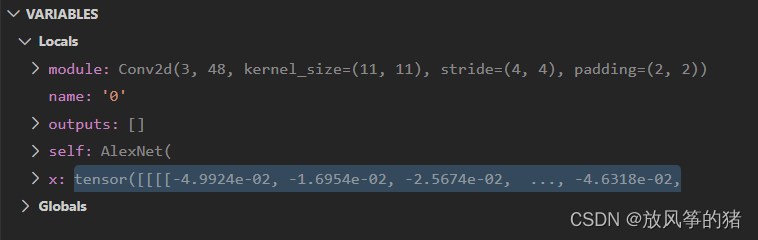
- 让程序接着运行到for循环处
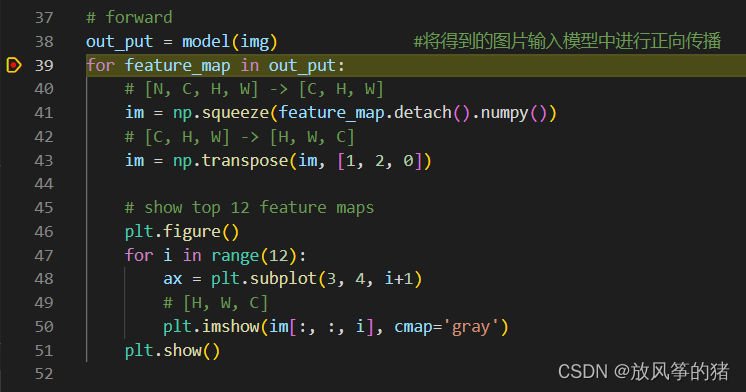
查看out_put,是一个list,一共有三层,分别对应第一个,第二个,第三个卷积层的输出特征矩阵

5.让程序执行完
(1)输出为第一个卷积层 所输出的特征矩阵的前12个通道的特征图
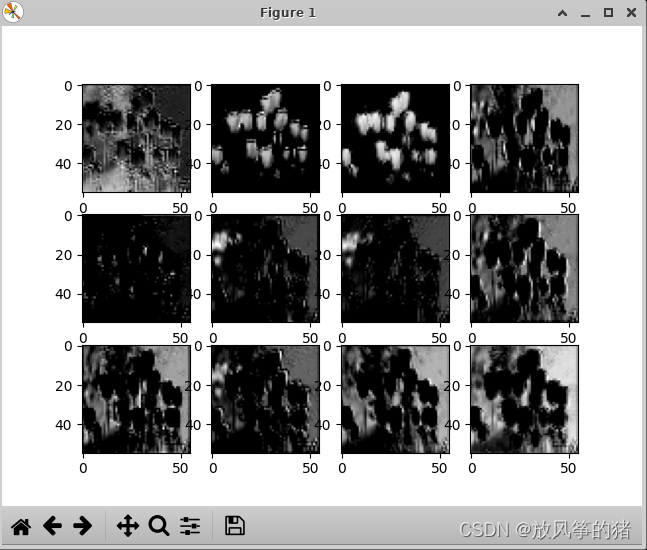
通过特征图的明暗程度来理解卷积层一所关注的一些信息,亮度越高的地方就是卷积层越感兴趣的地方。
原图如下:

(2)卷积层二所输出的特征矩阵:抽象程度越来越高,有些卷积核没有起到作用
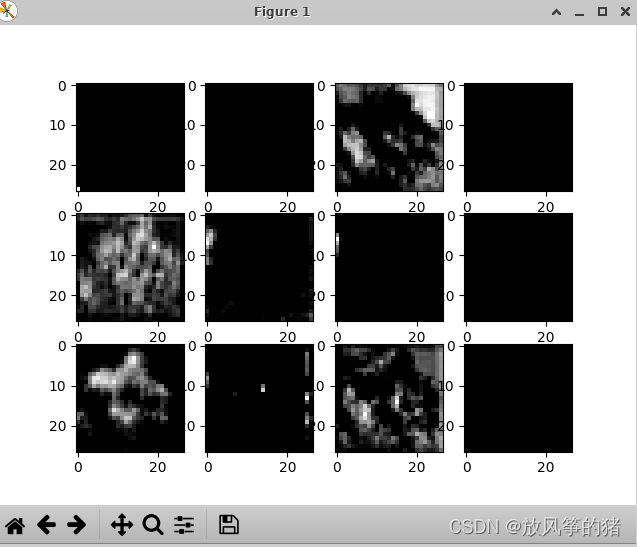
卷积层三 所输出的特征矩阵
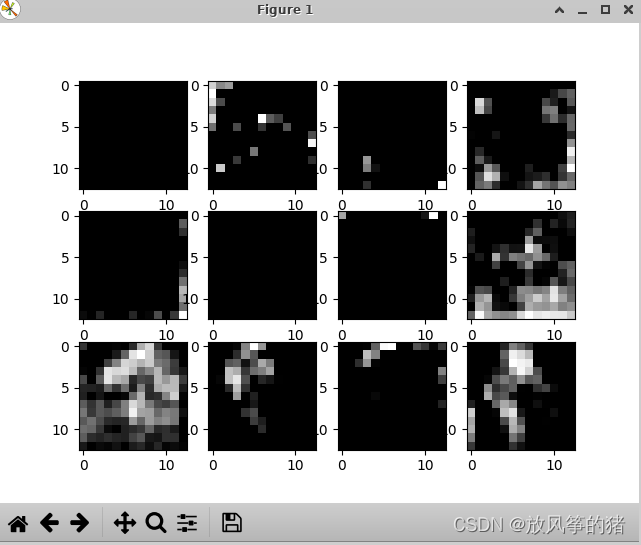
(3)去掉cmap='gray’之后的颜色为蓝绿色
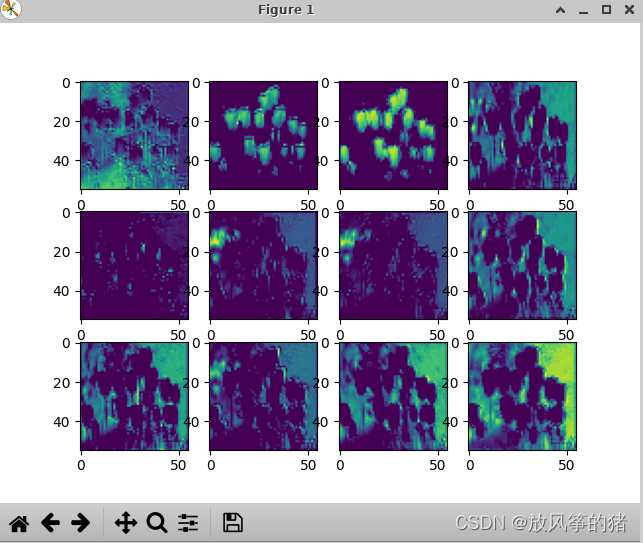
(4)如果想看更多信息,则在 alexnet_model.py 的向前传播过程中进行修改
假如要看全连接层的图像,则也要将输入的图像通过features层结构,再通过全连接层才能查看
resnet34 的中间层特征矩阵
1.修改代码并再下图处设置断点debug
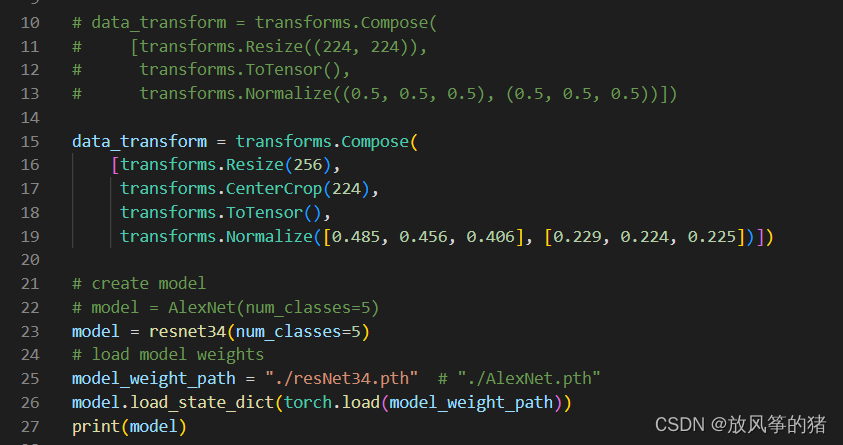
可以再终端看到resnet的层结构
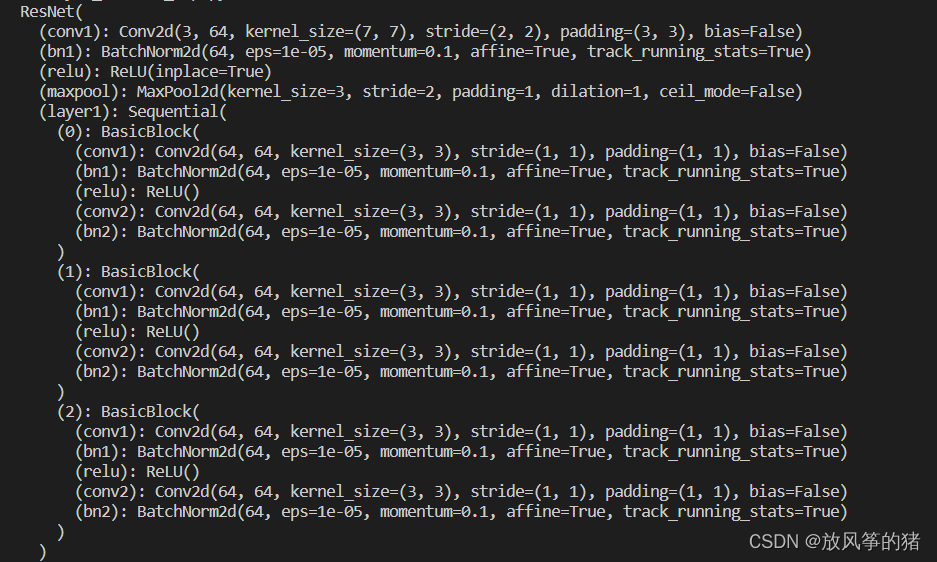
2.运行结果如图
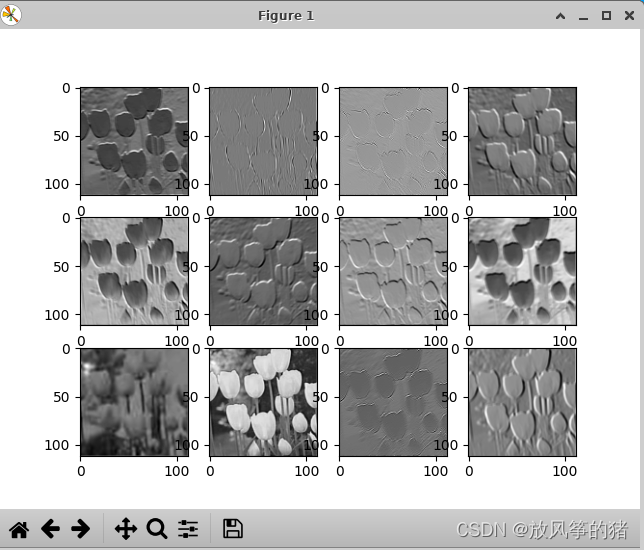
明显resnet学习到的信息比 alexnet更多
有两个原因:resnet确实比alexnet更加优秀
resnet使用迁移学习的方法,并且预训练数据集是使用 imagenet 数据集进行训练的
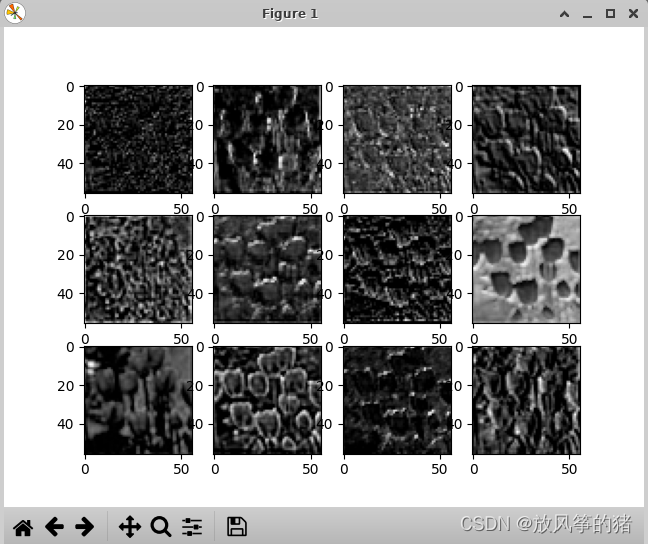
3.layer1所输出的特征矩阵,明显比alexnet好很多,每一个特征层都有输出,都是有用的
AlexNet 的卷积核参数
- 打开 analyze_kernel_weight.py 文件

这里可以不用实例化模型,直接通过 torch.load 函数载入训练权重,因为通过 torch.load 载入后,就是一个字典类型,它的key就代表每个层结构的名称,对应的value就是每层的训练信息
- 通过 model.state_dict 函数获取模型中所有的可训练参数的字典,再通过keys方法获取所有的具有参数的层结构的名称
单步运行看一下weights_keys
如下图所示,weights_keys 是一个有序的keys,按照正向传播过程的顺序进行保存的
命名规则:
feature0,feature3,feature6,feature8,feature10等卷积层才有训练参数
激活函数和最大池化下采样是没有激活函数的

3.接下来遍历 weights_keys
model.state_dict 函数获取模型中所有的可训练参数的字典信息,传入对应的key就得到了参数信息,再通过numpy方法将权值信息转化为numpy格式,方便分析
注意:卷积核通道的排列顺序是
kernel_number 卷积核个数,对应的输出特征矩阵的深度
kernel_channel 卷积核深度,对应的输入特征矩阵的深度
kernel_height, kernel_width,卷积核的高度和宽度
- 获得信息
# k = weight_t[0, :, :, :] # 通过切片的方式获得信息# calculate mean, std, min, max 对所有卷积核的信息进行计算weight_mean = weight_t.mean() #均值weight_std = weight_t.std(ddof=1) #标准差weight_min = weight_t.min() #最小值weight_max = weight_t.max() #最大值
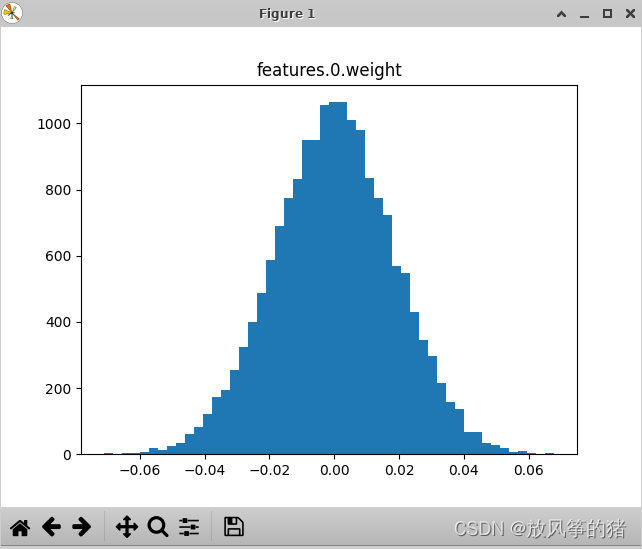
卷积层一对应的卷积核值的分布
卷积层一对应的偏置的分布
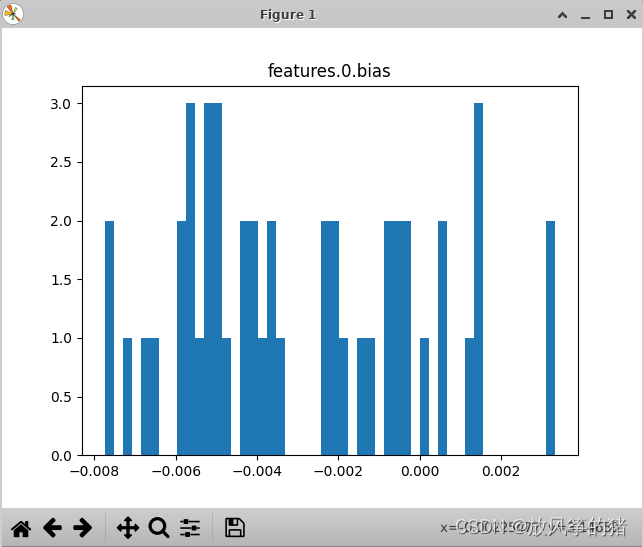
后面的都是一样的,不做展示
ResNet 的卷积核参数
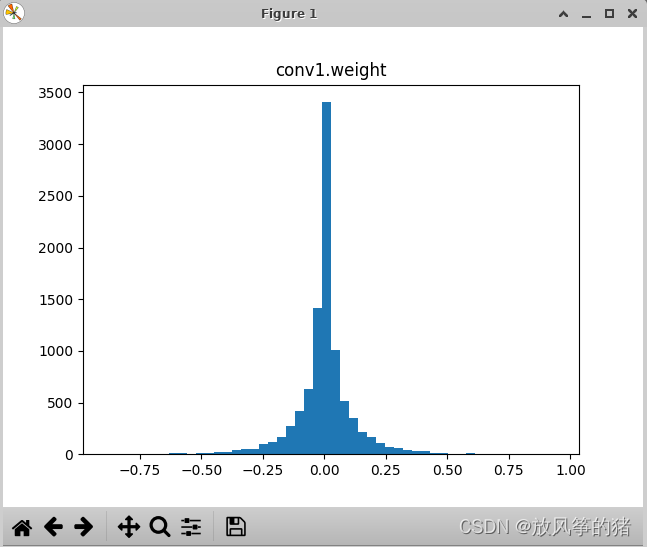
1.第一个卷积层的分布
2.bn层的分布,使用bn时就不用使用偏置
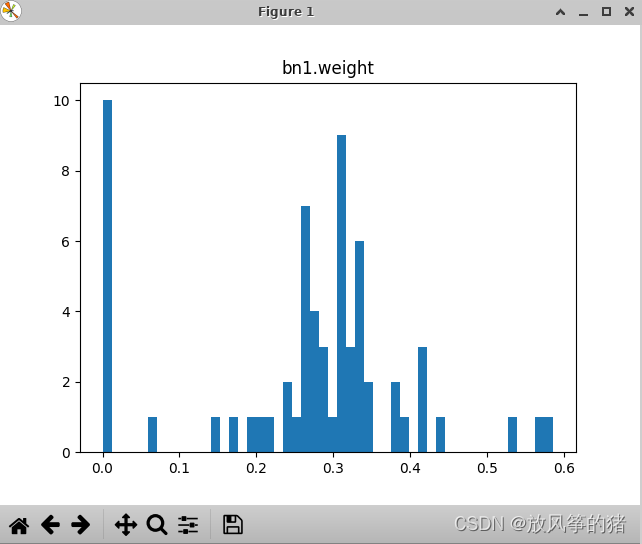
weight就是下图的 参数

bias对应上图的 参数
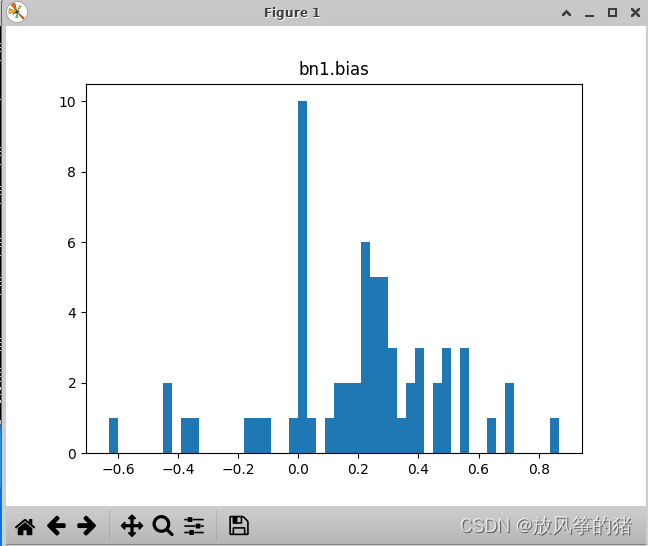
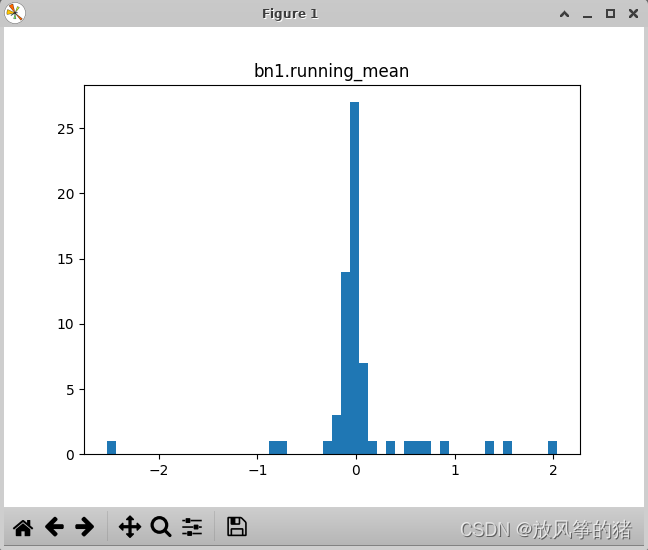
mean对应的是均值 ,是统计得到的
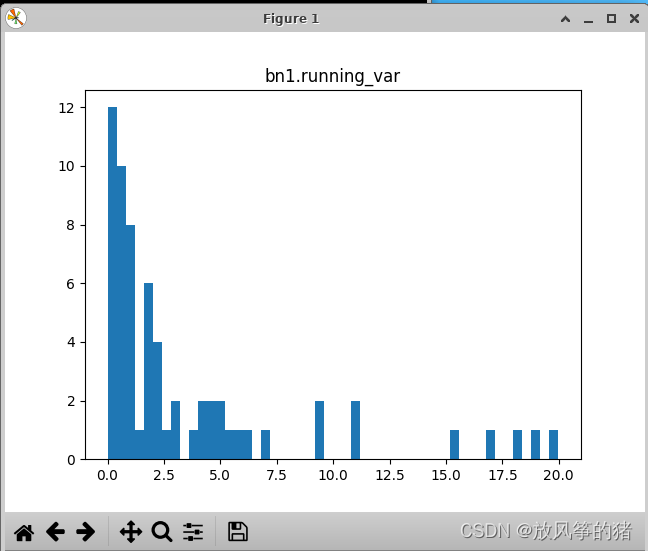
方差 也是统计得到的
后面的输出都是一样的结构。


----c++)

)






![[网鼎杯 2020 朱雀组]Nmap](http://pic.xiahunao.cn/[网鼎杯 2020 朱雀组]Nmap)

)

)


)
)