激活函数是神经网络中的重要组成部分,有力地推动了深度学习的发展。然而,仅仅了解和选择激活函数是不够的,我们还需要理解激活函数的导数。本文将详细介绍激活函数的概念、作用及其导数的重要性,并探究导数对神经网络训练的影响。
第一节:激活函数的概念和作用
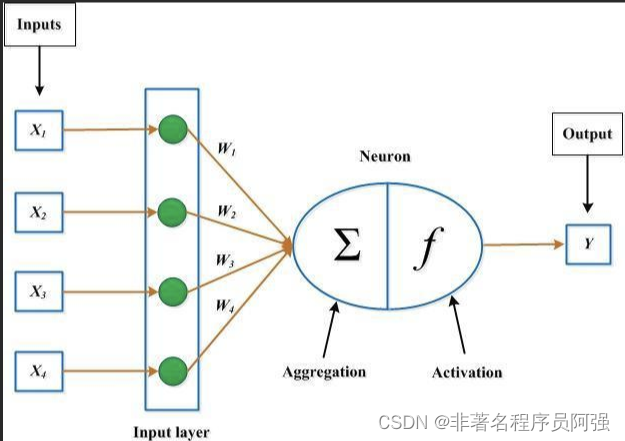
激活函数是神经元中常用的非线性映射函数,它将输入信号转化为输出信号。激活函数的作用是引入非线性性质,从而提升神经网络的表达能力。通过选择适当的激活函数,我们可以实现非线性决策边界,并更好地处理实际问题中的非线性数据。
第二节:常见的激活函数及其图像
1. 阶跃函数(Step Function):阶跃函数是最简单的激活函数之一,它在输入小于等于0时输出0,大于0时输出1。阶跃函数的导数几乎处处为零,因此不适合在反向传播中使用。
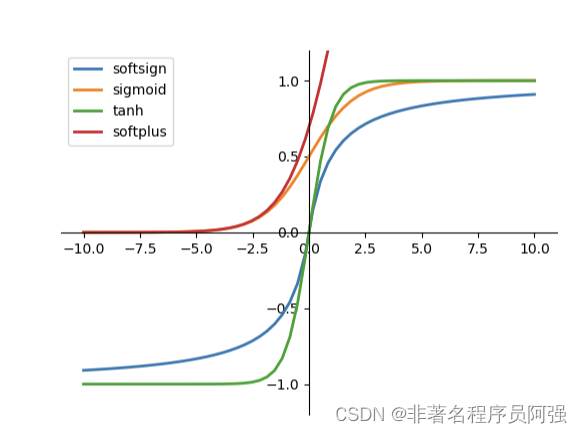
2. sigmoid函数(Sigmoid Function):sigmoid函数具有S形曲线,将输入映射到0到1之间的连续值。它的导数可以通过sigmoid函数本身来表示,有助于反向传播过程中梯度的计算。然而,当输入值远离0时,sigmoid函数的导数趋近于0,可能导致梯度消失的问题。
3. 双曲正切函数(Tanh Function):双曲正切函数与sigmoid函数类似,但其输出值范围是-1到1之间。双曲正切函数的导数在0附近比sigmoid函数的导数更大,这对于网络的训练有一定的优势。然而,它仍然存在导数趋近于0的问题。
4. ReLU函数(Rectified Linear Unit Function):ReLU函数是一种简单且广泛使用的激活函数,当输入大于0时输出输入值,否则输出0。ReLU函数的导数在输入大于0时恒为1,对于训练稳定性和梯度传播有很好的效果。但当输入小于等于0时,ReLU函数的导数为0,可能导致部分神经元“死亡”。
第三节:激活函数导数的重要性
激活函数导数在神经网络的训练中起着重要的作用:
1. 梯度计算:激活函数导数用于计算反向传播过程中的梯度。梯度可以指导我们调整网络的权重和偏置,以最小化损失函数并提升网络性能。
2. 梯度消失和梯度爆炸问题:激活函数导数的大小直接影响梯度传播的有效性。当激活函数导数趋近于0时,梯度在网络中传递时会逐渐减小,导致梯度消失问题;而当激活函数导数过大时,梯度可能会爆炸。因此,适当选择激活函数和对其导数进行控制非常重要。
3. 收敛速度和学习率:激活函数导数的大小也会影响网络的收敛速度和学习率的选择。合适的导数大小可以提高网络的学习速度和稳定性,有助于更快地达到收敛状态。
第四节:优化激活函数及其导数
为了克服激活函数导数的问题,研究者们提出了许多改进的激活函数,如Leaky ReLU、ELU和ReLU的变种等。这些函数在保留非线性性质的同时,改善了梯度消失和梯度爆炸等问题。
结论:
激活函数及其导数是神经网络中的关键元素,对网络的性能、训练稳定性和梯度传播起着至关重要的作用。了解不同激活函数的特点和导数的性质,能够帮助我们选择合适的激活函数,并优化网络的训练过程。进一步研究和改进激活函数及其导数,有助于推动神经网络领域的发展,并不断提升深度学习的能力和效果。
人工智能的学习之路非常漫长,不少人因为学习路线不对或者学习内容不够专业而举步难行。不过别担心,我为大家整理了一份600多G的学习资源,基本上涵盖了人工智能学习的所有内容。点击下方链接,0元进群领取学习资源,让你的学习之路更加顺畅!记得点赞、关注、收藏、转发哦!扫码进群领资料





:了解FFmpeg与SDL常用对象和函数)

校招面试真题解析,让你面试轻松无压力!)








)

)
