2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~共计18条视频，包括：2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~、第2讲 PyQt6库和工具库QTDesigner安装与配置、第3讲 PyQt6第一个程序HelloWorld实现等，UP主更多精彩视频，请关注UP账号。https://www.bilibili.com/video/BV11C4y1P7fj/

首先我们用QTDesigner设计一个简单UI。

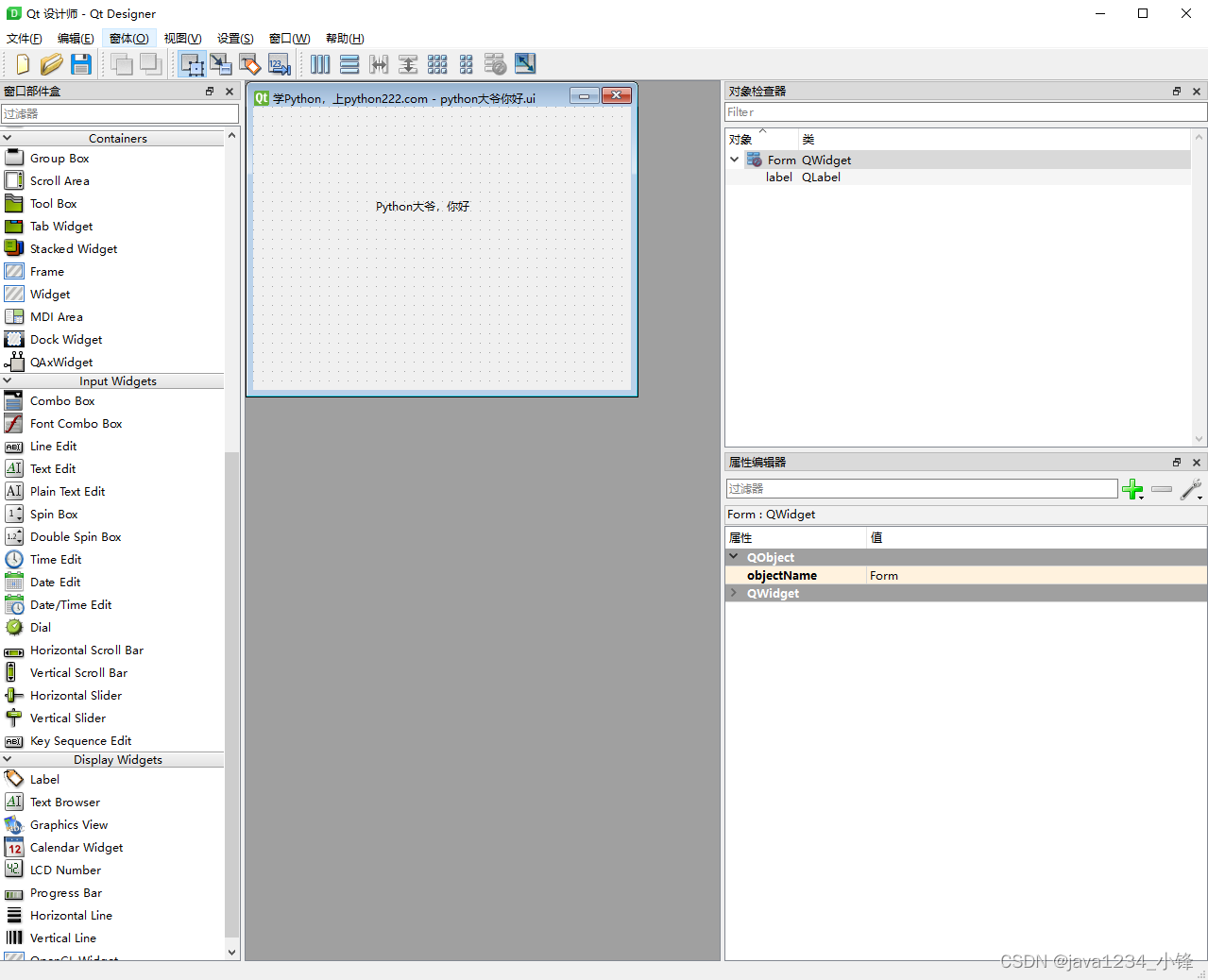
保存ui文件，放到项目里面去。

我们通过PyQt6包里面的uic来加载ui文件

"""python加载ui文件作者 : 小锋老师官网 : www.python222.com
"""
import sys
​
from PyQt6.QtWidgets import QApplication
from PyQt6 import uic
​
if __name__ == '__main__':app = QApplication(sys.argv)ui = uic.loadUi("./ui文件.ui")ui.show()
​sys.exit(app.exec())

后续我们会继续深入讲解，我们可以在当前代码里获取到ui文件里的所有控件，对控件属性以及行为进行设置操作。

以后标准开发，依然是建议通过这种界面与操作分离的方式进行项目开发，有利于分工明确，以及后期方便维护。