YOLOv8改进 | 2023 | LSKAttention大核注意力机制助力极限涨点

论文地址：官方论文地址

代码地址：官方代码地址

一、本文介绍 

在这篇文章中，我们将讲解如何将LSKAttention大核注意力机制应用于YOLOv8，以实现显著的性能提升。首先，我们介绍LSKAttention机制的基本原理，它主要通过将深度卷积层的2D卷积核分解为水平和垂直1D卷积核，减少了计算复杂性和内存占用。接着，我们介绍将这一机制整合到YOLOv8的方法，以及它如何帮助提高处理大型数据集和复杂视觉任务的效率和准确性。本文还将提供代码实现细节和使用方法，展示这种改进对目标检测、语义分割等方面的积极影响。通过实验YOLOv8在整合LSKAttention机制后，实现了检测精度提升(下面会附上改进LSKAttention机制和基础版本的结果对比图)。

 专栏回顾：YOLOv8改进系列专栏——本专栏持续复习各种顶会内容——科研必备

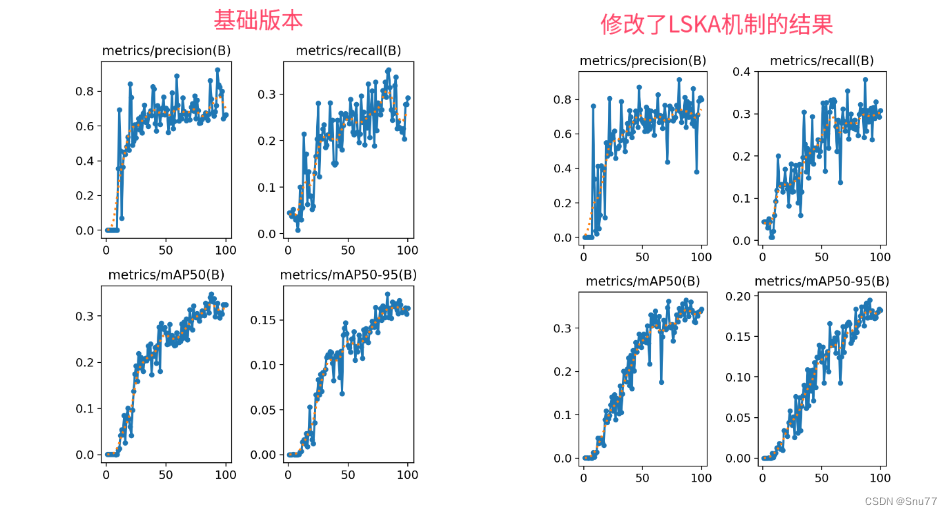
实验效果图如下所示-> 

本次实验我只用了一百张图片检测的是安全帽训练了一百个epoch，该结果只能展示出该机制有效，但是并不能产生决定性结果，因为具体的效果还要看你的数据集和实验环境所影响。

目录

一、本文介绍 

二、LSKAttention的机制原理 

三、LSKAttention的代码

四、手把手教你将LSKAttention添加到你的网络结构中

4.1 LSKAttention的添加教程

4.2 LSKAttention的yaml文件和训练截图

4.2.1 LSKAttention的yaml文件

4.2.2 LSKAttention的训练过程截图 

五、LSKAttention可添加的位置

5.1 推荐LSKAttention可添加的位置 

5.2图示LSKAttention可添加的位置 

六、本文总结 

二、LSKAttention的机制原理 

《Large Separable Kernel Attention》这篇论文提出的LSKAttention的机制原理是针对传统大核注意力（Large Kernel Attention，LKA）模块在视觉注意网络（Visual Attention Networks，VAN）中的应用问题进行的改进。LKA模块在处理大尺寸卷积核时面临着高计算和内存需求的挑战。LSKAttention通过以下几个关键步骤和原理来解决这些问题：

  1. 核分解：LSKAttention的核心创新是将传统的2D卷积核分解为两个1D卷积核。首先，它将一个大的2D核分解成水平（横向）和垂直（纵向）的两个1D核。这样的分解大幅降低了参数数量和计算复杂度。

  2. 串联卷积操作：在进行卷积操作时，LSKAttention首先使用一个1D核对输入进行水平方向上的卷积，然后使用另一个1D核进行垂直方向上的卷积。这两步卷积操作串联执行，从而实现了与原始大尺寸2D核相似的效果。

  3. 计算效率提升：由于分解后的1D卷积核大大减少了参数的数量，LSKAttention在执行时的计算效率得到显著提升。这种方法特别适用于处理大尺寸的卷积核，能够有效降低内存占用和计算成本。

  4. 保持效果：虽然采用了分解和串联的策略，LSKAttention仍然能够保持类似于原始LKA的性能。这意味着在处理图像的关键特征（如边缘、纹理和形状）时，LSKAttention能够有效地捕捉到重要信息。

  5. 适用于多种任务：LSKAttention不仅在图像分类任务中表现出色，还能够在目标检测、语义分割等多种计算机视觉任务中有效应用，显示出其广泛的适用性。

总结：LSKAttention通过创新的核分解和串联卷积策略，在降低计算和内存成本的同时，保持了高效的图像处理能力，这在处理大尺寸核和复杂图像数据时特别有价值。

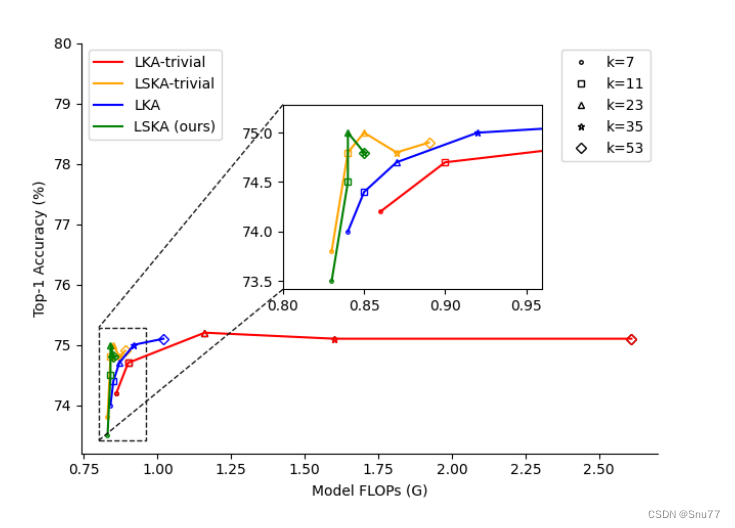
上图展示了在不同大核分解方法和核大小下的速度-精度权衡。在这个比较中，使用了不同的标记来代表不同的核大小，并且以VAN-Tiny作为对比的模型。从图中可以看出，LKA的朴素设计（LKA-trivial）以及在VAN中的实际设计，在核大小增加时会导致更高的GFLOPs（十亿浮点运算次数）。相比之下，论文提出的LSKA（Large Separable Kernel Attention）-trivial和VAN中的LSKA在核大小增加时显著降低了GFLOPs，同时没有降低性能 

上图展示了大核注意力模块不同设计的比较，具体包括：

  1. LKA-trivial：朴素的2D大核深度卷积（DW-Conv）与1×1卷积结合（图a）。
  2. LSKA-trivial：串联的水平和垂直1D大核深度卷积与1×1卷积结合（图b）。
  3. 原始LKA设计：在VAN中包括标准深度卷积（DW-Conv）、扩张深度卷积（DW-D-Conv）和1×1卷积（图c）。
  4. 提出的LSKA设计：将LKA的前两层分解为四层，每层由两个1D卷积层组成（图d）。其中，N代表Hadamard乘积，k代表最大感受野，d代表扩张率​​。

个人总结：提出了一种创新的大型可分离核注意力（LSKA）模块，用于改进卷积神经网络（CNN）。这种模块通过将2D卷积核分解为串联的1D核，有效降低了计算复杂度和内存需求。LSKA模块在保持与标准大核注意力（LKA）模块相当的性能的同时，显示出更高的计算效率和更小的内存占用。

三、LSKAttention的代码

将下面的代码在"ultralytics/nn/modules" 目录下创建一个py文件复制粘贴进去然后按照章节四进行添加即可(需要按照有参数的注意力机制添加)。

import torch
import torch.nn as nnclass LSKA(nn.Module):def __init__(self, dim, k_size):super().__init__()self.k_size = k_sizeif k_size == 7:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,(3-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=((3-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,2), groups=dim, dilation=2)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=(2,0), groups=dim, dilation=2)elif k_size == 11:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,(3-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=((3-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,4), groups=dim, dilation=2)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=(4,0), groups=dim, dilation=2)elif k_size == 23:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 7), stride=(1,1), padding=(0,9), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(7, 1), stride=(1,1), padding=(9,0), groups=dim, dilation=3)elif k_size == 35:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 11), stride=(1,1), padding=(0,15), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(11, 1), stride=(1,1), padding=(15,0), groups=dim, dilation=3)elif k_size == 41:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 13), stride=(1,1), padding=(0,18), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(13, 1), stride=(1,1), padding=(18,0), groups=dim, dilation=3)elif k_size == 53:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 17), stride=(1,1), padding=(0,24), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(17, 1), stride=(1,1), padding=(24,0), groups=dim, dilation=3)self.conv1 = nn.Conv2d(dim, dim, 1)def forward(self, x):u = x.clone()attn = self.conv0h(x)attn = self.conv0v(attn)attn = self.conv_spatial_h(attn)attn = self.conv_spatial_v(attn)attn = self.conv1(attn)return u * attn

四、手把手教你将LSKAttention添加到你的网络结构中

4.1 LSKAttention的添加教程

添加教程这里不再重复介绍、因为专栏内容有许多，添加过程又需要截特别图片会导致文章大家读者也不通顺如果你已经会添加注意力机制了，可以跳过本章节，如果你还不会，大家可以看我下面的文章，里面详细的介绍了拿到一个任意机制(C2f、Conv、Bottleneck、Loss、DetectHead)如何添加到你的网络结构中去。

添加教程->YOLOv8改进 | 如何在网络结构中添加注意力机制、C2f、卷积、Neck、检测头

需要注意的是本文的task.py配置的代码如下(你现在不知道其是干什么用的可以看添加教程)-> 

        elif m in {LSKA}:args = [ch[f], *args]

4.2 LSKAttention的yaml文件和训练截图

4.2.1 LSKAttention的yaml文件

参数位置可以填写的有7、11、23、35、41、53(代表卷积核的大小)，具体哪个效果好可能要大家自己进行一定的尝试才可以，需要注意的是这里卷积核越大计算量就会变得越大。

​

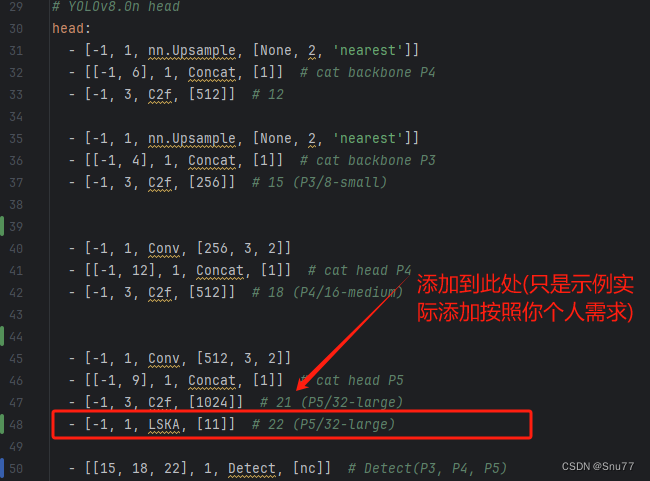
4.2.2 LSKAttention的训练过程截图 

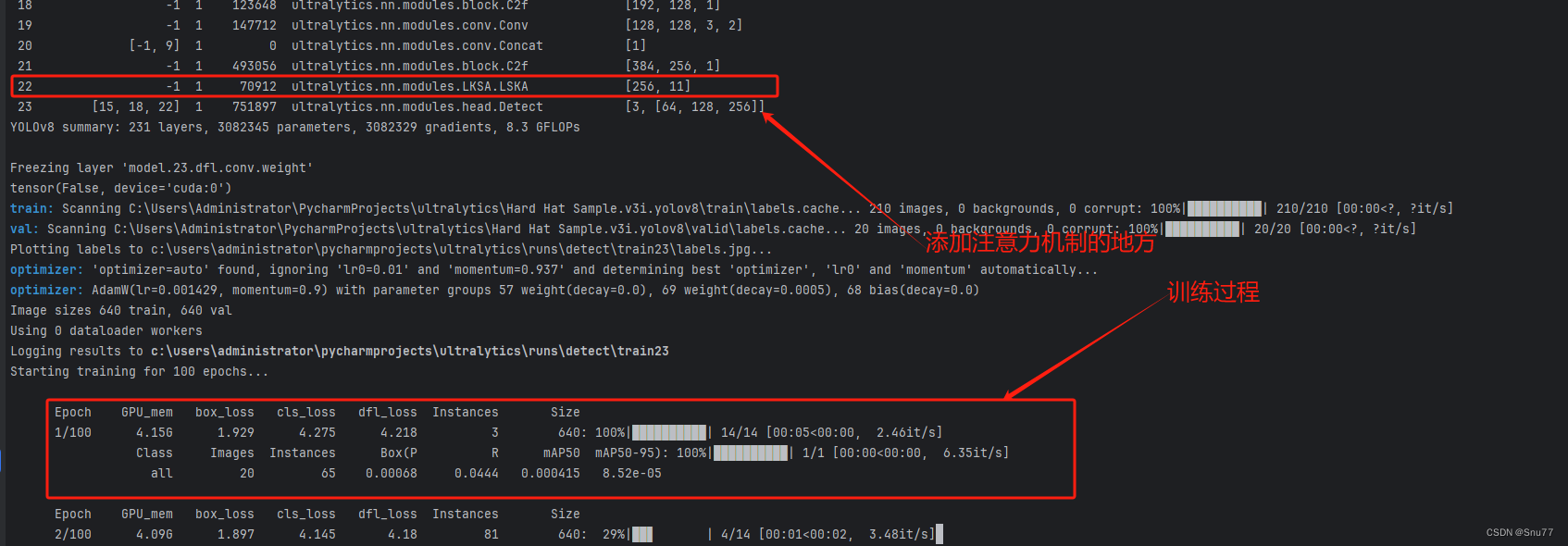
下面是我添加了LSKAttention的训练截图。

​

五、LSKAttention可添加的位置

5.1 推荐LSKAttention可添加的位置 

LSKAttention可以是一种即插即用的注意力机制，其可以添加的位置有很多，添加的位置不同效果也不同，所以我下面推荐几个添加的位，置大家可以进行参考，当然不一定要按照我推荐的地方添加。

  1. 残差连接中：在残差网络的残差连接中加入注意力机制(这个位置我推荐的原因是因为DCN放在残差里面效果挺好的大家可以尝试)

  2. 特征金字塔（SPPF）：在特征金字塔网络之前，可以帮助模型更好地融合不同尺度的特征。

  3. Neck部分：YOLOv8的Neck部分负责特征融合，这里添加注意力机制可以帮助模型更有效地融合不同层次的特征。

  4. 输出层前：在最终的输出层前加入注意力机制可以使模型在做出最终预测之前，更加集中注意力于最关键的特征。

大家可能看我描述不太懂，大家可以看下面的网络结构图中我进行了标注。

5.2图示LSKAttention可添加的位置 

​

六、本文总结 

到此本文的正式分享内容就结束了，在这里给大家推荐我的YOLOv8改进有效涨点专栏，本专栏目前为新开的平均质量分98分，后期我会根据各种最新的前沿顶会进行论文复现，也会对一些老的改进机制进行补充，目前本专栏免费阅读(暂时，大家尽早关注不迷路~)，如果大家觉得本文帮助到你了，订阅本专栏，关注后续更多的更新~

 专栏回顾：YOLOv8改进系列专栏——本专栏持续复习各种顶会内容——科研必备

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/167939.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

定制手机套餐---python序列

定制手机套餐---python序列

if __name__ __main__:print("定制手机套餐")print("")#定义电话时长：字典callTimeOptions{1:0分钟,2:50分钟,3:100分钟,4:300分钟,5:不限量}keyinput("请输入电话时长的选择编号：")valuecallTimeOptions.get(key)if val…
阅读更多...
代码随想录算法训练营第五十四天|392.判断子序列 115.不同的子序列

代码随想录算法训练营第五十四天|392.判断子序列 115.不同的子序列

文档讲解：代码随想录 视频讲解：代码随想录B站账号 状态：看了视频题解和文章解析后做出来了 392.判断子序列 class Solution:def isSubsequence(self, s: str, t: str) -> bool:dp [[0] * (len(t)1) for _ in range(len(s)1)]for i in ra…
阅读更多...
RabbitMq使用与整合

RabbitMq使用与整合

MQ基本概念 MQ概述 MQ全称 Message Queue（[kjuː]）（消息队列），是在消息的传输过程中保存消息的容器。多用于分布式系统之间进行通信。 （队列是一种容器，用于存放数据的都是容器，存…
阅读更多...
优秀的时间追踪软件Timemator for Mac轻松管理时间！

优秀的时间追踪软件Timemator for Mac轻松管理时间！

在现代社会，时间管理成为了我们工作和生活中的一大挑战。如果你经常感到时间不够用，无法高效地完成任务，那么Timemator for Mac将成为你的得力助手。 Timemator for Mac是一款出色的时间追踪软件，它可以帮助你精确记录和管理你的…
阅读更多...
Linux的基本指令 ( 一 )

Linux的基本指令 ( 一 )

目录 前言 Linux基本指令 快速认识五个指令 ls指令 补充内容 pwd指令 补充内容 cd指令 补充内容 重新认识指令 指令的本质 which指令 alias指令 最后 一个文件的三种时间 tree指令及安装 tree指令 前言 关于Linux操作系统的桌面，在学校教学中我们…
阅读更多...
实用高效 无人机光伏巡检系统助力电站可持续发展

实用高效 无人机光伏巡检系统助力电站可持续发展

近年来，我国光伏发电行业规模日益壮大，全球领先地位愈发巩固。为解决光伏电站运维中的难题，浙江某光伏电站与复亚智能达成战略合作，共同推出全自动无人机光伏巡检系统，旨在提高发电效率、降低运维成本，最大…
阅读更多...
Spark---SparkCore（一）

Spark---SparkCore（一）

一、术语与宽窄依赖 1、术语解释 1、Master(standalone):资源管理的主节点（进程） 2、Cluster Manager:在集群上获取资源的外部服务(例如：standalone,Mesos,Yarn) 3、Worker Node(standalone):资源管理的从节点(进程)或者说管理本机资源的…
阅读更多...
用Python写一个浏览器集群框架

用Python写一个浏览器集群框架

更多Python学习内容：ipengtao.com 在分布式爬虫和大规模数据采集的场景中，使用浏览器集群是一种有效的方式，可以提高数据采集的速度和效率。本文将介绍如何用Python编写一个简单但强大的浏览器集群框架，以应对需要使用多个浏览器实…
阅读更多...
WebGL/threeJS面试题扫描与总结

WebGL/threeJS面试题扫描与总结

什么是 WebGL？什么是 Three.js？请解释three.js中的WebGL和Canvas的区别？ WebGL(全写Web Graphics Library)是一种3D绘图协议，这种绘图技术标准允许把JavaScript和OpenGL ES 2.0结合在一起，通过增加OpenGL ES 2.0的一个…
阅读更多...
思科模拟器操作命令

思科模拟器操作命令

模式 思科模拟器常见的模式有 用户模式 能够操作的命令比较少 特权模式特权模式下面可以操作的比较多 全局模式 接口模式 用户模式进入特权模式: 命令enable 特权模式进行全局模式命令: configure terminal 退出命令 exit命令：返回上一层，即一步一步…
阅读更多...
RocketMQ 消息中间件 知识点汇总

RocketMQ 消息中间件 知识点汇总

目录 RocketMQ1、什么是RocketMQ？常用术语：2、为什么需要消息队列3、什么是异步处理4、什么是服务解耦5、什么是流量控制6、消息队列两种模型队列模型：发布/订阅模型：总结：7、怎么保证消息不丢失8、如何处理消息被重复消费**出现消息重复的情况：****解决方法：**9、如何保…
阅读更多...
流量分析-PhishingEmail_WriteUp

流量分析-PhishingEmail_WriteUp

一、题目问题 问题1：黑客的email名称 问题2：黑客向几人发送了钓鱼邮件 问题3：黑客传输的木马文件名 问题4：下载并运行了木马文件的人的email名称和ip地址，用“-”连接 问题5：黑客用于反弹shell的主机i…
阅读更多...
什么葡萄酒会适用这种双重滗析方法呢？

什么葡萄酒会适用这种双重滗析方法呢？

滗析有两个主要目的，一种是去除陈年或未经过滤的葡萄酒中的沉淀物。虽然沉淀物不会对你造成任何伤害，但当喝葡萄酒满嘴都是葡萄沉淀物时是一件很糟糕的事。其次，倾析葡萄酒是可以让葡萄酒“呼吸”与氧气接触的，氧气可以软化单宁&a…
阅读更多...
LeetCode Hot100 102.二叉树的层序遍历

LeetCode Hot100 102.二叉树的层序遍历

题目&#xff1a; 给你二叉树的根节点 root &#xff0c;返回其节点值的 层序遍历 。 &#xff08;即逐层地&#xff0c;从左到右访问所有节点&#xff09;。 方法&#xff1a;迭代 class Solution {public List<List<Integer>> levelOrder(TreeNode root) {if …
阅读更多...
C语言——输入一个4位正整数，输出其逆数。

C语言——输入一个4位正整数，输出其逆数。

#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int main() {int i,j 0;int a1,a2,a3,a4;printf("输入一个4位正整数&#xff1a;\n");scanf("%d",&i);a1 i/1000; a2 i/100%10; a3 i/10%10; a4 i%10; printf("千位a1%d,百位a…
阅读更多...
80C51单片机----数据传送类指令

80C51单片机----数据传送类指令

目录 一.一般传送指令&#xff0c;即mov指令 1.16位传送&#xff08;仅1条&#xff09; 2.8位传送 &#xff08;1&#xff09;目的字节为A&#xff08;累加器&#xff09; &#xff08;2&#xff09;目的字节为Rn(工作寄存器) &#xff08;3&#xff09;目的字节为direct…
阅读更多...
超分辨率重建

超分辨率重建

意义 客观世界的场景含有丰富多彩的信息&#xff0c;但是由于受到硬件设备的成像条件和成像方式的限制&#xff0c;难以获得原始场景中的所有信息。而且&#xff0c;硬件设备分辨率的限制会不可避免地使图像丢失某些高频细节信息。在当今信息迅猛发展的时代&#xff0c;在卫星…
阅读更多...
导入PIL时报错

导入PIL时报错

在导入PIL时，报以下错误： 查找原因 参考博客 Could not find a version that satisfies the requirement PIL (from versions: ) No matching distributi-CSDN博客，按照wheel后，安装PIL时，报如下的错误。 查找说是python版本与wheel文件版本不同，确认本机python版本 …
阅读更多...
Nginx模块开发之http handler实现流量统计（2）

Nginx模块开发之http handler实现流量统计（2）

文章目录 一、概述二、Nginx handler模块开发2.1、代码实现2.2、编写config文件2.3、编译模块到Nginx源码中2.4、修改conf文件2.5、执行效果 总结 一、概述 上一篇【Nginx模块开发之http handler实现流量统计&#xff08;1&#xff09;】使用数组在单进程实现了IP的流量统计&a…
阅读更多...
堆的实现（堆的插入、堆的删除等）超级全

堆的实现（堆的插入、堆的删除等）超级全

堆的实现&#xff08;堆的插入、堆的删除等&#xff09;超级全 文章目录 堆的实现&#xff08;堆的插入、堆的删除等&#xff09;超级全一、前期基础知识1.树结构①树的定义②树的相关概念③二叉树④满二叉树和完全二叉树a.满二叉树b.完全二叉树 ⑤二叉树的性质⑥二叉树顺序结构…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023