前言

也是说到做到，来做搜索的题（虽然有点拖，但是无伤大雅）。
八皇后，经典的搜索和回溯题，只要学数据结构或者算法基本都会拿出来讲上一嘴或者做一做。想当年说数据结构时对深搜还不太明白，但是学算法时竟然没有看任何提示和题解就自己把n皇后做出来了，当时就很高兴，感觉自己进步了很多。
现在我们就来重温一下这道经典的题目吧！

题目

题目描述

一个如下的 $6\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

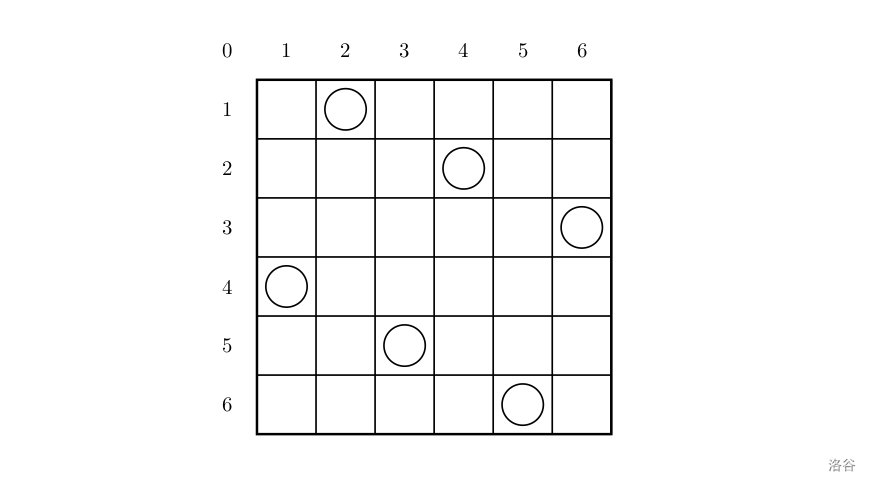
上面的布局可以用序列 $246135$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $123456$

列号 $246135$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

6

样例输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

提示

【数据范围】
对于 $100\%$ 的数据，$6\le n\le 13$。

题目翻译来自NOCOW。

题目分析

  很容易想到使用深搜+回溯，或者换简单来说，使用递归的方法，每层递归就对应一行，一行一行下来，到达最后一行都可行就在统计上加一。然后我们就需要确定哪个点是可行点。
  难点就在对对角线的判断。新的皇后是点(index,i)，我们要判断他和上面任意一个皇后(j,queen[j])不在同一条对角线上，那么就是既不在y=x+a上，也不在y=-x+a上，我们可以发现第一条线y-x和第二条线y+x都恒等于a，所以只要不相等那么就是不在同一条对角线上。所以就有了`queen[j]+j!=i+index&&queen[j]-j!=i-index``
  但是这样复杂度还是有点高呢，因为想要判断与上述所有行能否符合条件，所以过不了最后一个点。需要想出一个方法既然判断符合又只需要判断一次。
  所以我们需要转变思路，本来是每一行的每一个点都需要都要与前面的比较，现在我们想能不能在每个点确定以后就更新一份数组（白名单），使得可以让下次选点在白名单内的就是可行的，于是我们需要确定三个数组，一个是竖列，其他两个是他的向左下和右下的对角线。
然后就拿下了

注意事项

1.只输出前三个解
2.数组开大一些，不要像我只开了13，-_-
3.记得恢复现场（深搜必备注意事项）

代码

深搜+回溯

#include<iostream>
#include<algorithm>
#define MaxN  13//n皇后的最大值 
using namespace std;
int queen[MaxN+1]={0},n,total=0;
int a[25]={0},b[25]={0},c[25]={0};
void printqueen(int queen[MaxN+1]) //打印
{for(int i = 1 ; i <= n; i++) {cout<<queen[i]<<" ";}cout<<endl;}
void dfs(int index) //没有return因为并不是每个dfs都会进入下一层
{if(index==n+1) { //说明已经完成n行，可以计数了total++;if(total<=3)//前三个才打印printqueen(queen);return;}for(int i = 1; i <= n ; i++) {if(!a[i]&&!b[index+i]&&!c[index-i+n]) {queen[index]=i;//存储a[i]=1;b[index+i]=1;c[index-i+n]=1; dfs(index+1);//进入下一层a[i]=0;//恢复 b[index+i]=0;c[index-i+n]=0;}}}int main()
{cin>>n;dfs(1);//从第一层开始cout<<total;return 0;
}

打表

想不到还有打表吧，哈哈哈。确实有时候很难想到

#include<iostream>
using namespace std;
int main()
{int n;cin>>n;if(n==6) //打表进行中......{puts("2 4 6 1 3 5");puts("3 6 2 5 1 4");puts("4 1 5 2 6 3");puts("4");}if(n==7){puts("1 3 5 7 2 4 6");puts("1 4 7 3 6 2 5");puts("1 5 2 6 3 7 4");puts("40");}if(n==8){puts("1 5 8 6 3 7 2 4");puts("1 6 8 3 7 4 2 5");puts("1 7 4 6 8 2 5 3");puts("92");}if(n==9){puts("1 3 6 8 2 4 9 7 5");puts("1 3 7 2 8 5 9 4 6");puts("1 3 8 6 9 2 5 7 4");puts("352");}if(n==10){puts("1 3 6 8 10 5 9 2 4 7");puts("1 3 6 9 7 10 4 2 5 8");puts("1 3 6 9 7 10 4 2 8 5");puts("724");}if(n==11){puts("1 3 5 7 9 11 2 4 6 8 10");puts("1 3 6 9 2 8 11 4 7 5 10");puts("1 3 7 9 4 2 10 6 11 5 8");puts("2680");}if(n==12){puts("1 3 5 8 10 12 6 11 2 7 9 4");puts("1 3 5 10 8 11 2 12 6 9 7 4");puts("1 3 5 10 8 11 2 12 7 9 4 6");puts("14200");}if(n==13){puts("1 3 5 2 9 12 10 13 4 6 8 11 7");puts("1 3 5 7 9 11 13 2 4 6 8 10 12");puts("1 3 5 7 12 10 13 6 4 2 8 11 9");puts("73712");}return 0;
}

后话

额外测试用例

样例输入 #2

13

样例输出 #2

1 3 5 2 9 12 10 13 4 6 8 11 7
1 3 5 7 9 11 13 2 4 6 8 10 12
1 3 5 7 12 10 13 6 4 2 8 11 9
73712

王婆卖瓜

感觉有收获或者想跟上我的进度刷题的，可以点个关注，或者点赞收藏评论都可以！

题目来源

USACO Training Section 1.5
洛谷链接