计数排序算法

计数排序

计数排序说明：

计数排序（Counting Sort）是一种非比较性的排序算法，它通过统计元素出现的次数，然后根据元素出现的次数将元素排列在正确的位置上，从而实现排序。计数排序适用于非负整数或者具有确定范围的元素排序，其核心思想是利用一个辅助的计数数组来统计元素出现的次数，并根据次数将元素放置到正确的位置。

以下是计数排序的详细算法原理：

找到最大值：首先，我们需要遍历待排序的数组，找到其中的最大值，假设最大值为 k。
创建计数数组：接下来，我们创建一个长度为 k+1 的计数数组 count，并将数组中所有元素初始化为 0。计数数组的索引范围是 0 到 k，每个索引对应一个待排序元素的值。
统计元素出现次数：遍历待排序的数组，统计每个元素出现的次数，并将统计结果存储在计数数组 count 中。例如，如果数组中有两个元素的值都是 3，那么 count[3] 的值将变为 2。
计算累加次数：遍历计数数组 count，计算每个元素在排序后的数组中的累加次数。累加次数表示小于或等于当前元素值的元素个数。具体计算方法是通过累加前一个元素的次数得到当前元素的累加次数。这样，count[i] 就表示在排序后的数组中，小于或等于元素 i 的元素个数。
排序：创建一个与待排序数组相同长度的临时数组 sortedArr，用于存储排序结果。然后，遍历待排序数组，根据计数数组 count 中对应元素的累加次数，将每个元素放到正确的位置上。具体做法是找到当前元素在排序后数组中的索引位置，将其放入 sortedArr 数组的相应位置。同时，更新计数数组 count 中对应元素的累加次数，使其减少 1。这样，相同元素的相对顺序会保持不变。
完成排序：当遍历完待排序数组后，sortedArr 中就存储了排好序的结果。

计数排序是一种稳定的排序算法，因为相同元素的相对顺序不会改变。它适用于非负整数或者具有确定范围的元素排序，且时间复杂度为 O(n + k)，其中 n 是元素个数，k 是待排序元素的最大值。

图解演示：

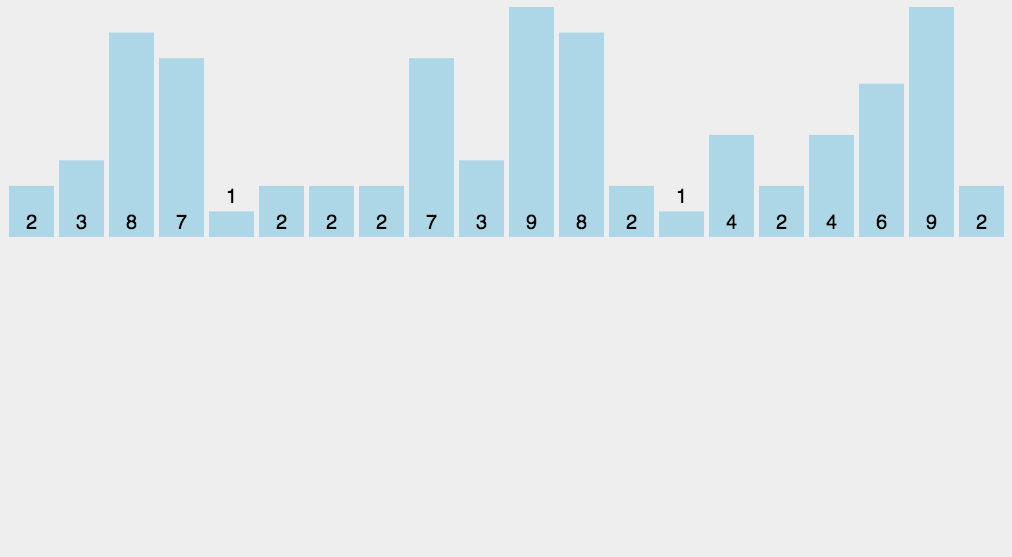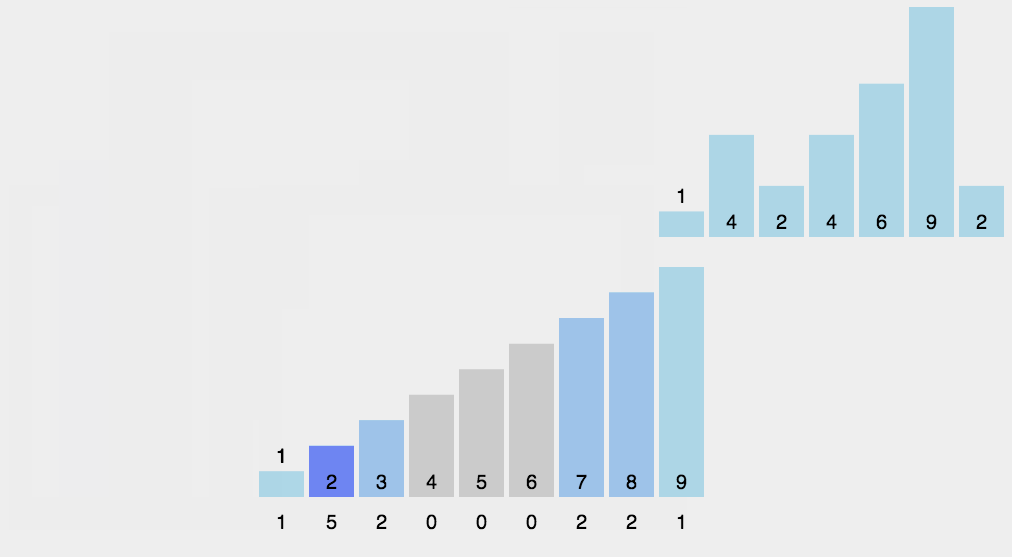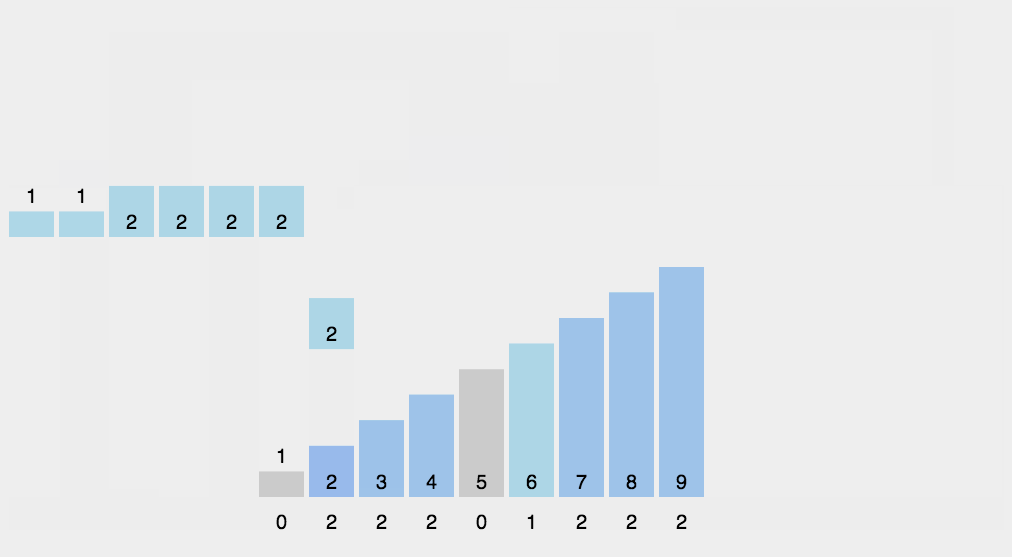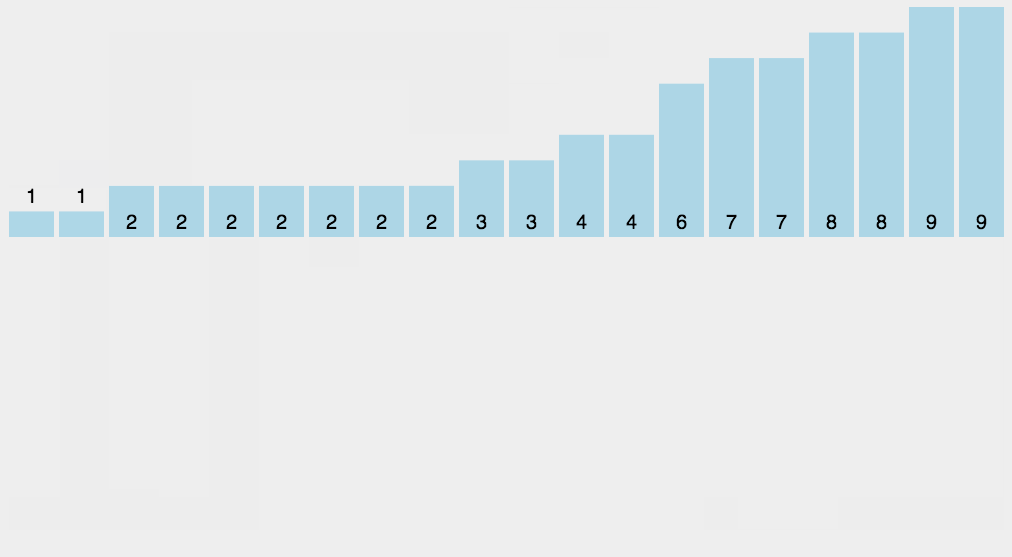
在这里插入图片描述

当使用计数排序时，需要注意以下几点情况：

计数排序适用于非负整数或者具有确定范围的元素排序。如果待排序的元素包含负数，计数排序不适用。
计数排序的时间复杂度为 O(n + k)，其中 n 是元素个数，k 是待排序元素的最大值。当元素个数 n 较大，且最大值 k 较小时，计数排序是一个高效的排序算法。但如果 k 过大，导致计数数组非常庞大，可能会造成内存的浪费。
计数排序是稳定的排序算法，相同元素的相对顺序在排序后保持不变

下面是使用 Go 语言实现计数排序的代码示例：

package mainimport "fmt"func countingSort(arr []int) []int {// 找到最大值，确定计数数组的长度max := arr[0]for _, num := range arr {if num > max {max = num}}// 创建计数数组并统计元素出现次数count := make([]int, max+1)sortedArr := make([]int, len(arr))for _, num := range arr {count[num]++}// 计算累加次数for i := 1; i <= max; i++ {count[i] += count[i-1]}// 排序并构建 sortedArrfor i := len(arr) - 1; i >= 0; i-- {sortedArr[count[arr[i]]-1] = arr[i]count[arr[i]]--}return sortedArr
}func main() {arr := []int{4, 2, 2, 8, 3, 3, 1}fmt.Println("Unsorted array:", arr)arr = countingSort(arr)fmt.Println("Sorted array:", arr)
}