红黑树:
一种接近平衡的二叉树,平衡程度低于搜索二叉树。
特点:
1.根节点为黑
2.黑色结点的子结点可以是红色结点或黑色结点。
3.红色结点的子结点只能是黑色结点。
4.每个结点到其所有叶子结点的路径的黑色结点个数相同。
5.指向空的结点,指向空的那一侧视为指向黑色结点(指向nullptr的黑色结点,用于明确路径)
6.由于上述规则,使得红黑树任意结点的左右子树高度差不超过二倍(最小是全黑,最大是红黑相交,又由于黑色结点个数需要一致,因此高度不会超过二倍)。
模拟实现红黑树:
1.红黑树的插入:
// 注意:为了简单起见,本次实现红黑树不存储重复性元素bool Insert(const T& data){if (_pHead == nullptr){Node* cur = new Node(data);_pHead = cur;_pHead->_color = black;return true;}//有根节点的时候Node* cur = new Node(data);Node* news = _pHead;Node* parent = nullptr;//查找插入位置while (news != nullptr){if (news->_data < data){ parent = news;news = news->_pRight;}else if (news->_data > data){ parent = news;news = news->_pLeft;}else{return false;}}//确定插入位置是parent的左还是右if (parent->_data < data){parent->_pRight = cur;cur->_pParent = parent;}else{parent->_pLeft = cur;cur->_pParent = parent;}//开始向上判断//若父节点为黑则可以正常插入,无任何影响//父节点为红才进入,若父节点为空则cur指向根结点同样退出while (parent&&parent->_color==red){ Node* grandparent = parent->_pParent;//parent为红则一定有父节点if(grandparent->_color==black){//得到uncleNode* uncle = nullptr;if (parent->_data < grandparent->_data){uncle = grandparent->_pRight;}else{uncle = grandparent->_pLeft;}//判断uncle情况if (uncle && uncle->_color == red){ //UNCLE存在且是红parent->_color = uncle->_color = black;grandparent->_color = red;cur = grandparent;parent = cur->_pParent;}else{//uncle为黑或者uncle为空if (cur == parent->_pLeft&& parent == grandparent->_pLeft){//右旋RotateR(grandparent);//更新颜色parent->_color = black;grandparent->_color = red;}else if (cur == parent->_pRight&& parent == grandparent->_pRight){//左旋RotateL(grandparent);//更新颜色parent->_color = black;grandparent->_color = red;}//更新后当前子树的根节点为黑,无需向上继续判断,因此parent->_color可以直接使得退出循环else if(cur == parent->_pRight&& parent == grandparent->_pLeft){//先左旋parent再右旋grandparentRotateL(parent);RotateR(grandparent);cur->_color = black;grandparent->_color = red;break;}else{RotateR(parent);RotateL(grandparent);cur->_color = black;grandparent->_color = red;break;}}}else{ //此时grandparent和parent颜色均是红,报错cout << parent->_data<<"出现连续红结点" << endl;assert(false);}}_pHead->_color = black;}// 左单旋void RotateL(Node* pParent){Node* parent = pParent;Node* pr = parent->_pRight;Node* prl = pr->_pLeft;//记录父节点Node* pp = parent->_pParent;//更新指针parent->_pRight = prl;if (prl)//判断prl是否存在prl->_pParent = parent;pr->_pLeft = parent;parent->_pParent = pr;if (pp == nullptr){//若parent是根节点_pHead = pr;pr->_pParent = nullptr;}else{ //父节点连接if (pp->_data < parent->_data){pp->_pRight = pr;pr->_pParent = pp;}else{pp->_pLeft = pr;pr->_pParent = pp;}}}// 右单旋void RotateR(Node* pParent){Node* parent = pParent;Node* pl = parent->_pLeft;Node* plr = pl->_pRight;//记录父节点Node* pp = parent->_pParent;//更新指针parent->_pLeft = plr;if (plr)//判断prl是否存在plr->_pParent = parent;pl->_pRight = parent;parent->_pParent = pl;if (pp == nullptr){//若parent是根节点_pHead = pl;pl->_pParent = nullptr;}else{ //父节点连接if (pp->_data < parent->_data){pp->_pRight = pl;pl->_pParent = pp;}else{pp->_pLeft = pl;pl->_pParent = pp;}}}插入一个结点,初始时插入结点为红(若为黑则会导致其祖先结点每条路径黑色结点的个数改变,修改十分麻烦)。若此时父节点为黑,则无需进行任何其余操作。
若父节点为红,此时会出现连续红色结点的情况,不符合红黑树的定义,因此需要修改。
修改主要分以下几种情况:
1.
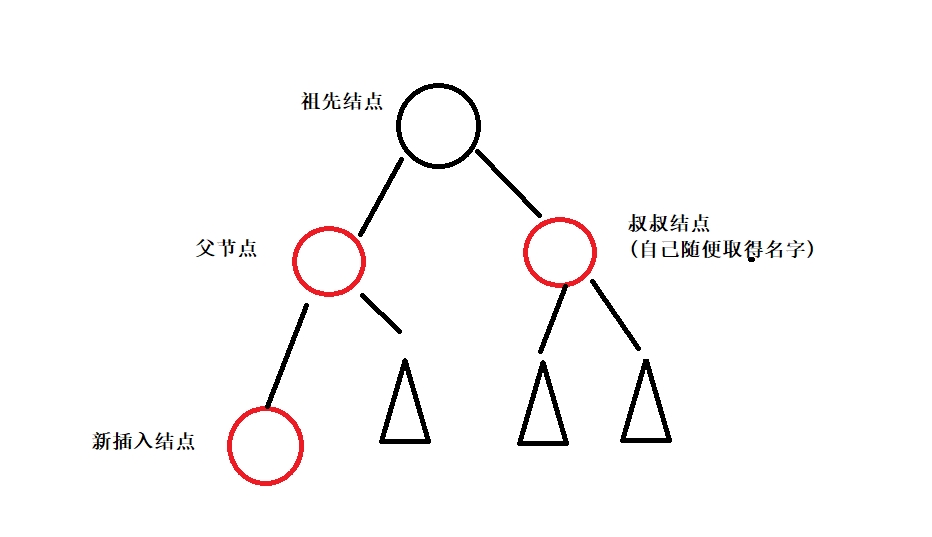
此时叔叔结点存在且为红色。
修改方式是将父节点和叔叔结点改成黑色,祖先结点改成红色,然后将祖先结点视为新插入结点继续向上判断。此时父节点和叔叔结点改成黑色,不会受其子节点颜色的影响,且对于祖先结点的父节点,每条路径的黑色结点的个数没有变化,因此仍符合红黑树。
2.
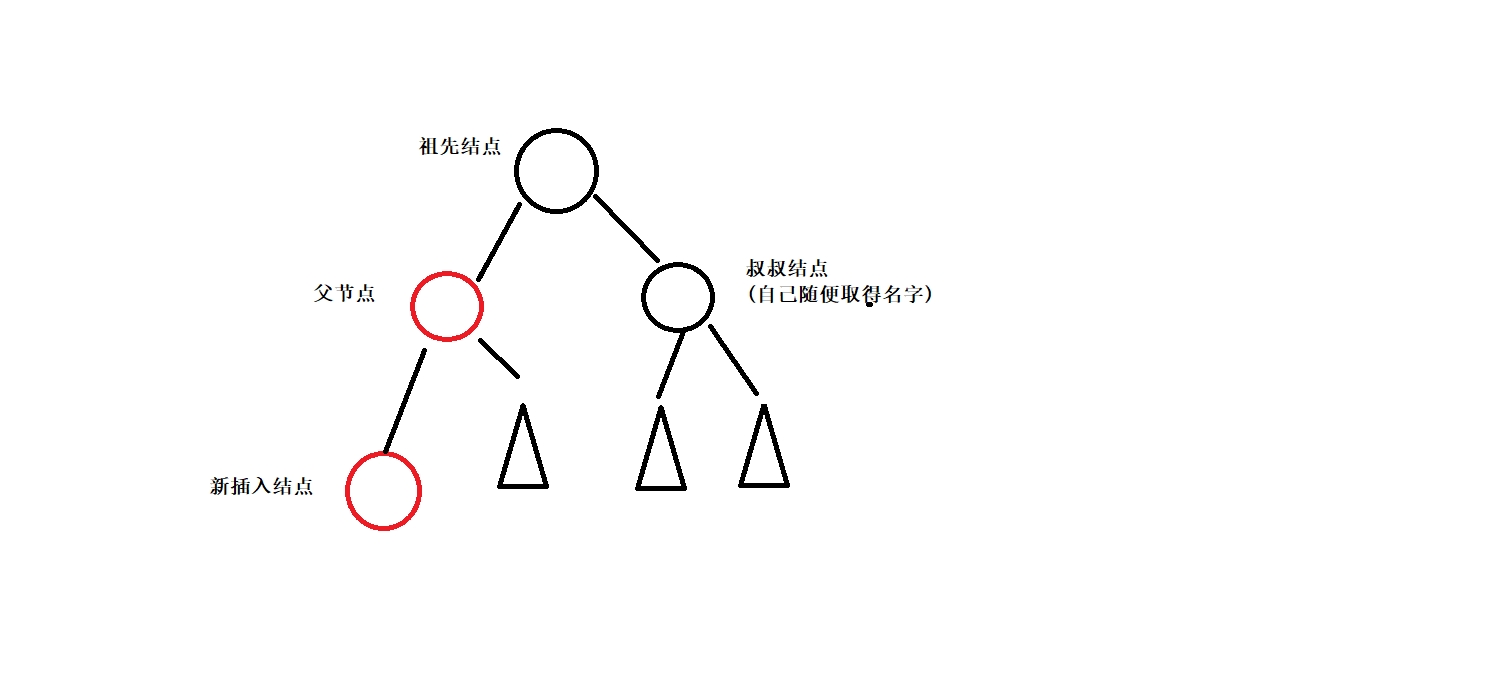
此时叔叔结点为黑色结点或者不存在(不存在的情况,根据红黑树规则指向空的结点,指向空的那一侧视为指向黑色结点,因此也可以看做叔叔结点为黑色结点)。此时需要进行旋转来修改这棵子树。若祖先结点和父节点以及新插入结点都在同一侧(比如父节点是祖先结点左子树,新插入结点是父节点的左子树),则只需要对祖先结点进行一次旋转,旋转完成后将父节点改成黑色,祖先结点改成红色即可。若不在同一侧,则需要先对父节点进行一次旋转,再对祖先结点进行一次旋转,旋转完成后新插入结点的颜色为黑,祖先结点颜色为红。
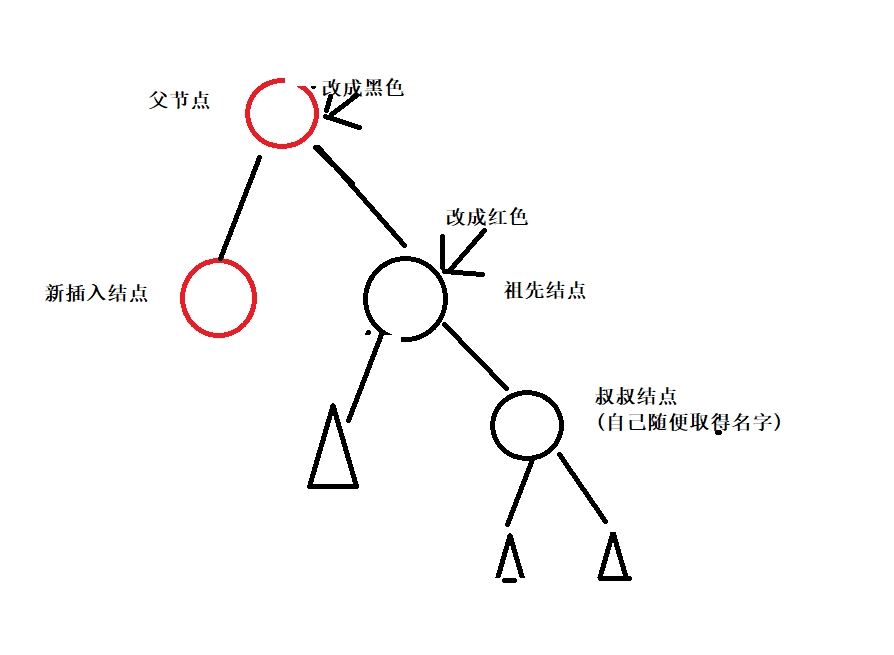
在同一侧的旋转一次。
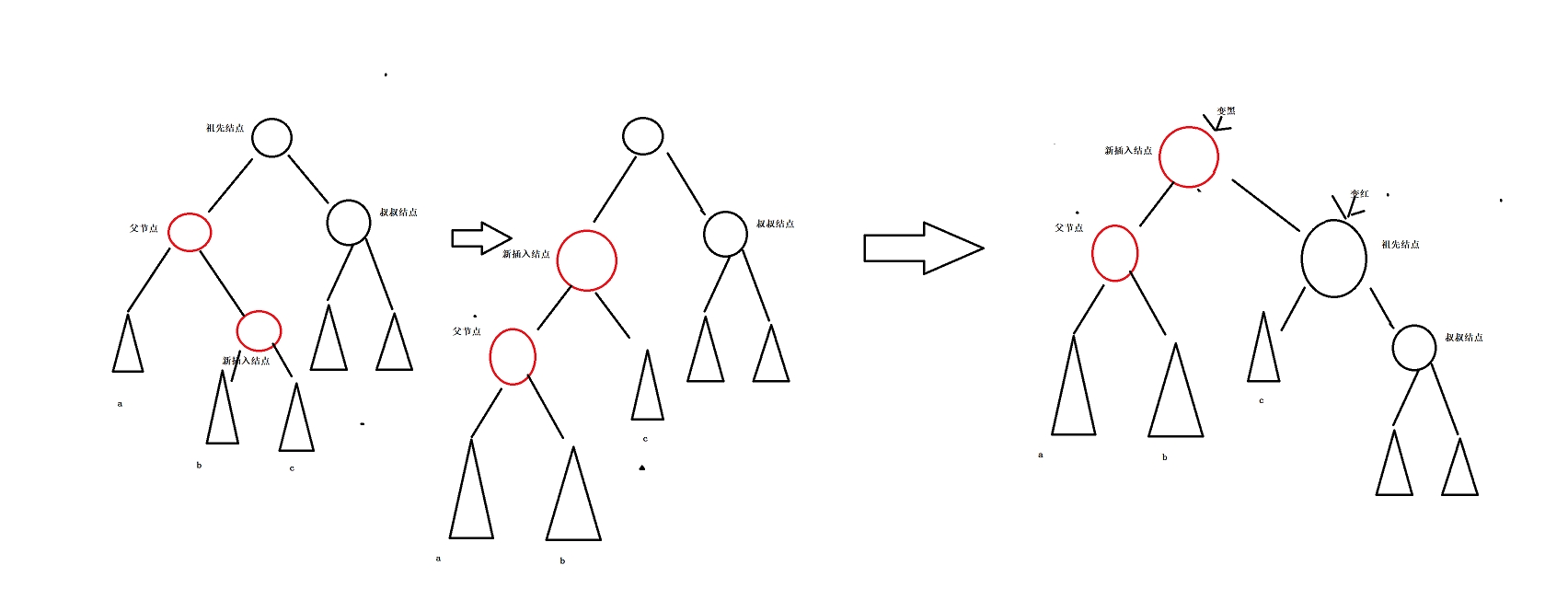
不在同一侧,旋转两次。

)

)


)
】文件和异常详解:使用、读取、写入、追加、保存用户的信息,以及优雅的处理异常)


)







)
