1. 知识简介
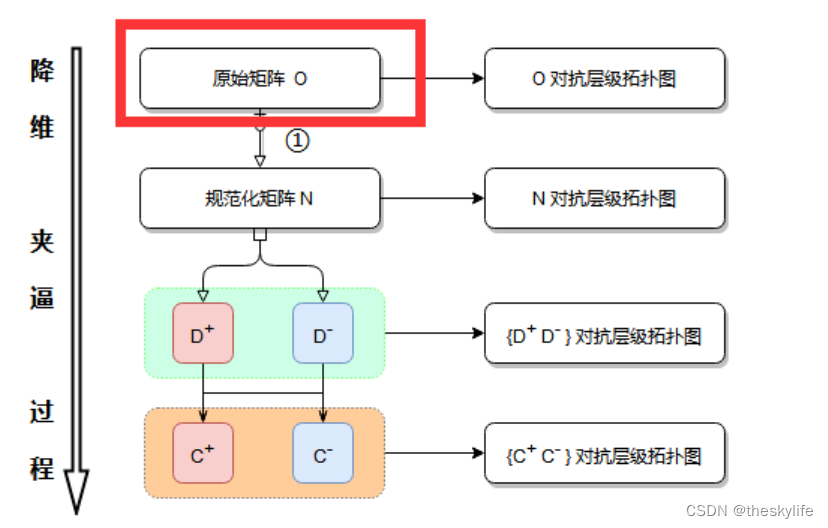
数据归一化是数据预处理的一项重要步骤,它对于提高模型性能、加速模型训练、避免数值计算问题以及提高模型的泛化能力都具有重要作用。进行数据归一化可以起到以下作用:消除量纲影响,加速模型收敛,提高模型性能,防止数值计算问题,提高模型泛化能,更好地处理异常值。

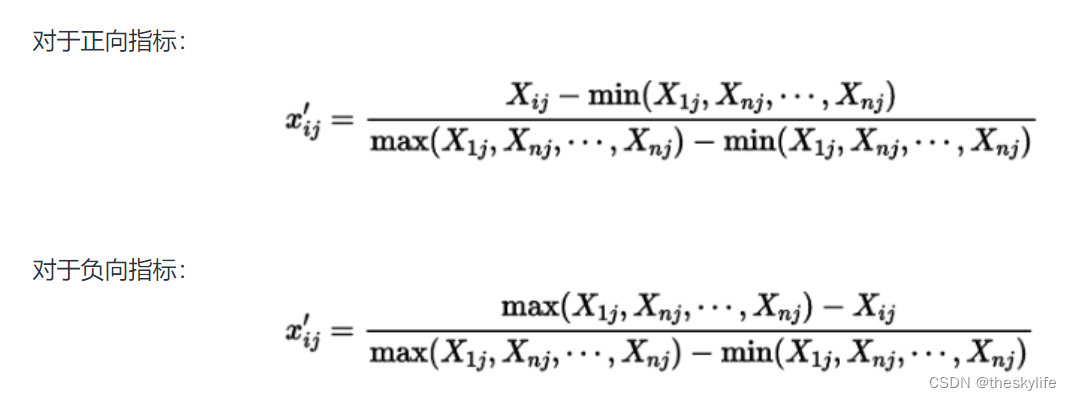
3.python中实现
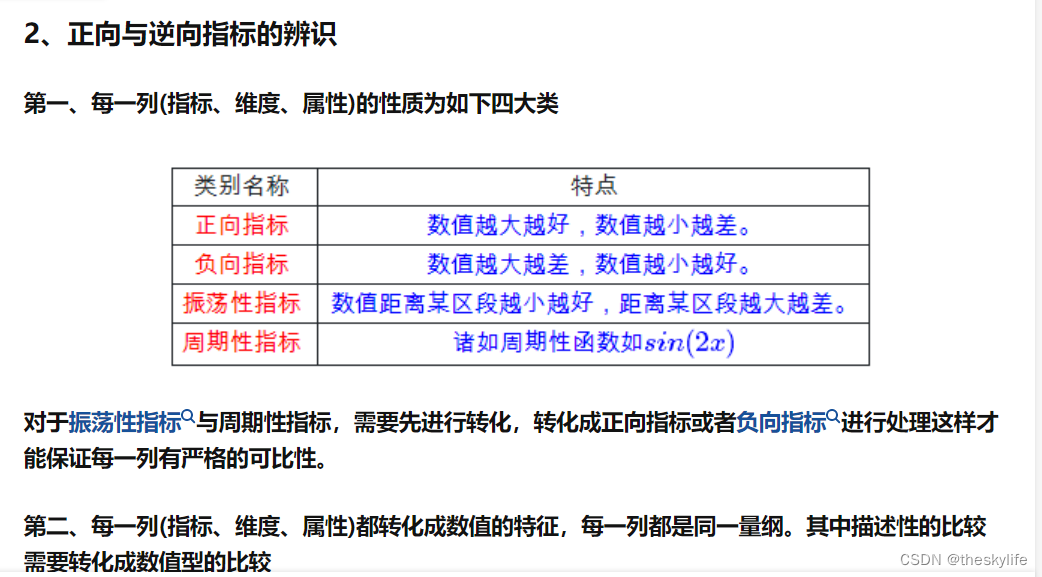
3.1 正向型指标和负向型指标
正向型指标的取值范围在0到正无穷,数值越大表示绩效越好。在归一化时,通常使用 Min-Max 归一化方法,将指标缩放到0到1之间。
负向型指标的取值范围在负无穷到0之间,数值越接近0表示绩效越好。在归一化时,也使用 Min-Max 归一化方法,将指标缩放到0到1之间,但需要注意取值范围的定义。
import numpy as np
import pandas as pddef min_max_normalize(data, method='positive', feature_range=(0, 1)):"""Min-Max归一化Parameters:- data: 需要进行处理的DataFrame- method: 归一化方向,'positive'为正向,'negative'为逆向- feature_range: 设置归一化后的最小最大值,默认为 (0, 1)Returns:- normalized_data: 归一化后的DataFrame"""y_min, y_max = feature_rangenormalized_data = pd.DataFrame()for col in data.columns:col_max, col_min = data[col].max(), data[col].min()if method == 'negative':normalized_values = (y_max - y_min) * (col_max - data[col]) / (col_max - col_min) + y_minelif method == 'positive':normalized_values = (y_max - y_min) * (data[col] - col_min) / (col_max - col_min) + y_minnormalized_data[col] = normalized_values.valuesreturn normalized_data# 示例用法
# data = pd.DataFrame({'amount': [20, 40, 30, 26], 'cost': [3, 6, 2, 10]})
# normalized_data = min_max_normalize(data[['cost']], method='negative', feature_range=(0, 1))3.2 中心倾向指标
中心倾向指标的取值范围一般视数据情况而定,数值越靠近中间位置表示绩效越好。在归一化时,通常使用 Min-Max 归一化方法,将指标缩放到0到1之间。
一些场景举例,比如财务绩效数据,利润、营业收入等中心倾向稳定的话,现实场景中,代表经营状况越好,比如生产质量控制越靠近设置的目标值越符合要求。
若是基于数据的情况,取中心位置的话,可以用以下方法:
import numpy as np
import pandas as pddef mid_normalize(data, feature_range=(0, 1)):"""中心倾向指标归一化Parameters:- data: 需要进行处理的DataFrame- feature_range: 设置归一化后的最小最大值,默认为 (0, 1)Returns:- normalized_data: 归一化后的DataFrame"""y_min, y_max = feature_rangenormalized_data = pd.DataFrame()for col in data.columns:col_max, col_min = data[col].max(), data[col].min()col_mid = (col_max + col_min) / 2normalized_values = data[col].map(lambda x: 2 * (x - col_min) / (col_max - col_min) if x < col_mid else 2 * (col_max - x) / (col_max - col_min))normalized_values *= (y_max - y_min)normalized_data[col] = normalized_values.valuesreturn normalized_data# 示例用法
#data=pd.DataFrame({'ph':[2,5,7,10,12],
# 'mid':[100,20,50,70,90],
# 'temperature':[-10,10,25,30,40]})
# normalized_data=mid_normalize(data[['ph', 'mid']])若是有给定的中心值,则可以参考一下用法:
import pandas as pddef mid_normalize(data, best_values=None, feature_range=(0, 1)):"""中心倾向指标归一化Parameters:- data: 需要进行处理的DataFrame- best_values: 中心指标值,如果为None,则使用(feature_range[0] + feature_range[1]) / 2- feature_range: 设置归一化后的最小最大值,默认为 (0, 1)Returns:- normalized_data: 归一化后的DataFrame"""y_min, y_max = feature_rangenormalized_data = pd.DataFrame()if data.empty:raise ValueError("Input DataFrame is empty.")for col_index, col in enumerate(data.columns):c_max, c_min = data[col].max(), data[col].min()if best_values is None:c_mid = (y_max + y_min) / 2else:c_mid = best_values[col_index]normalized_values = 1 - abs(data[col] - c_mid) / (c_max - c_min)normalized_values *= (y_max - y_min)normalized_data[col] = normalized_valuesreturn normalized_data# 示例用法
#data=pd.DataFrame({'ph':[2,5,7,10,12],
# 'mid':[100,20,50,70,90],
# 'temperature':[-10,10,25,30,40]})
#normalized_data = mid_normalize(data[['ph', 'mid']], [7, 50])3.3 区间型指标
区间型指标是一种度量指标,其特点是具有明确的数值区间,通常表示一个范围或区间内的值。这种类型的指标提供了更多的信息,而不仅仅是单一的数值。区间型指标在统计学、经济学、工程学、生态学等领域经常被使用。
import numpy as np
import pandas as pddef section_normalize(data, feature_range=(0, 1), target_section=(40, 60)):"""区间型指标归一化Parameters:- data: 需要进行处理的DataFrame- feature_range: 设置归一化后的最小最大值,默认为 (0, 1)- target_section: 目标区间,表示在该区间内的值将被保持不变Returns:- normalized_data: 归一化后的DataFrame"""y_min, y_max = feature_rangenormalized_data = pd.DataFrame()if data.empty:raise ValueError("Input DataFrame is empty.")for col in data.columns:col_max, col_min = data[col].max(), data[col].min()distance_to_min = max((target_section[0] - col_min), 0)distance_to_max = max((col_max - target_section[1]), 0)c = distance_to_min + distance_to_max# 区间映射函数简化normalized_values = 1 - np.abs(data[col] - np.mean(target_section)) / c# 当数值位于目标区间内时,将归一化的值设为1mask = (data[col] >= target_section[0]) & (data[col] <= target_section[1])normalized_values[mask] = 1normalized_values = np.clip(normalized_values, 0, 1)normalized_values *= (y_max - y_min)# 标记后输出normalized_data[col] = normalized_valuesreturn normalized_data# 示例用法
# normalized_data = section_normalize(data[['temperature']], target_section=(20, 30))
4.后记
数据归一化是数据分析和机器学习中必不可少的步骤之一。它可以消除量纲影响,提高模型的性能和稳定性,加快模型的收敛速度,并方便特征选择过程。通过归一化,可以更好地理解和利用数据,提高模型的准确性和可解释性。
在进行数据归一化时,需要注意选择合适的归一化范围和方法,处理异常值,确定归一化顺序,并注意归一化的逆操作。通过合理的数据归一化处理,可以更好地利用数据进行分析和建模。










——简单工厂模式)






)

