链接: 使用最小花费爬楼梯

题目描述

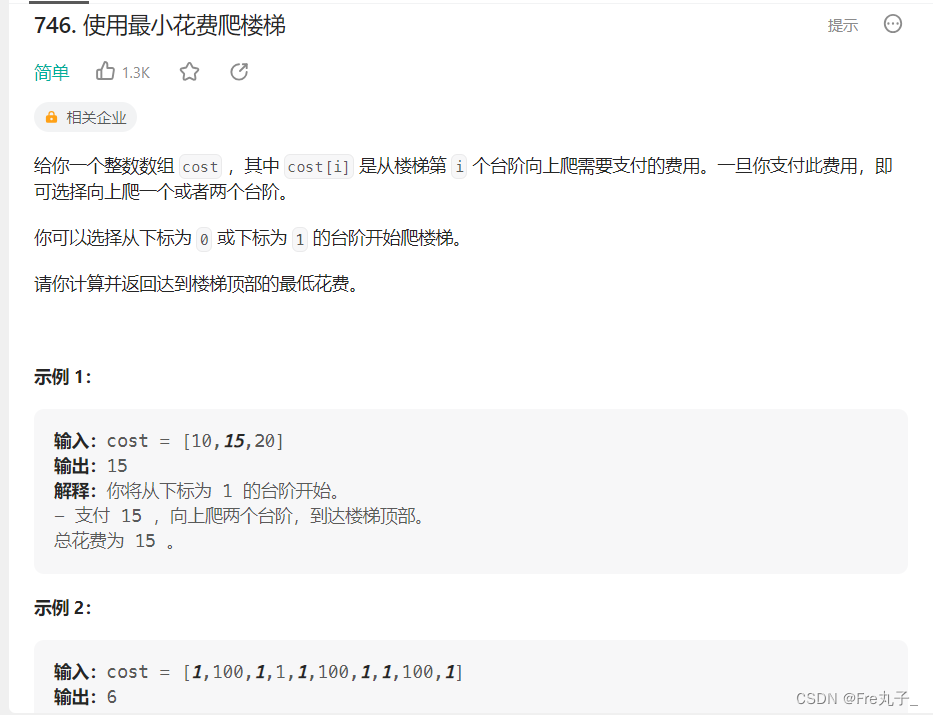
算法流程(方法一)

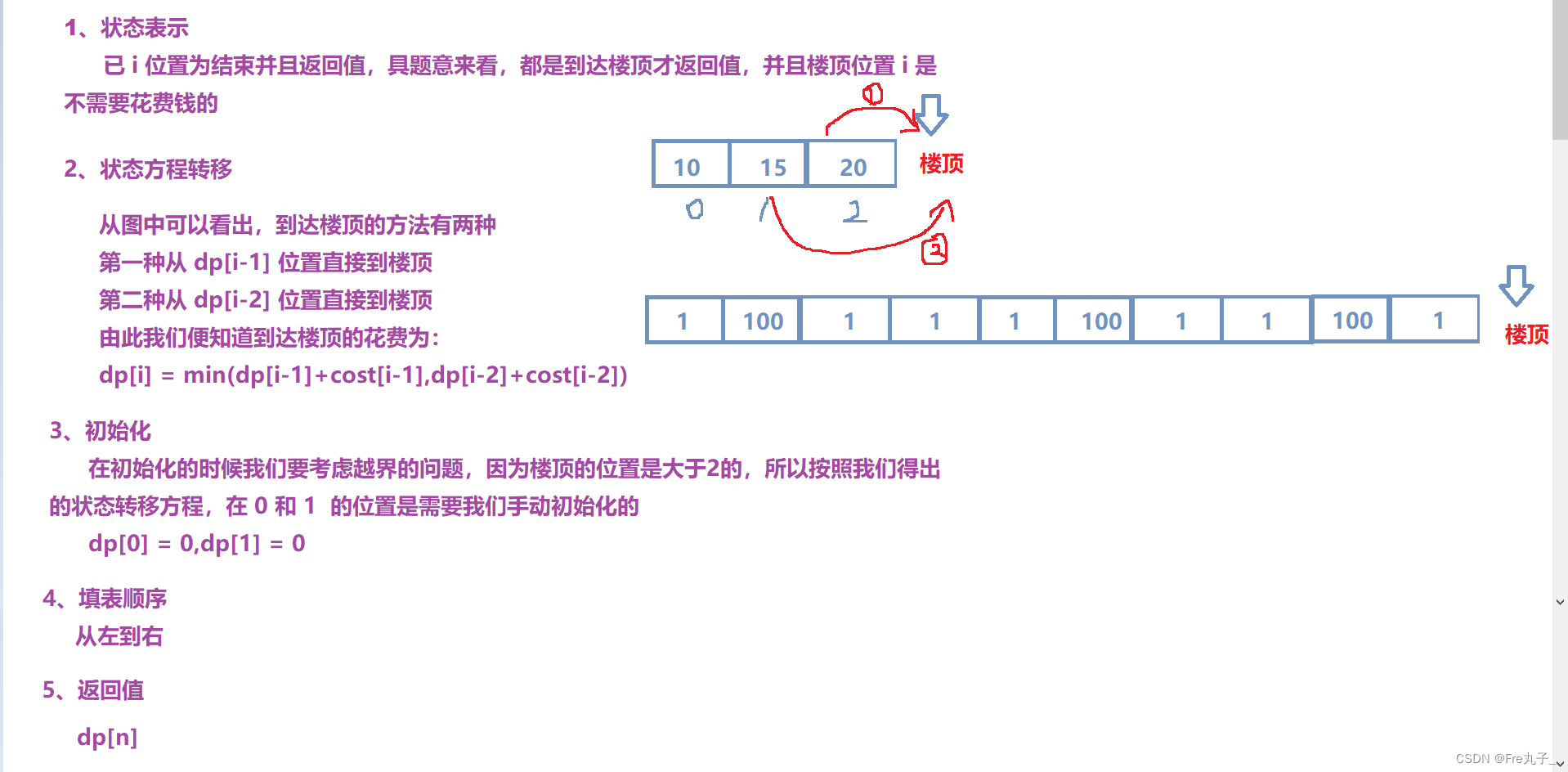
编程代码

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {size_t size = cost.size()  + 1;vector<int> dp(size);dp[0] = dp[1] = 0;for(int i = 2;i < size;++i){dp[i] = min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1]);}return dp[size-1];} 
};

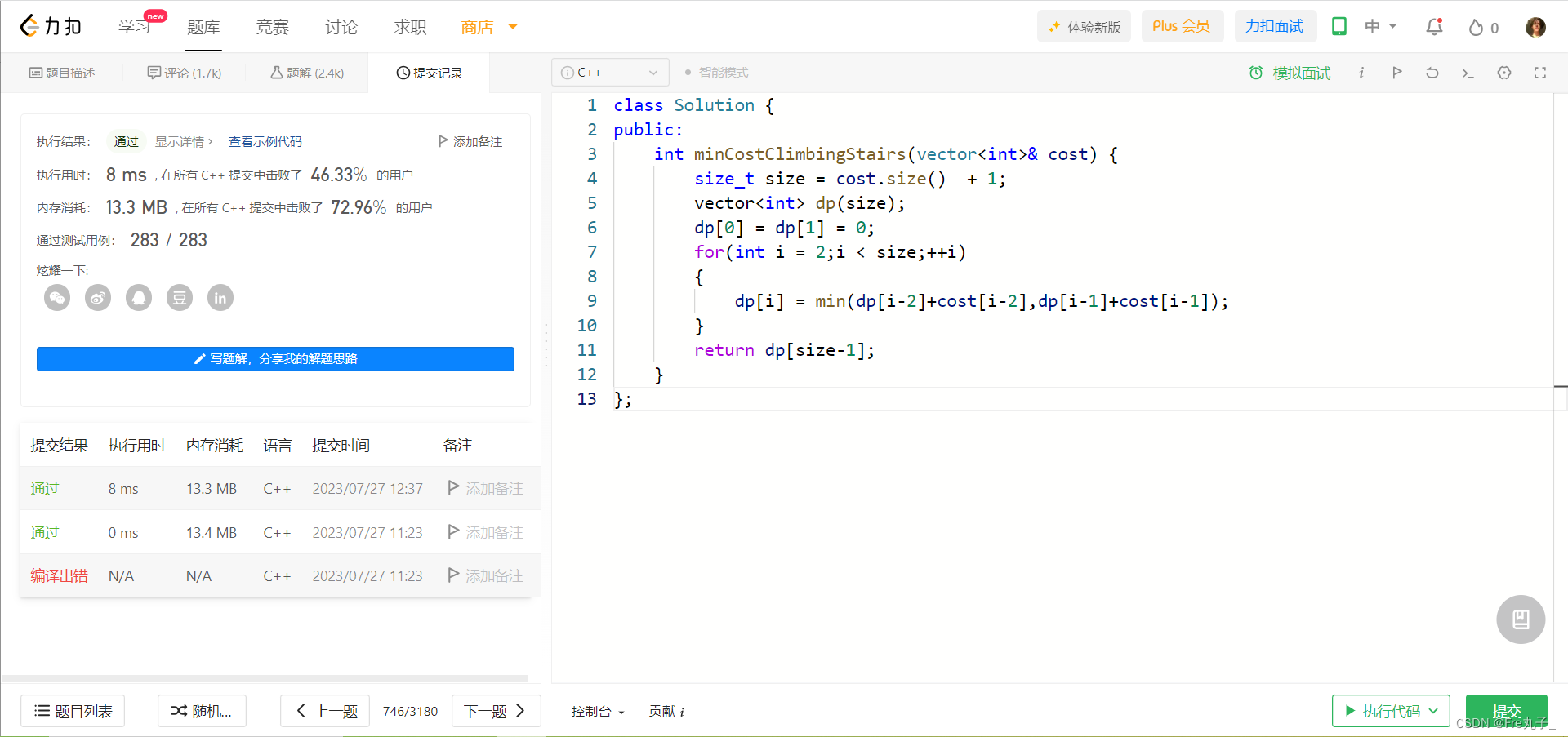
优化代码

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {size_t size = cost.size()  + 1;int a,b,c,d;a = b = 0;for(int i = 2;i < size;++i){c = min(a+cost[i-2],b+cost[i-1]);a = b;b = c;}return c;} 
};

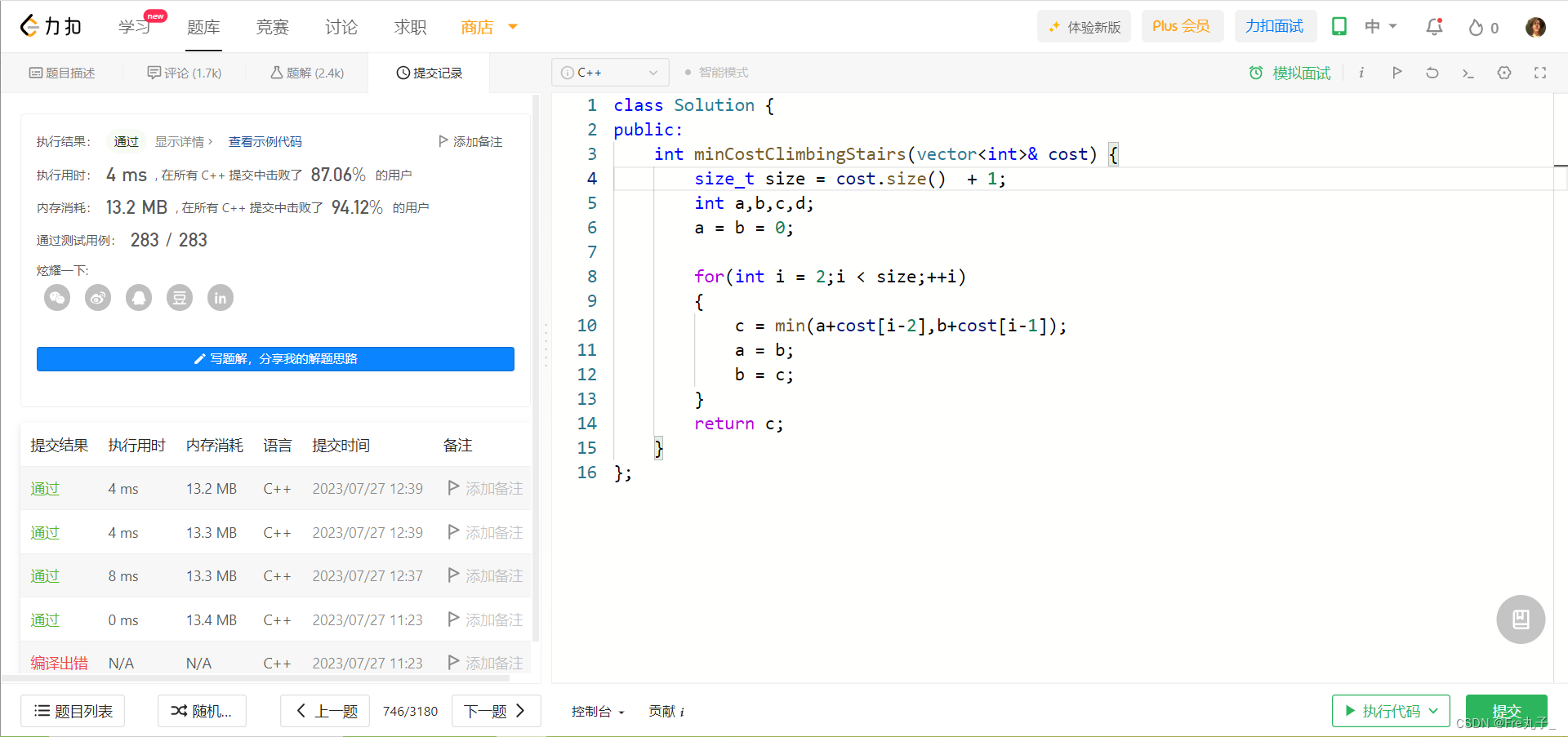
算法流程（方法二）

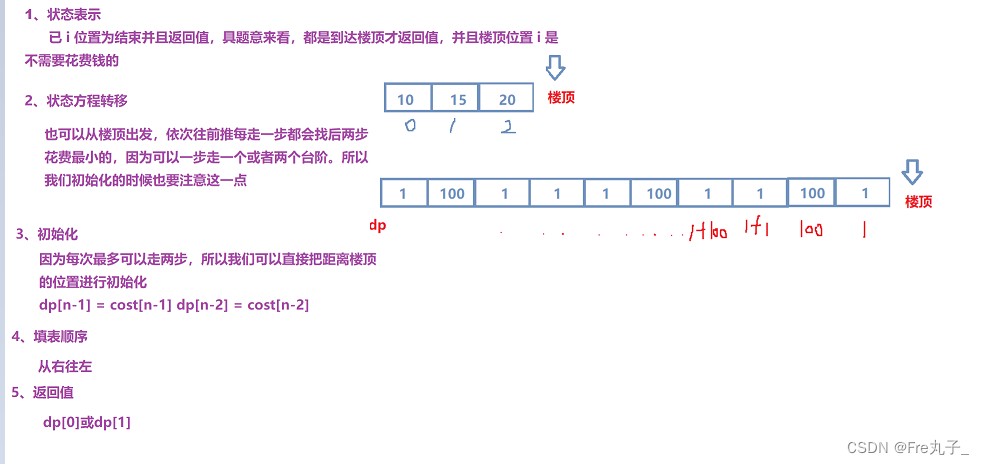
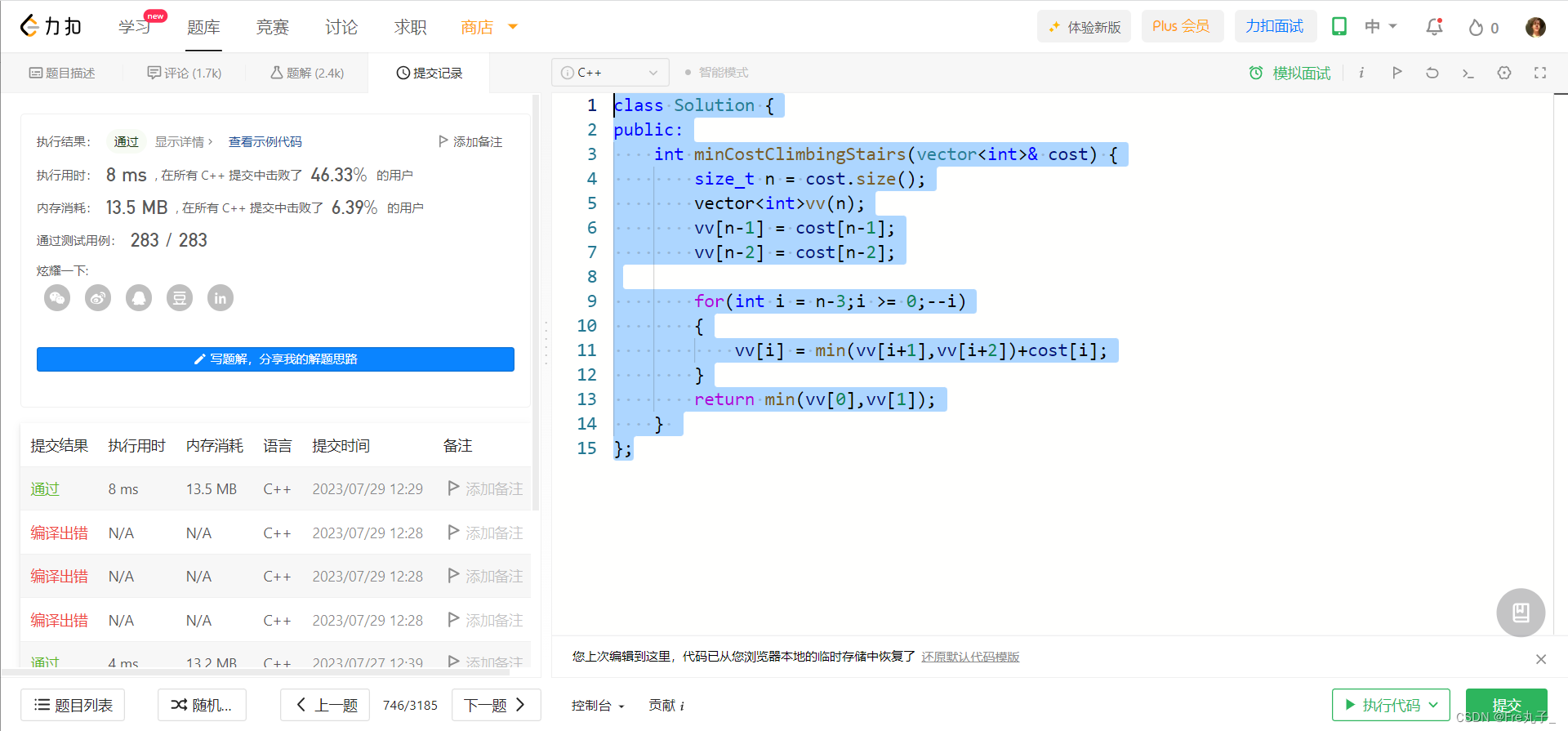
编程代码

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {size_t n = cost.size();vector<int>vv(n);vv[n-1] = cost[n-1];vv[n-2] = cost[n-2];for(int i = n-3;i >= 0;--i){vv[i] = min(vv[i+1],vv[i+2])+cost[i];}return min(vv[0],vv[1]);} 
};

代码优化

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {size_t n = cost.size();int a = cost[n-1];int b = cost[n-2];int c;for(int i = n-3;i >= 0;--i){c = min(a,b)+cost[i];a = b;b = c;}return min(a,b);} 
};