一、说明

        在在这篇文章中，我们将学习我们的第一个机器学习算法，称为简单线性回归。这是一个重要的算法，因为当您可能正在学习第一个神经网络（称为人工神经网络）时，在此算法中学习的技术也适用于深度学习。我会尝试将其分解为单独的模块，以便您可以更好地理解它（所以这是机器学习系列的第 1 部分）。线性回归，顾名思义，在监督机器学习中，回归问题陈述肯定可以借助类似的线性回归来解决。现在简单的线性回归算法到底是什么，假设我有一个数据集，并且这个特定的数据集具有体重和高度等特征。

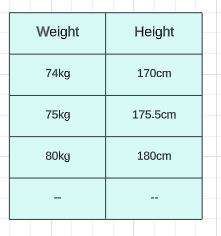
        假设体重在74 公斤左右，我的身高可能是170 厘米，如果体重在80 公斤左右，我的身高可能是180 厘米，如果体重在75 公斤左右，我的身高可能是175.5 厘米。假设在这种数据集中，我们的主要目标是每当我们给出新的权重时训练一个模型，该模型应该能够预测高度，现在你看到这个特征基本上是我们的独立特征（权重）并且这个特征特别是关于输出或依赖特征。这就是我们计划做的，我们将在简单线性回归的帮助下进行训练。那么为什么我们把它说成简单的线性回归，这样通过查看这个你就可以了解这里有多少输入特征呢？我们有一个输入特征和一个输出特征。每当我们有这一输入特征时，我们就说它是简单线性回归。如果我们有多个输入特征，那么我们可以将其称为多元线性回归。因此，在本教程中，我们尝试指定一个模型，并使用特定数据对其进行训练，稍后该模型应该能够预测高度。

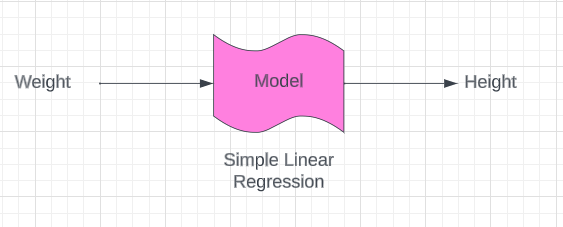
        因此，关于这个特定的数据集，让我绘制一些点。假设有一些点是这样绘制的，因此在回归的帮助下，我们要做的是创建一条最佳拟合线，而这条最佳拟合线实际上有助于预测权重。因此，让我们说一下，一旦我们获得这条最佳拟合线，预测将如何发生，并且应该以您知道真实点之间的距离的方式创建这条最佳拟合线。

        真实点是指我的数据的输出，即 170 厘米、180 厘米和 175.5 厘米。这些预测点之间的距离基本上就是误差。

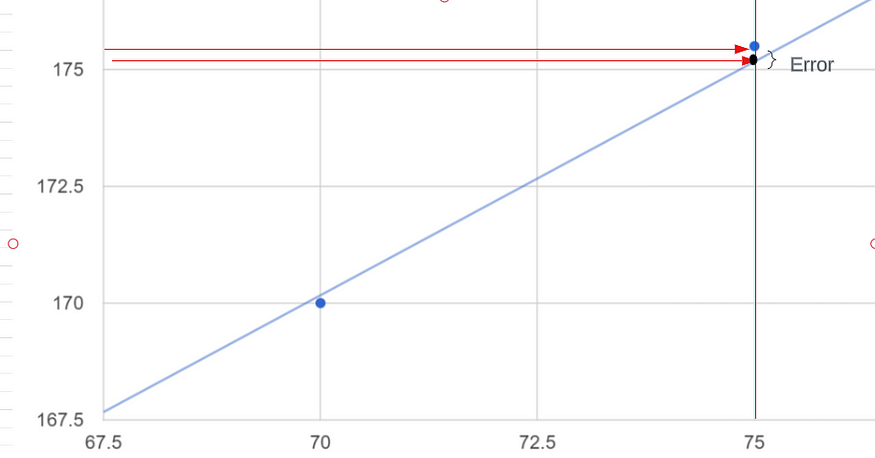
        所以这些是我的真实点（蓝色点），蓝色线是使用这些点的预测线。我们只是创建一条预测线，每当我们获得新的数据点时，它都是最佳拟合线，假设特定的重量为 72.5 公斤，我们如何预测我们的输出，这意味着高度应该是多少？我们只是从 x 轴到预测线画一条线，这是我的最佳拟合线，从最佳拟合线我将画另一条线到我的 y 轴所以这条线符合我在 y 的高度轴是我给定输入的输出。

        这就是我们在简单线性回归中所做的。让我们尝试了解该特定最佳拟合线的数学方程是什么以及最佳拟合线的具体误差是什么。在此之前，我们需要了解我在解释整个机器学习算法时实际上将使用的一些符号。所以我要画另一张图，假设这是 x 轴，我的体重在x 轴上，身高在y 轴上，我刚刚随机创建了一些点，这些点基本上提到了我们的数据集。

        我将训练我们的特定模型。我们再次计划在这里创建一条最适合的生产线。为了创建这条最佳拟合线，我们只需要一些方程，即：

y = mx + c

        如果您看过一些研究论文，他们也可能会使用类似的内容，

Y = β 0 + β 1 x

        您可能还见过这样的方程，

hθ(x)=θ0+θ1x

        我将使用特定的符号，只不过是hθ(x)=θ0+θ1x。该方程称为假设，用h(x)=θ0 +θ1x 的形式表示（基本上与 y = mx + c 相同），其中 θ0（或 c）和 θ1 是（或 m）参数。我们希望找到使我们的假设与数据最佳匹配的参数值。现在这里的 X 表示我的独立特征，即重量。请尝试理解什么是θ0和什么是θ1。首先，θ0到底是什么，我们说它是一个截距。为什么我们说它是拦截？这是通过简单的数学计算得出的。假设我的X值为零，那么会发生hθ(x)=θ0。正如您在我的图表中看到的，最佳拟合线在某处与 y 轴相交。所以我的最佳拟合线与 y 轴相交的点并将其作为拦截器。这意味着当 x 轴为零时，即θ0的值。现在我们知道θ0的含义是什么了。它只不过是一个拦截器。当我们谈论斜率或系数时，它表示 x 轴上的唯一运动以及有关 y 轴的运动。

        这由等式中的θ1表示。假设如果我有许多独立的特征，那么这个方程就变成了

        所以最后我们知道我们可以使用这个方程预测给定 x 值的y 值。我们将此预测点表示为ŷ。你知道 y 是我们的实际输出值。现在我们可以使用这两个值得到误差方程。

Error = y - ŷ

        现在我们将提出一条最佳拟合线，其中当我尝试计算或求所有这些误差的总和时，它应该是最小的。假设存在多条具有不同误差总和值的最佳拟合线。您必须选择误差总和值最小的最佳拟合线。

二、回归成本函数

        在这里，我们将找到选择最佳拟合线的优化方法。为此，我们将使用成本函数。该成本函数以符号形式给出。

        我们必须创建最佳拟合线，以便我们可以获得所有特定误差的总和，并且它应该是最小的。这就是为什么我们以这种特定的方式采用这个成本函数。hθ(x)^i是我的预测点。y ^i是我的真值点/真实输出。当我们进行减法时，我们可以在这里得到误差值。

        我们进行平方的原因是因为我们使用的成本函数技术是均方误差。是否存在不同类型的成本函数？是的，有平均绝对误差（MAE）和均方根误差（RMSE）。

        θ0表示截距，θ1表示斜率。_ 您只需要不断更改 θ0 和 θ1 值，并尝试找出误差最小的最佳拟合线。

        那么直线方程是什么呢

hθ(x)=θ0+θ1x

        由此，我将在二维图中解释所有这些，以便更好地理解这个理论。所以我假设我的θ0 = 0。那么我的截距将为零，最佳拟合线将穿过原点。现在我可以像这样创建我的方程。

hθ(x)= θ1x  : because my θ0 = 0

        我将使用这个方程来获取 hθ(x) 的值。让我们考虑这是我的整个数据集，我正在尝试创建一条最佳拟合线并找到该线的最小误差。

        示例数据集

        让我们绘制这些数据的图表。现在我将使用上面的方程来绘制我的最佳拟合线。

        与实际值的图表

        现在我的斜率是 θ1 ，我们假设θ1= 1。稍后，我们将改变斜率以获得不同的最佳拟合线以最小化误差。

hθ(x)= θ1x
Let θ1 = 1 (This is my slope value. Assumption this value equals to 1)
Now according to the x values in the data hθ(x) values should be like this,
x =  1 -> hθ(x) =  1 
x =  2->  hθ(x) =  2
x =  3->  hθ(x) =  3

现在我们可以用这些值绘制最佳拟合线，这条线将穿过原点（x = 0，y = 0）。

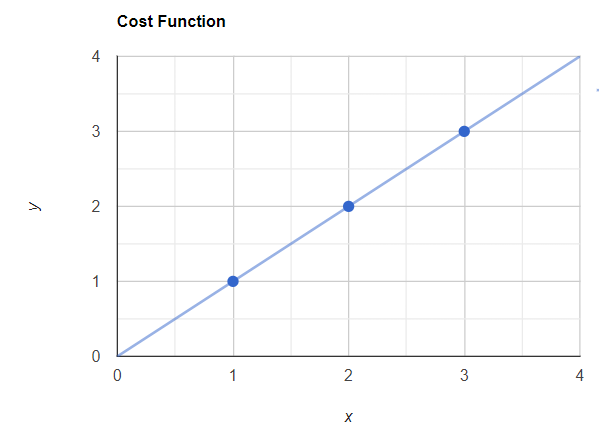
具有实际值和最佳拟合线的图表

现在你可以看到我的预测点和真实点是重叠的。现在让我们应用这个成本函数。

Here we assume like θ0 = 0 and the J(θ0, θ1) will be J(θ1) 
Now in the dataset I have 3 points. So that m will be 3. m=3
Now the summation of i =1 to 3 means the entire summation of 1,2 and 3 value.
So I will get the value by expanding this values like this,J(θ1) =  1/2*3 [All 3 dataset Sum (predicted value - actual true value)^2]
J(θ1) =  1/2*3 [ (1 -1)^2 + (2 - 2)^2 + (3 - 3)^2}
J(θ1) = 0

现在您知道 J(θ1) = 0，这意味着没有错误。这是正确的，因为显然没有错误，因为最佳拟合线通过了所有真实点。

让我们将斜率值更改为 0.5。

hθ(x)= θ1x
Let θ1 = 0.5(This is my slope value. Assumption this value equals to 0.5)
Now according to the x values in the data hθ(x) values should be like this,
x =  1 -> hθ(x) =  0.5
x =  2->  hθ(x) =  1
x =  3->  hθ(x) =  1.5

现在我们可以用这些值绘制最佳拟合线，这条线将穿过原点（x = 0，y = 0）。

所以这里红点是我的预测点，蓝点是我的实际点。现在让我们使用 J(θ1) 计算误差值。

Here we assume like θ0 = 0 and the J(θ0, θ1) will be J(θ1) 
Now in the dataset I have 3 points. So that m will be 3. m=3
Now the summation of i =1 to 3 means the entire summation of 1,2 and 3 value.
So I will get the value by expanding this values like this,J(θ1) =  1/2*3 [All 3 dataset Sum (predicted value - actual true value)^2]
J(θ1) =  1/2*3 [ (0.5 -1)^2 + (1 - 2)^2 + (1.5 - 3)^2}
J(θ1) = 1/2*3 [ (-0.5)^2 + (-1)^2 + (-1.5)^2}
J(θ1) = 0.58

现在我的 J(θ1) 值（误差）是 0.58。与之前的值相比，这是一个更大的值。

让我们将斜率值更改为0。

hθ(x)= θ1x
Let θ1 = 0(This is my slope value. Assumption this value equals to 0)
Now according to the x values in the data hθ(x) values should be like this,
x =  1 -> hθ(x) =  0
x =  2->  hθ(x) =  0
x =  3->  hθ(x) =  0

现在我们可以用这些值绘制最佳拟合线，这条线将穿过原点（x = 0，y = 0）。

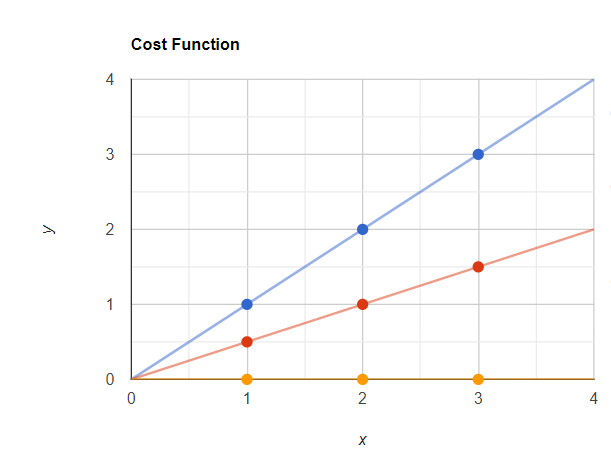
现在我的预测点为黄色，实际点为蓝色。现在让我们使用 J(θ1) 计算误差值。

Here we assume like θ0 = 0 and the J(θ0, θ1) will be J(θ1) 
Now in the dataset I have 3 points. So that m will be 3. m=3
Now the summation of i =1 to 3 means the entire summation of 1,2 and 3 value.
So I will get the value by expanding this values like this,J(θ1) =  1/2*3 [All 3 dataset Sum (predicted value - actual true value)^2]
J(θ1) =  1/2*3 [ (0 -1)^2 + (0 - 2)^2 + (0 - 3)^2}
J(θ1) = 1/2*3 [ (-1)^2 + (-2)^2 + (-3)^2}
J(θ1) = 2.3

现在让我们在图表中绘制这些 J(θ1) 值。看起来像这样，

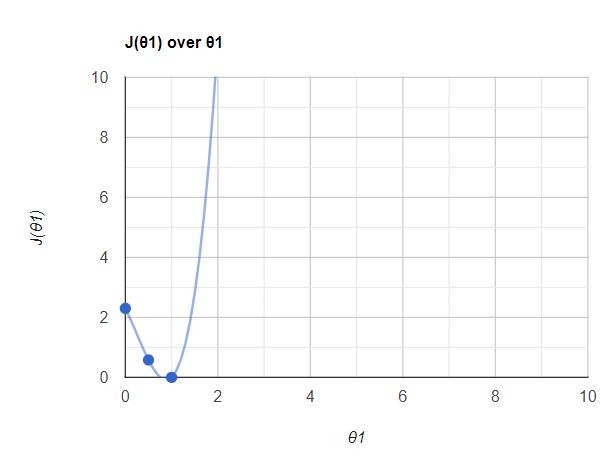
        所以这里我们使用了 3 个点，当我们使用更多的 J(θ1) 和 θ1 点来绘制时，你会得到这样的图。你知道，在 θ1 =1 点，我的误差非常低。事实上，它是零。所以我们可以说，当我们找到这个θ1值θ1= 1时，我的误差最小化了。我们将此值称为全局最小值。总体目标是通过迭代不同的θ值来最小化成本函数。成本函数的最低可能值也称为全局最小值。最终的线性回归模型将保留产生最低成本函数的 θ 值。在全局最小值中，我现在将获得最佳拟合线。

        所以这整条曲线称为梯度下降。这对于深度学习技术来说非常重要。

        所以我希望您能更好地理解简单线性回归和回归成本函数。您将在下一篇文章中了解有关收敛算法的更多信息。