Course1-Week1:机器学习简介
文章目录
- Course1-Week1:机器学习简介
- 1. 课程简介
- 1.1 课程大纲
- 1.2 Optional Lab的使用 (Jupyter Notebooks)
- 1.3 欢迎参加《机器学习》课程
- 2. 机器学习简介
- 2.1 机器学习定义
- 2.2 有监督学习
- 2.3 无监督学习
- 3. 线性回归模型
- 3.1 线性回归模型
- 3.2 代价函数
- 4. 梯度下降法
- 4.1 梯度下降法
- 4.2 用于线性回归的梯度下降
- 笔记主要参考B站视频“(强推|双字)2022吴恩达机器学习Deeplearning.ai课程”。
- 该课程在Course上的页面:Machine Learning 专项课程
- 课程资料:“UP主提供资料(Github)”、或者“我的下载(百度网盘)”。
好文:
- 2023吴恩达机器学习: 上班族35 天学完~学习笔记 (1.1 监督学习)——系列文章
- 入门机器学习/深度学习要多长时间?
1. 课程简介
1.1 课程大纲

和国内大部分课程结构不同,本套机器学习课程分为3个Course,每个Course又分为若干个Week,如上图所示。笔记的结构与课程大纲相同,由于每个Week中又包含10~20节不等的讲解视频,所以单篇笔记就包含单个Week的内容。本篇笔记就对应了课程的Course1-Week1(上图中深紫色)。
1.2 Optional Lab的使用 (Jupyter Notebooks)
为了帮助同学们在学习过程中更直观的理解机器学习中的概念,本套课程同步包含一系列实验。这些实验无需初学者有什么数学或代码基础,但需要使用 “Jupyter Notebooks” 打开。Jupyter Notebooks 是当今机器学习和数据科学从业者最广泛使用的工具,是进行编写代码、实验、尝试的默认环境。所以为了使用这些课程资料,需要我们在自己的浏览器中搭建 Jupyter Notebooks 环境,并用来测试一些想法。下面是配置环境(安装Anaconda)、打开课程资料的方法:
- 配置Jupyter Notebook环境:参考“辅助笔记-Jupyter Notebook的安装和使用”。
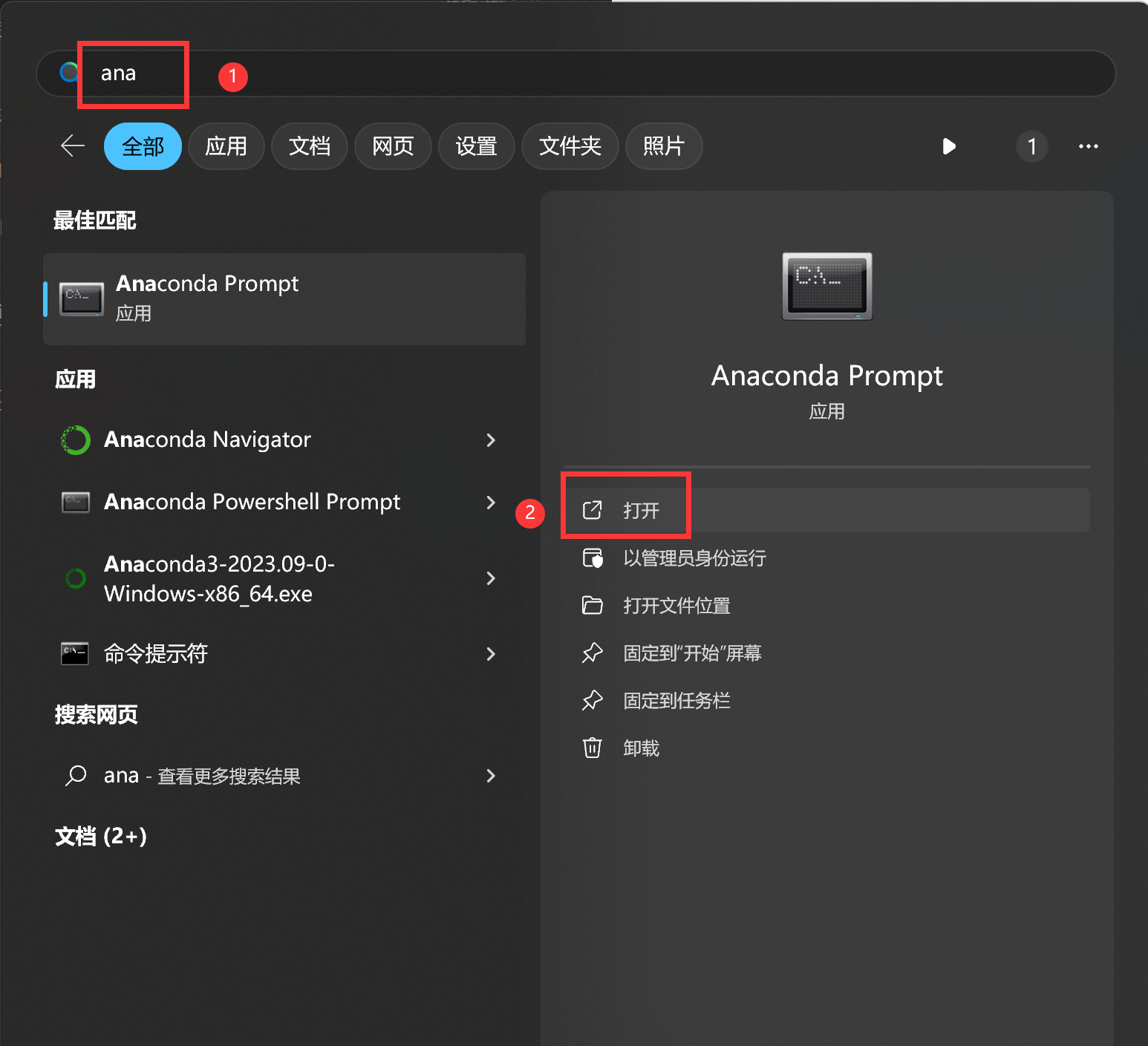
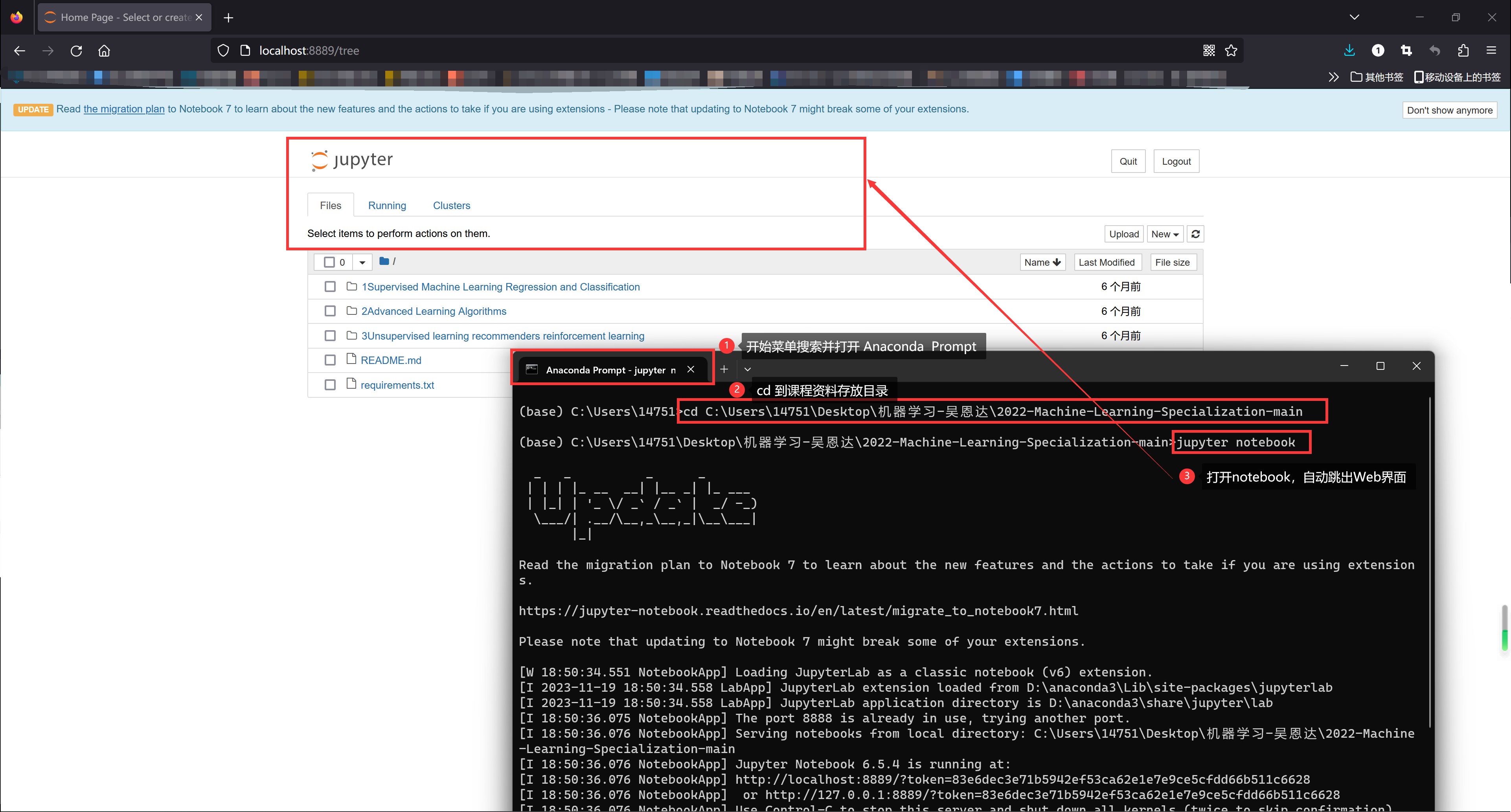
- 打开课程资料(如下图):使用“Anaconda Prompt”
cd到存放课程资料的目录,然后jupyter notebook打开即可。注1:课程资料下载见“UP主提供资料(Github)”、或者“我的下载(百度网盘)”。
注2:课程资料中包含课程中的实验、Quiz、PPT,可自行查阅。
1.3 欢迎参加《机器学习》课程
机器学习是一门让计算机在 没有明确编程 的情况下学习的科学。机器学习已经出现在生活的方方面面:
- 消费者应用领域:
- 搜索引擎的排名机制。
- 社交软件为图片添加标签。
- 流媒体服务推荐机制,比如B站的“首页通知书”。
- 语音助手返回的答案,如问Siri附近的餐厅有哪些。
- 邮箱自动识别垃圾邮件。
- 工业领域:
- 优化风力涡轮机发电。
- AI医学影像诊断。
- Landing AI将计算机视觉应用到工厂中,帮助检查流水线产品质量等。
机器学习广泛应用的原因:
- 很多场景无法写出显式程序。大多数情况下,我们不知道如何编写显式程序执行更有趣的事情,如网络引擎的推荐结果、识别人类语言、医学诊断、自动驾驶。我们所知道的唯一做这些事情的方法就是让机器学会自己做。
- AGI(Artifical General Intelligence, 通用人工智能)的创造应该要用到某种“学习算法”。通俗来说,AGI就是一个和正常人类智力相当的人工智能。“AGI”这种概念令广大AI研究者兴奋,虽然预计大概还需要50~500年才能实现,但大多数AI研究者认为最接近该目标的方法就是使用某种“学习算法(learning algorithms)”,虽然可能需要深入研究人类大脑的工作方式来寻找灵感,但机器学习算是进入AI领域的第一步。
注:学习算法(learning algorithm),是机器学习算法、深度学习算法等具备学习能力的算法的统称。
本门课程广泛介绍了现代机器学习,包括监督学习(多元线性回归、逻辑回归、神经网络和决策树)、无监督学习(聚类、降维、推荐系统)以及人工智能和机器学习创新(评估和调整模型、采用以数据为中心的方法来提高性能等)在硅谷的最佳实践。具体将:
- 使用流行的机器学习库 NumPy 和 scikit-learn 在 Python 中构建机器学习模型。
- 构建和训练用于预测和二元分类任务的监督机器学习模型,包括线性回归和逻辑回归。
2. 机器学习简介
2.1 机器学习定义
Arthur Samuel 在1950s就编写出了可以进行自我学习的跳棋程序(checkers playering program)。下面是他给出的“机器学习”的定义(非正式定义):
英文:Field of study that gives computers the ability to learn without being explicitly programmed. – Arthur Samuel (1959)
翻译:使计算机能够在没有明确编程的情况下学习的研究领域。
Question:
If the checkers program(跳棋程序) had been allowed to play only ten games (instead of tens of thousands) against itself, a much smaller number of games, how would this have affected its performance?
× Would have made it better
√ Would have made it worse启示:一般情况下,学习的机会越多,算法的表现越好。
本节课将学习很多机器学习算法,内容包括:
- 有监督学习(Supervised learning):实际应用中,有监督学习使用最广泛,并取得了最快速的进步和创新。Course1、Course2聚焦于有监督学习。
- 无监督学习(Unsupervised learning):Course3聚焦于无监督学习。
- 强化学习(Reinforcement learning)”:由于应用没有前两者广泛,所以本课程没有简单介绍。
- 使用“学习算法”的实用建议(很重要):“学习算法”本身只是一种工具,比工具本身更重要的是 如何正确使用这些工具。即使是某些大公司中最熟练的机器学习团队,可能也会因为最开始找错了算法方向而导致多年的成果付诸东流。所以本课程不仅会讲解机器学习算法,同时也会介绍最熟练的机器学习工程师是如何构建系统的,以及一些机器学习应用的最佳案例。
注:学习算法(Learning Algorithm),是机器学习算法、深度学习算法等具备学习能力的算法的统称。
2.2 有监督学习
“有监督学习”指的是学习从 输入 x x x(一个或多个) 映射到 输出 y y y 的算法。有监督学习算法的关键在于首先要提供正确的样本示例供算法学习,然后算法便可以针对未见过的输入,输出相应的预测结果。下面是一些有监督学习的在现实生活中的示例:
- 垃圾邮件过滤器:email --> 垃圾邮件?(0/1)
- 语音识别:语音 --> 文本
- 机器翻译:英文 --> 中文
- 广告投递:广告、用户信息 --> 用户点击?(0/1)
- 自动驾驶:图片、雷达信息 --> 其他车辆位置
- 视觉检测:手机图片 --> 有缺陷?(0/1)
“有监督学习”中两类最常见的典型问题就是 回归(Regression) 和 分类(Classification)。两者的主要区别在于:
- 回归问题:要预测的结果有无穷种可能,比如在一段范围内都有可能的数字取值。
- 分类问题:只有有限种可能的输出结果,比如前面提到的判断某个邮件是否为垃圾邮件。
注1:任何预测数字的“有监督学习”模型,就是解决所谓的“回归问题”。
注2:在“分类问题”中,输出“类别”的英文是class或category,两者可以混用。下面将给出这两个问题的示例。
回归问题示例:房价预测
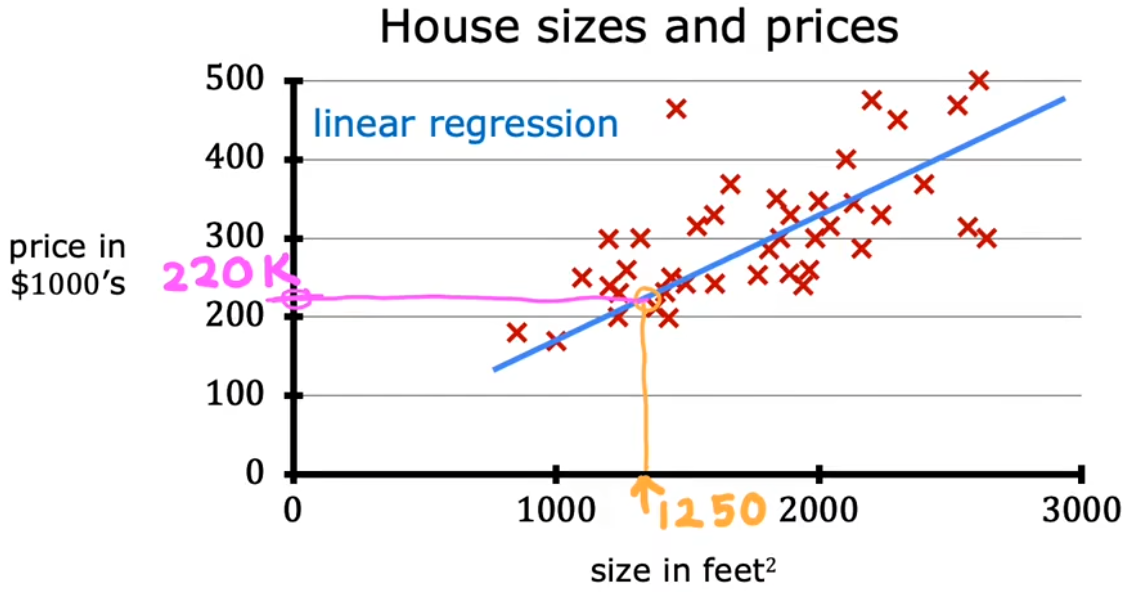
“房价预测”就是根据房子的面积计算价格。下图中的“红叉”就是预先提供的有正确映射关系的样本,“蓝色拟合线”就相当于算法学习输入样本,最后通过拟合线得到房价便是“预测”,这便是“有监督学习”的完整流程。注意到这个回归问题的输出(房价)可以是任意数字,于是便有无穷种可能。
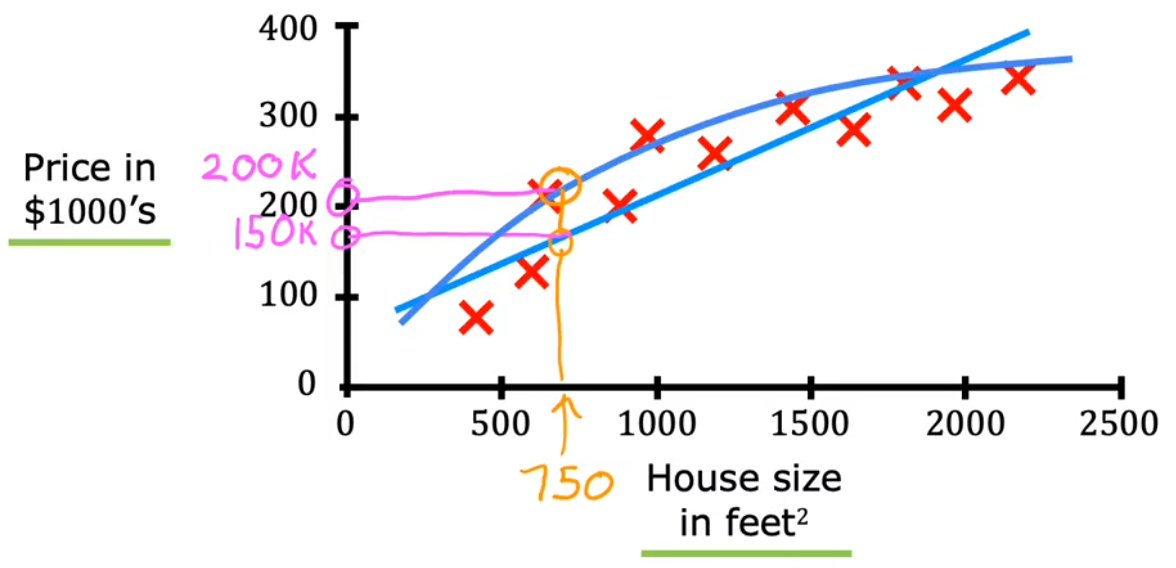
- 直线拟合:根据拟合直线,可以预测房屋面积 750 feet 2 750\text{feet}^2 750feet2 对应的价格大约为 $$150k$。
- 曲线拟合:根据拟合曲线,可以预测房屋面积 750 feet 2 750\text{feet}^2 750feet2 对应的价格大约为 $$200k$。
分类问题示例:乳腺癌检测
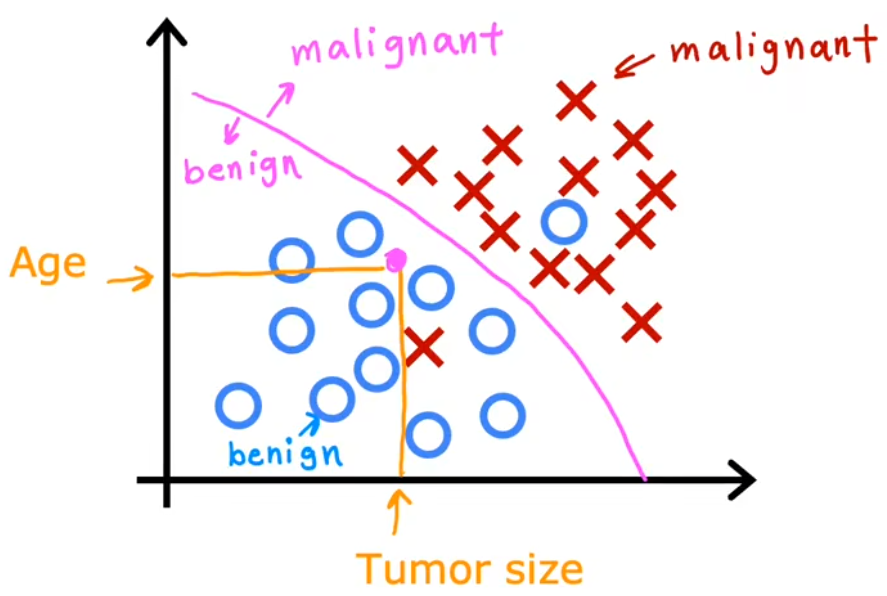
乳腺癌检测问题就是根据输入的一系列信息,如肿瘤块的大小、患者年龄、肿瘤块的厚度、细胞大小的均匀性、细胞形状的均匀性等,来判断是否为恶性肿瘤(0表示良性/1表示恶性)。下面给出“单输入的乳腺癌检测”、“两输入的乳腺癌检测”示意图:
单输入的乳腺癌检测:输入是“肿瘤的大小”,输出是“良性”、“恶性-类型1”、“恶性-类型2”。
两输入的乳腺癌检测:输入是“肿瘤的大小”、“患者年龄”,输出是“良性”、“恶性”。

2.3 无监督学习
无监督学习:
Data only comes with inputs x x x, but not output labels y y y. Algorithm has to find structure in the data.
在“有监督学习”之后,“无监督学习”也被广泛应用起来。“无监督学习”不是要找映射关系,而是想要从 没有标记的数据集 中发现一些有趣的东西,比如这个数据集中有什么 可能的模式或结构。无监督学习的主要类型有:
- 聚类(Clustering):将相似的数据点分成一组。
- 异常检测(Anomaly detection):。有非常多的应用,比如在金融系统的诈骗检测中,异常时间、异常交易可能是欺诈。
- 降维(Dimensionality reduction):在尽可能丢失少的信息的前提下,将大数据集压缩成小得多的数据集。
Question:
Of the following examples, which would you address using an unsupervised learning algorithm?
× Given email labeled as spam/not spam, learn a spam filter.
√ Given a set of news articles found on the web, group them into sets of articles about the same story.
√ Given a database of customer data, automatically discover market segments and group customers into different market segments.
× Given a dataset of patients diagnosed as either having diabetes or not, learn to classify new patients as having diabetes or not.知识点:有监督学习给数据和标签,重点在于对新输入预测出标签;无监督学习只给数据,重点在于自行分组。
下面给出“聚类”的3个示例,后续会再介绍“异常检测”和“降维”这两种无监督学习的示例:
聚类算法示例1:新闻分类
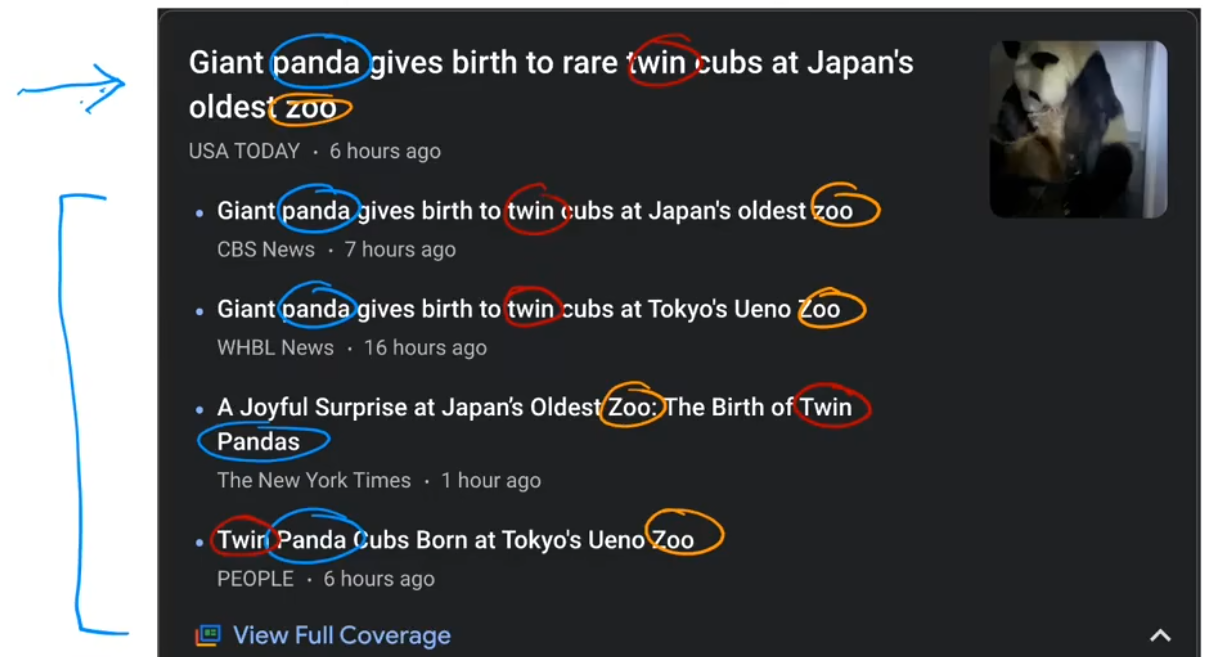
“谷歌新闻”的任务就是将每天数十万的新闻进行聚类,找到提到相似词的文章并将其分组。很酷的是,聚类算法可以自己计算出哪些词暗示了这些文章属于同一个组,并且谷歌新闻的员工也没有事先告诉算法有哪些组。如下图所示,panda、twin、zoo都是相似的词,这些文章被归为一类。
聚类算法示例2:基因分类
下图所示的基因图谱,每一列表示一个人的全部基因,每一行表示一种基因,不同的颜色表示该基因的活跃程度,这些基因包括瞳孔颜色、身高、不爱吃西蓝花/包菜/莴苣等。聚类算法仅根据这些基因数据,将人进行分组,进而找出“基因上很相似的人”。

聚类算法示例3:客户分群
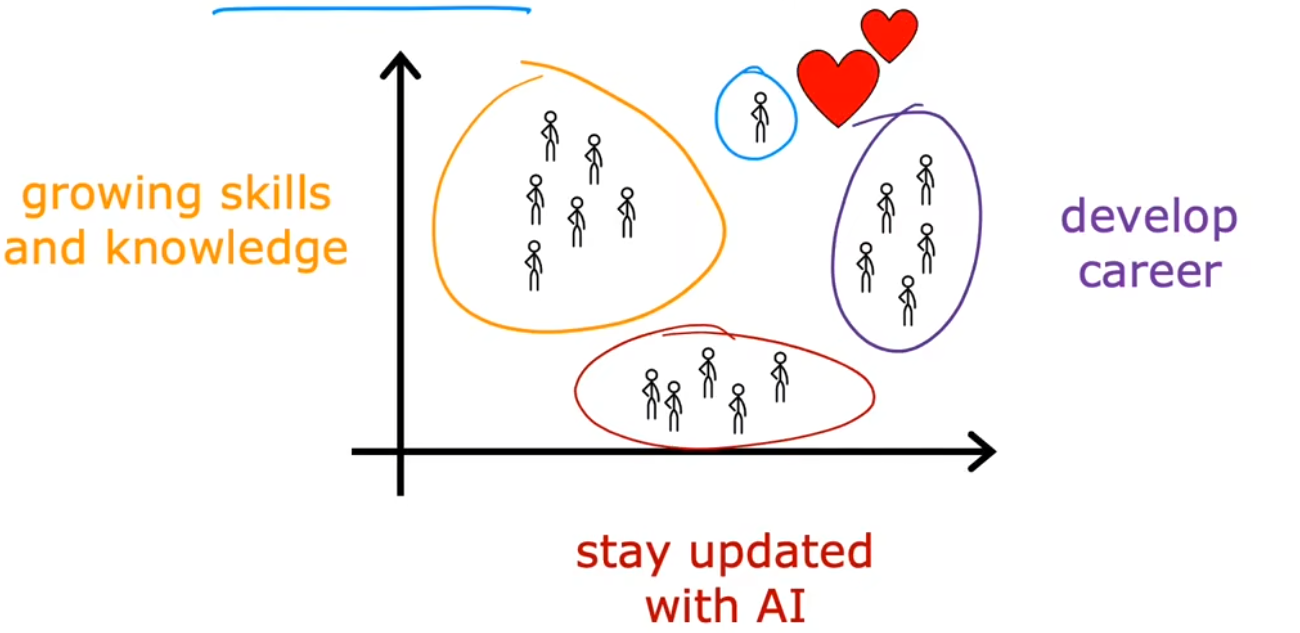
还有一个很常见的聚类算法示例就是,根据客户信息数据库,将不同的客户划分进不同的细分市场,以便更有效的服务客户。比如深度学习团队“dot AI” 想知道 dot AI社区 中的人们,参加课程、订阅通知、参加AI活动等的动机是什么。于是通过调研团队便发现了拥有不同动机的人,比如:提升技能、发展事业、紧随AI潮流、或者哪个都不是。这个例子中调研团队就相当于无监督学习算法。
本节Quiz:
- Which are the two common types of supervised learning? (Choose two)
A.Classification √
B.Clustering
C.Regression √- Which of these is a type of unsupervised learning?
A.Regression
B.Classification
C.Clustering √
3. 线性回归模型
3.1 线性回归模型
本节将通过“线性回归模型”(Linear Regression Model)介绍“有监督学习”的整个过程,这也是本课程的第一个模型。下面是常用的机器学习术语:
- Training Set(数据集):用于训练模型的数据集。
- x x x:input variable(输入变量) / feature(特征) / input feature(输入特征),也就是“特征值”。
- y y y:output variable(输出变量) / target variable(目标变量),也就是“目标值”。
- m m m:表示训练样本的数量。
- ( x , y ) (x,y) (x,y):单个训练样本。
- ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)):第 i i i 个训练样本。上标加括号是为了和求幂次区别开来。
- y ^ \hat{y} y^:表示对 y y y 的估计或预测。
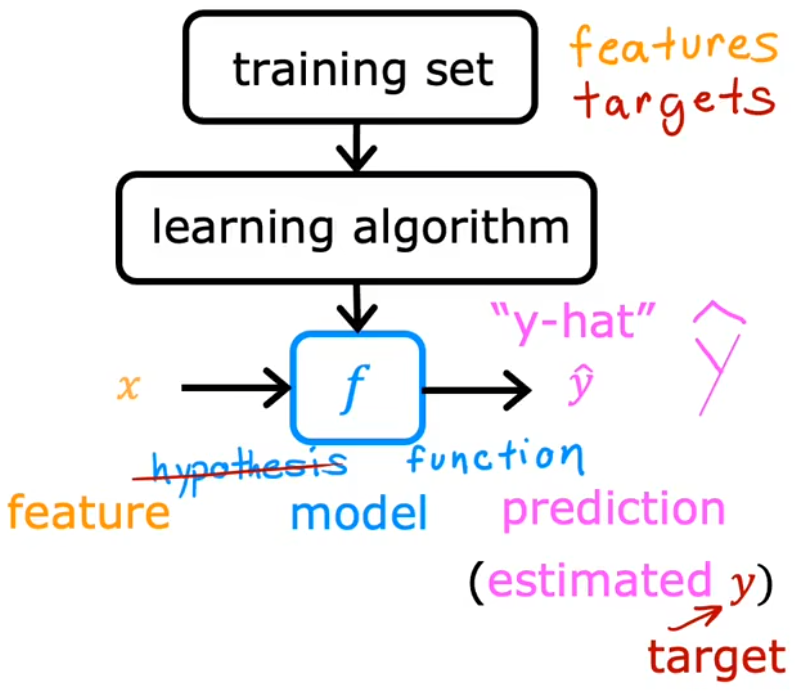
- 以前把 f f f 叫做hypothesis(假设),但是老师不建议这种叫法,而是称之为function(函数)。
上图给出了整个“有监督学习”的流程,也就是“learning algorithm”根据输入的“训练集”得到一个 函数模型 f f f,于是便可以通过 f f f 来对 输入 x x x 进行预测 输出 y ^ \hat{y} y^。而“线性回归模型”就是假设 函数模型 f f f 为一条直线,因为简单易用,这可能是世界上使用最广泛的学习算法,后续也会在其他机器学习模型中见到线性回归模型。
“线性回归”只是解决回归问题的方法之一,其他方法会在Course2中会介绍。现在以上一小节“房价预测”问题举例,若使用“线性回归模型”假设 f f f 就是一条直线,于是该模型就可以写成
f w , b ( x ) = w x + b f_{w,b}(x)=wx+b fw,b(x)=wx+b
表示函数 f f f 以 x x x 为函数输入,其输出 y ^ \hat{y} y^ 取决于 w w w 和 b b b 的值。
- w w w、 b b b:模型的参数(parameter)。
- f w , b ( x ) f_{w,b}(x) fw,b(x)通常会简写为 f ( x ) f(x) f(x)。
3.2 代价函数
显然,虽然现在已经构建好了“线性回归模型”,但是过训练集的直线有无数种,如何找出 与训练数据最拟合的线 还不明确,于是本节就来介绍 代价函数(cost funtion)。在机器学习中,代价函数用于 衡量模型的好坏,最简单、最常用的代价函数是“平均误差代价函数”(Squared error cost function):
J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 \begin{aligned} J(w,b) &= \frac{1}{2m} \sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)})^2\\ &= \frac{1}{2m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^2 \end{aligned} J(w,b)=2m1i=1∑m(y^(i)−y(i))2=2m1i=1∑m(fw,b(x(i))−y(i))2
- w w w、 b b b:模型的参数。
- i i i:训练样本的标号。
- m m m:训练样本的总数。
- y ( i ) y^{(i)} y(i):第 i i i 的样本的真实目标值。
- y ^ ( i ) \hat{y}^{(i)} y^(i):对 y ( i ) y^{(i)} y(i) 的预测目标值。
- 除以 2 m 2m 2m:按照惯例,机器学习中的平均代价函数会除以 2 m 2m 2m 而非 m m m,这是为了使后续的计算更加简洁。
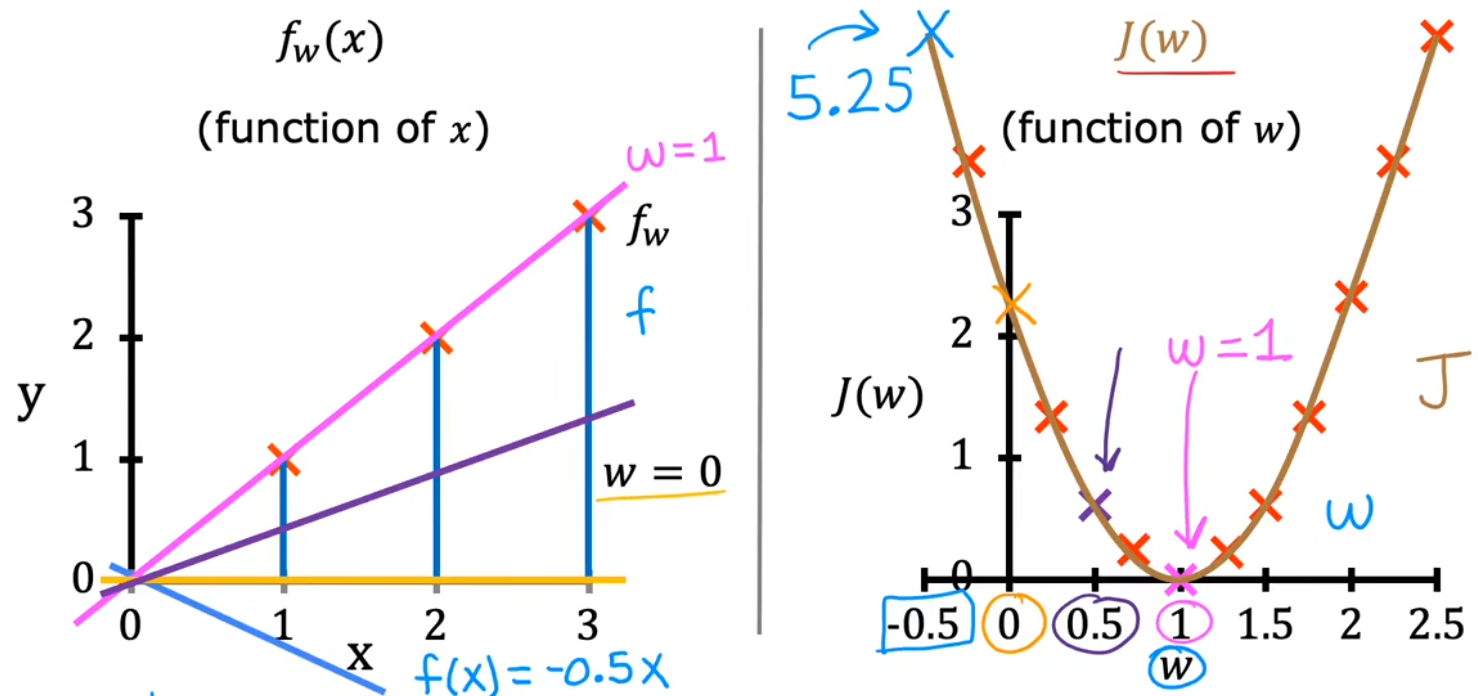
现在来直观的看一下,最小化代价函数如何找到与训练数据最拟合的线。首先简化模型,设置参数 b = 0 b=0 b=0,并假设训练数据只有三个点。下图给出了不同的 w w w 所对应不同的 代价 J ( w ) J(w) J(w),显然在 w = 1 w=1 w=1 处代价最小,直线也最拟合:
min w J ( w ) = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( w x ( i ) − y ( i ) ) 2 \begin{aligned} \min_{w} J(w) &= \frac{1}{2m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^2\\ &= \frac{1}{2m} \sum_{i=1}^{m}(wx^{(i)}-y^{(i)})^2 \end{aligned} wminJ(w)=2m1i=1∑m(fw,b(x(i))−y(i))2=2m1i=1∑m(wx(i)−y(i))2
那回到刚才的问题中,同时将 w w w和 b b b 都考虑在内,并引入更多的训练数据,便可以得到下面的代价函数示意图。为了更好的将代价函数可视化,同时使用“等高线图”和“3D图”来展示不同的 w w w和 b b b 所对应不同的 代价 J ( w , b ) J(w,b) J(w,b)。“3D图”类似一个“碗”,显然在“碗”的底部,代价函数最小:
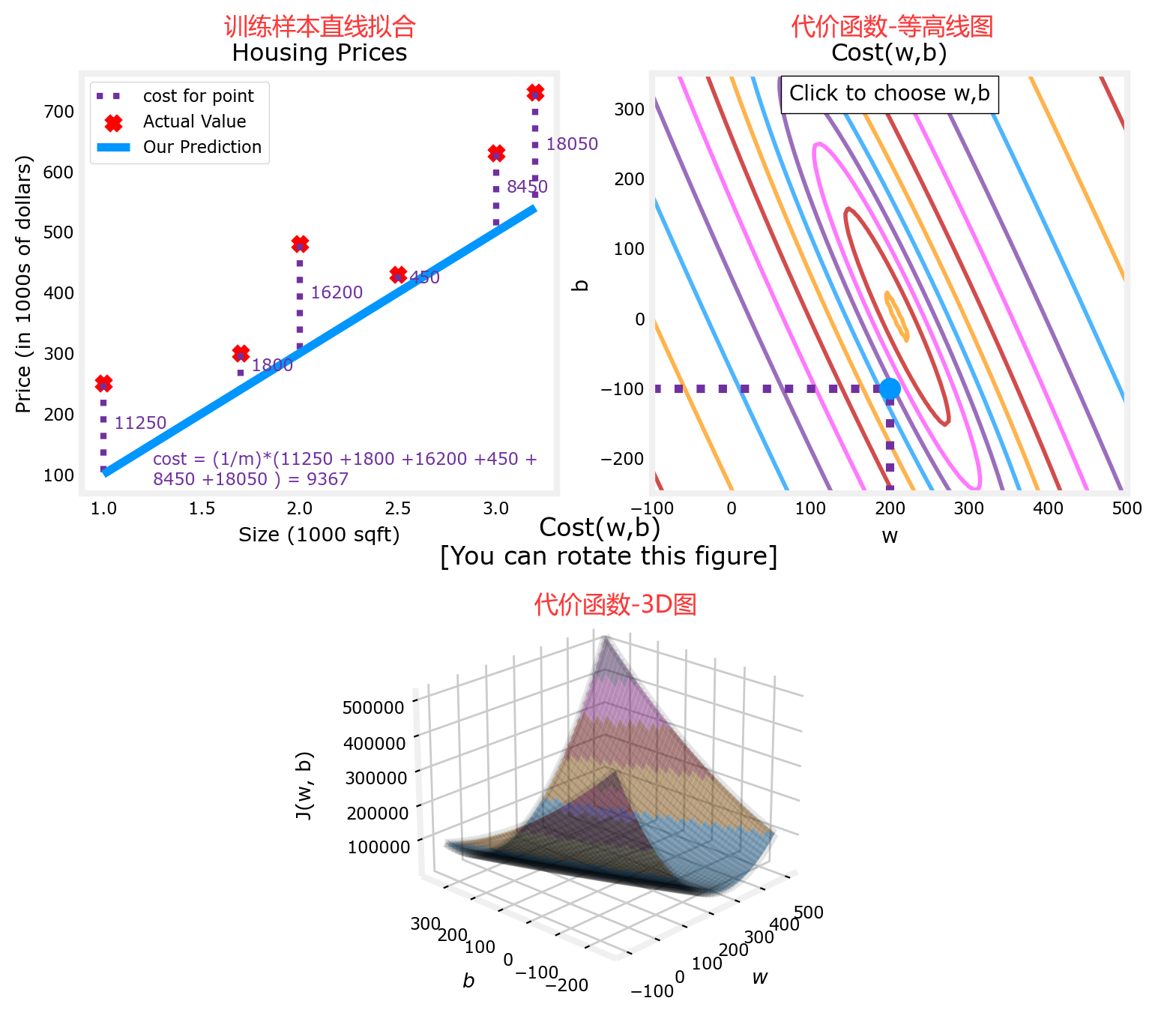
上图见课程资料:C1_W1_Lab04_Cost_function_Soln.ipynb
- bug1:ModuleNotFoundError: No module named ‘ipympl’
解决办法:新打开一个“Anaconda Prompt”输入conda install ipympl,然后重启内核重新运行即可。注:图片很多,运行后会有点卡,若加载不出来图片可以尝试重新运行。
本节Quiz:
- For linear regression, the model is f w , b ( x ) = w x + b f_{w,b}(x)= wx + b fw,b(x)=wx+b. Which of the following are the inputs, or features, that are fed into the model and with which the model is expected to make a prediction?
× m m m
× ( x , y ) (x,y) (x,y)
√ x x x
× w w w and b b b.- For linear regression, if you find parameters w w w and b b b so that J ( w , b ) J(w, b) J(w,b) is very close to zero, what can you conclude?
× This is never possible - there must be a bug in the code.
√ The selected values of the parameters w w w and b b b cause the algorithm to fit the training set > really well.
× The selected values of the parameters w w w and b b b cause the algorithm to fit the training set > really poorly.
虽然现在距离完成“线性回归问题”非常接近了,但是上述是通过人眼来直观的寻找代价函数的最小点,实际上要画出有足够多细节的3D图需要计算大量的 J ( w , b ) J(w,b) J(w,b),而很多 J ( w , b ) J(w,b) J(w,b)点 都是没用的,这显然不划算。下一节就来介绍如何通过计算有限的 J ( w , b ) J(w,b) J(w,b)点 来找到代价函数最小点。
4. 梯度下降法
4.1 梯度下降法
梯度下降(Gradient Desent)常用于寻找某函数(比如代价函数)的最大值、最小值。梯度下降不仅用于线性拟合,也用于训练如神经网络(Course2)等深度学习模型、以及一些最大型、最复杂的人工智能模型。下面以前面的 min w , b J ( w , b ) \min_{w,b} J(w,b) minw,bJ(w,b) 来举例,梯度下降算法的步骤为:
- 选择初始点,一般在取值范围内选取简单的整数,如 w = 1 , b = 0 w=1,b=0 w=1,b=0。
- 沿着 J J J 的“负梯度”方向,不断迭代计算 w w w、 b b b。之所以沿着“负梯度”方向,是因为沿该方向下降速度最快(steepest descent, 最速下降)。如下:
w = w − α ∂ ∂ w J ( w , b ) b = b − α ∂ ∂ b J ( w , b ) \begin{aligned} w &= w - \alpha \frac{\partial }{\partial w} J(w,b)\\ b &= b - \alpha \frac{\partial }{\partial b} J(w,b) \end{aligned} wb=w−α∂w∂J(w,b)=b−α∂b∂J(w,b)
- α \alpha α:学习率(Learning rate),用于控制步长。通常为介于0~1之间的一个小的正数,如0.01。
- ∂ ∂ w J ( w , b ) \frac{\partial }{\partial w} J(w,b) ∂w∂J(w,b):代价函数对 w w w 的偏导数(Partial Derivative),其取负值表明的方向可以使 J J J 下降。
- ∂ ∂ b J ( w , b ) \frac{\partial }{\partial b} J(w,b) ∂b∂J(w,b):代价函数对 b b b 的偏导数,意义同上。
注意:上面是 同时更新(Simultaneously update),也就是使用旧的 ( w , b ) (w,b) (w,b) 直接分别计算出新的 w w w、 b b b;而不是先更新 w w w,再使用这个新的 w w w 计算新的 b b b。
- 直到 w w w和 b b b的负梯度 都为 0 0 0(或者 0 0 0的邻域内),即可认为找到 J J J 的最低点。
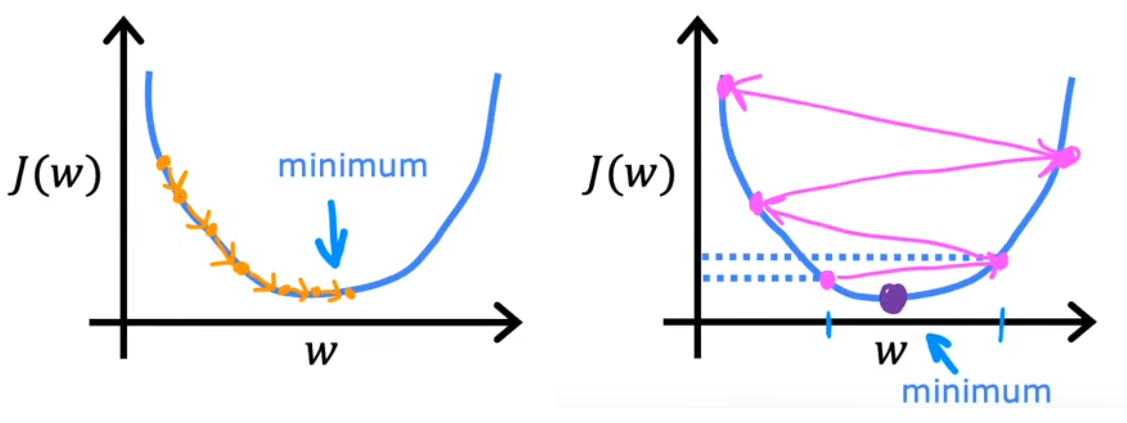
下面两张图很直观的给出了整个梯度下降法的过程。在下左图中,首先固定 b = 0 b=0 b=0,只分析 w w w 对代价函数 J ( w ) J(w) J(w) 的影响。可以发现,若当前 w w w在最低点右侧,由于“负梯度”小于0,于是下一个 w w w将向左移动;反之若当前 w w w在最低点左侧,由于“负梯度”大于0,下一个 w w w将向右迭代。只要选择合适的学习率 α \alpha α,最终就可以找到最低点所在的 w w w。在下右图中,则进一步同时考虑 w w w和 b b b,可以发现每次也是沿着“负梯度”下降最快的方向,最终可以到达最低点所在处。这个迭代的过程就是“梯度下降”,类似于“下山”的过程。

注意点1:学习率
学习率 α \alpha α 的选取将会对梯度下降的效率产生巨大影响。若 α \alpha α 选取的不好,甚至会导致无法实现梯度下降。
- α \alpha α 选取的太小,会导致下降的速度非常慢(意味着需要计算很长时间),但最终也会收敛(converge)到最小值。
- α \alpha α 选取的太大,很可能会导致在极值点附近反复横跳甚至越来越远,也就是不会收敛甚至发散(diverge)。
- α \alpha α 选取的合适,越接近代价函数极小值,梯度越来越小,就会导致步长越来越小。

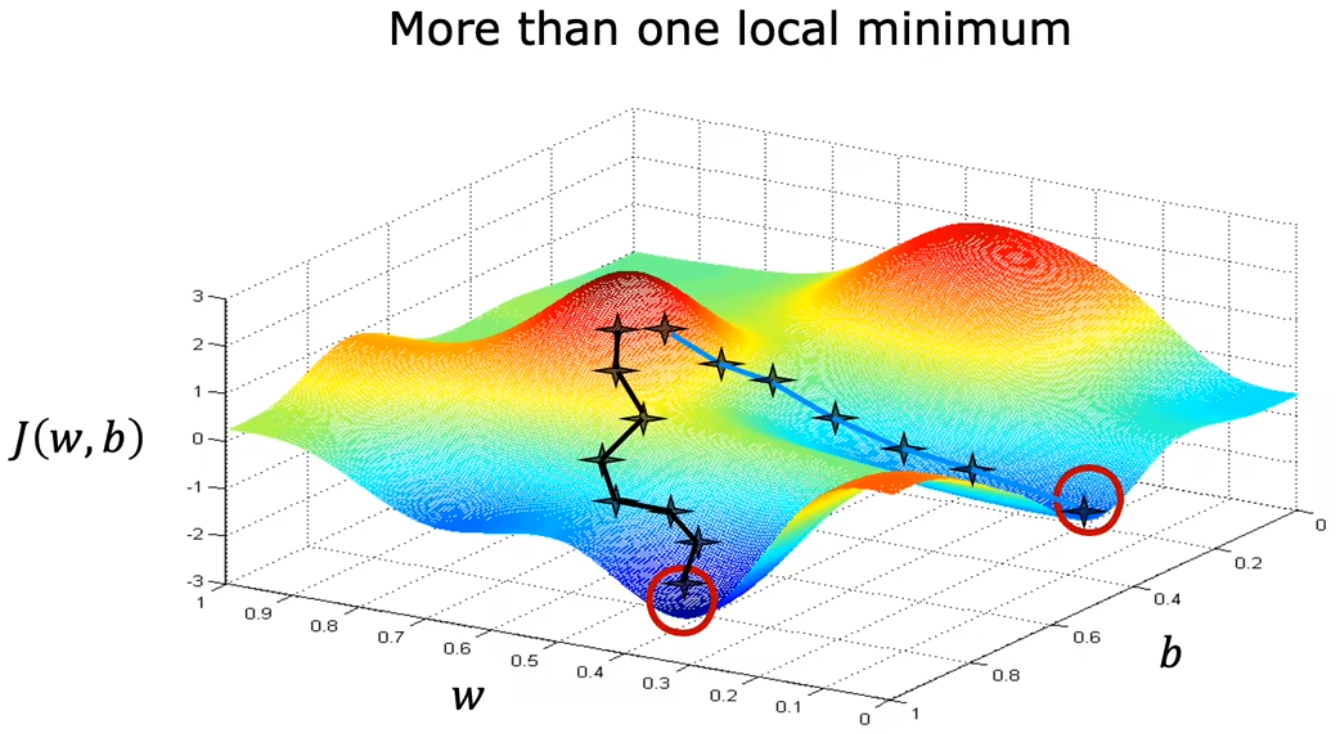
注意点2:多个极值点
在前面的讨论中,一直使用平方误差项作为代价函数。对于 平方误差项 的代价函数,都是“凸函数”或“凸面”。但若代价函数非凸时,可能就会存在不止一个极值。如上图1-1-13中,不同的起始点,就会导致不同的收敛速度或极值。所以 代价函数尽量要选择凸函数。
4.2 用于线性回归的梯度下降
介绍完梯度下降法,现在来总结一下,将前面的线性回归模型、代价函数、梯度下降算法结合起来,按照下面公式不断迭代直至其收敛:
Linear regression model : f w , b ( x ) = w x + b Cost function : J ( w , b ) = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 Gradient descent repeat until convergence : { w = w − α ∂ ∂ w J ( w , b ) = w − α m ∑ i = 1 m [ ( f w , b ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ] b = b − α ∂ ∂ b J ( w , b ) = b − α m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) \begin{aligned} \text{Linear regression model} &: \quad f_{w,b}(x) = wx+b\\ \text{Cost function} &: \quad J(w,b) = \frac{1}{2m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^2\\ \begin{aligned} \text{Gradient descent} \\ \text{repeat until convergence} \end{aligned} &: \left\{\begin{aligned} w &= w - \alpha \frac{\partial }{\partial w} J(w,b) = w - \frac{\alpha}{m} \sum_{i=1}^{m}[(f_{w,b}(x^{(i)})-y^{(i)})·x^{(i)}] \\ b &= b - \alpha \frac{\partial }{\partial b} J(w,b) = b - \frac{\alpha}{m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)}) \end{aligned}\right. \end{aligned} Linear regression modelCost functionGradient descentrepeat until convergence:fw,b(x)=wx+b:J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2:⎩ ⎨ ⎧wb=w−α∂w∂J(w,b)=w−mαi=1∑m[(fw,b(x(i))−y(i))⋅x(i)]=b−α∂b∂J(w,b)=b−mαi=1∑m(fw,b(x(i))−y(i))
从“等高线图”的角度来看,梯度下降法的迭代过程可能如下图红色箭头所示,从起始点不断收敛到最小值,并且注意到这个过程也是越来越慢的:
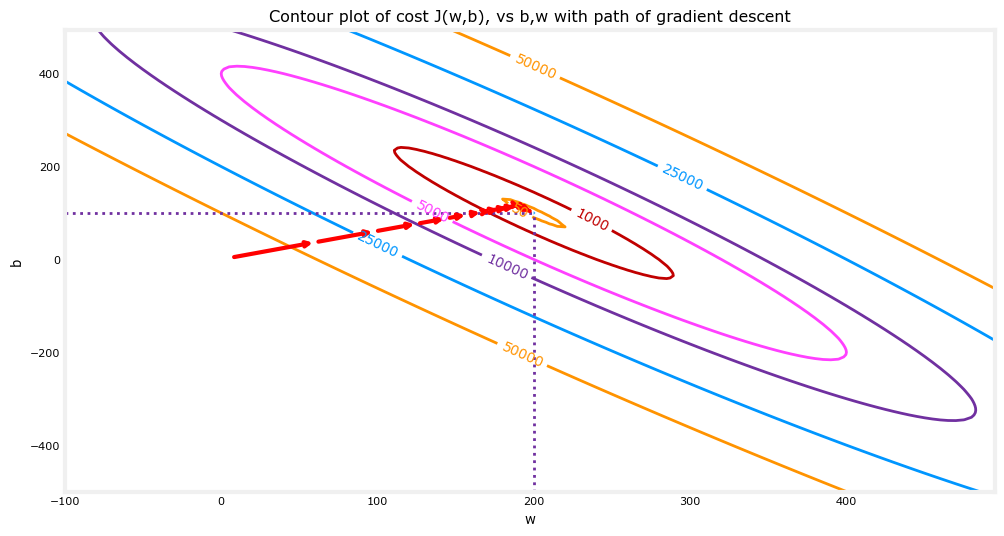
最后说明一下,由于在使用梯度下降法求解问题的过程中,每次迭代都会使用到所有的训练集数据计算代价函数及其梯度,所以这个梯度下降的过程称为“批量梯度下降(Batch gradient descent)”。当然本问题较为简单,在其他数据更为复杂的模型中,为了简化梯度下降法的计算量,每次只使用训练集的子集。
本节Quiz:
- Gradient descent is an algorithm for finding values of parameters w and b that minimize the cost function J ( w , b ) J(w,b) J(w,b).
repeat until convergence : { w = w − α ∂ ∂ w J ( w , b ) b = b − α ∂ ∂ b J ( w , b ) \text{repeat until convergence}: \left\{\begin{aligned} w &= w - \alpha \frac{\partial }{\partial w} J(w,b) \\ b &= b - \alpha \frac{\partial }{\partial b} J(w,b) \end{aligned}\right. repeat until convergence:⎩ ⎨ ⎧wb=w−α∂w∂J(w,b)=b−α∂b∂J(w,b)When ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) is a negative number (less than zero), what happens to w w w after one update step?
× w w w stays the same
× It is not possible to tell if w w w will increase or decrease.
× w w w decreases.
√ w w w increases.
- For linear regression, what is the update step for parameter b b b?
× b = b − α m ∑ i = 1 m [ ( f w , b ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ] b = b - \frac{\alpha}{m} \sum_{i=1}^{m}[(f_{w,b}(x^{(i)})-y^{(i)})·x^{(i)}] b=b−mα∑i=1m[(fw,b(x(i))−y(i))⋅x(i)]
√ b = b − α m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) b = b - \frac{\alpha}{m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)}) b=b−mα∑i=1m(fw,b(x(i))−y(i))














)




