前言

树状数组巧妙了利用位运算和树形结构实现了允许单点修改的情况下，动态维护前缀和，并且实现单点修改和前缀和查询的效率的很可观。树状数组也可以对差分数组维护前缀和来实现区间修改区间查询，但由于过于繁琐，对于区间查询往往用线段树来代替，但树状数组以其简洁的代码实现成为了动态维护前缀和的不二选择。

lowbit

在介绍树状数组前需要先了解lowbit的概念，其作用会在后面树状数组中具体解释。

lowbit的定义

非负整数n在二进制表示下最低位1以及其后面的0构成的数值

例如: 44d = 10 1100b ，那么lowbit(44) = (100)b = 4(d)

lowbit的计算

我们手算补码的时候有一个技巧就是从符号位的下一位开始一直取反，到最后一个1的时候不对其取反然后停止，因为非符号位取反加一后原先的最后一个1又会变成1，于是我们可以利用这个技巧来快速的求lowbit。

我们将x和~x + 1做与运算就会得到lowbit，因为计算机中对一个数字取反后连符号位都会取反，而一个数字取反+1后原先的最低位1以及其后面的0不受影响，所以x 和 ~x + 1的公共部分就是lowbit

故有lowbit(x) = x &(~x + 1)

即然我们说了计算机中直接取反会对符号位也取反，那么~x + 1就会得到其相反数的补码，而计算机中以补码存储数字，故上面的式子可改进为lowbit(x) = x & -x

树状数组的思想

**树状数组(Binary Indexed Tree)**既然叫树状数组，那么它是怎么将数组抽象成树形结构的呢？

其实和汉明码类似，lowbit其实就是二进制的第一位为1、第二位为1、第三位为1…

而对于1到n这n个数字我们如果取二进制表示下含lowbit（x）的数字，我们发现这些数字正好是若干个长度为lowbit(x)的连续序列组成，每个序列间的间隔也是lowbit(x)

我们按照lowbit划分层次，每层以lowbit(x) * 1 ,lowbit(x) * 2 ,lowbit(x) * 3…结尾的长度为lowbit(x)的连续序列作为该层的节点，同时我们以t[ i ]代表当前层第i个序列的元素之和

而我们要维护前缀和的原序列就成了我们的叶子节点

于是有了下图的树形结构

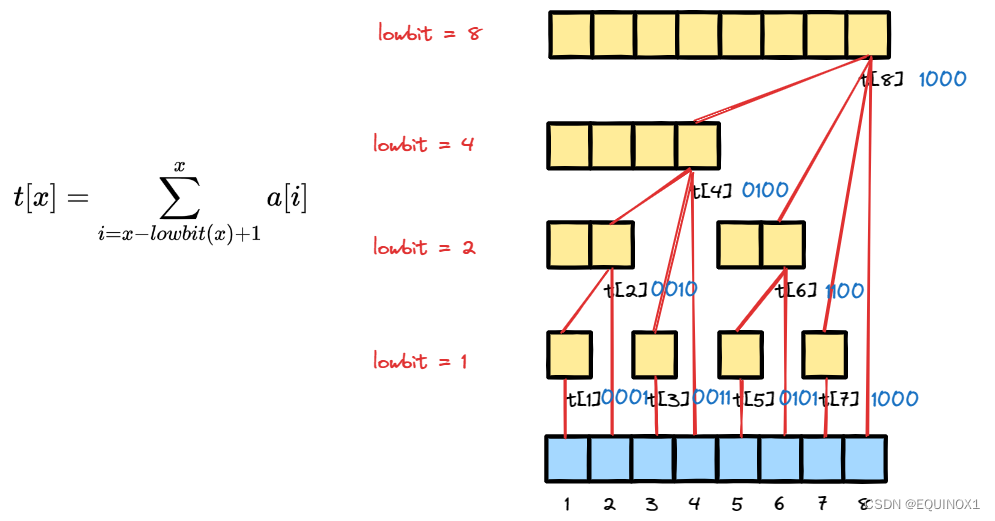
这棵树有如下特点：

• t[x]保存以x为根节点的子树中叶节点值的和
• t[x]节点的长度等于lowbit(x)
• t[x] 的父节点为t[x + lowbit[x]]
• 整棵树的深度为logn + 1
• 我们发现t[x]满足如下公式：

$$t[x]=\sum _{i=x-lowbit(x)+1}^{x}a[i]$$

树状数组的操作

由于区间修改我们有更适合的数据结构——线段树，所以我们就不介绍树状数组维护差分数组实现区间修改的操作了。

单点修改 update

当我们给一个叶子节点x增加k，那么需要对其父节点开始往上更新，而x父节点就是x + x & -x，所以一层循环就能搞定

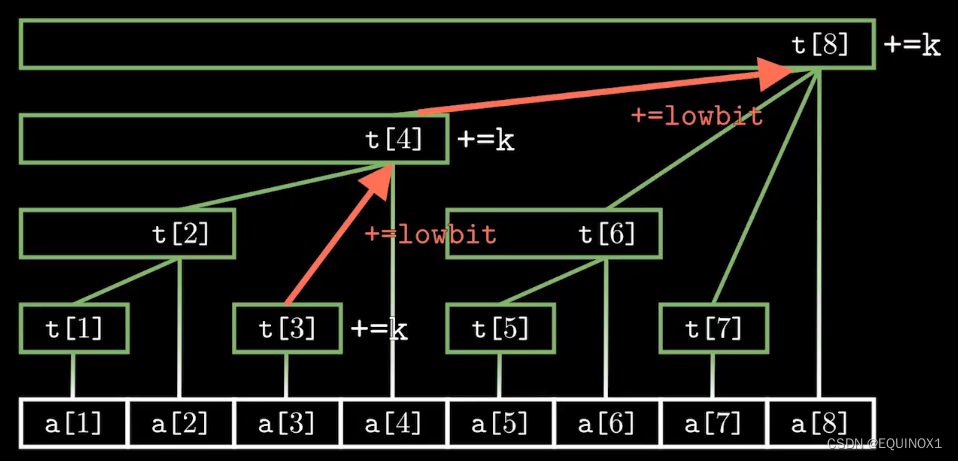
void update(int x, int k)
{for (; x <= n; x += x & -x)t[x] += k;
}

时间复杂度O(logn)

前缀查询 query

查询前x个元素的前缀和，我们从图上看发现我们只需要从t[x]往左上的第一个节点走，路径上节点的值之和就是前x个节点的前缀和

而找到左上第一个节点我们只需要减去当前节点的lowbit值即可

而减去lowbit其实就是把最低位1置为0，而把最低位1置位0我们还可以通过x &= (x - 1)来实现

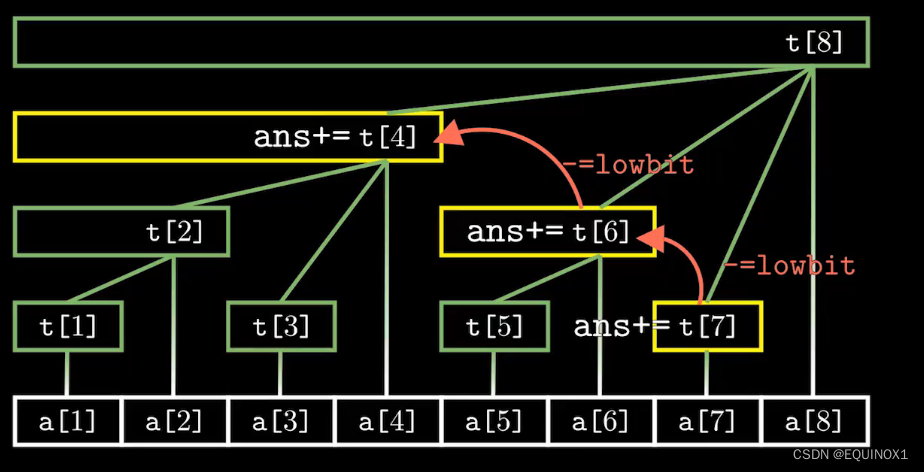
int query(int x)
{int sum = 0;for (; x > 0; x &= (x - 1))sum += t[x];return sum;
}

树状数组的建立 build

前面谈了单点修改和前缀查询，那么给定一个长度为n的数组我们如何建立树状数组呢？

暴力做法：进行n次插入操作，时间复杂度O(nlogn)

虽然可行，但是我们发现n次插入过程中其实是有冗余操作的，我们每次插入都会一直向上更新到根节点，但是我们这个过程可以等效为每次完成一个节点值的计算都对其父节点进行更新，这样最后我们的每个节点的值都是正确的，而且也只对数组遍历了一次，实现了O(n)建树

代码如下：

void build(const vector<int> &arr)
{for (int i = 1; i <= n; i++){t[i] += arr[i];t[i + (i & -i)] += t[i];}
}