友情链接：C/C++系列系统学习目录

---

🚀一、图的基本概念和术语

**概念：**在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。注意：顶点有时也称为节点或者交点，边有时也称为链接。 社交网络，每一个人就是一个顶点，互相认识的人之间通过边联系在一起, 边表示彼此的关系。这种关系可以是单向的，也可以是双向的！

树和链表都是图的特例，在线性表中，数据元素之间是被串起来的，仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继。在树形结构中，数据元素之间有着明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素相关，但只能和上一层中一个元素相关。图是一种较线性表和树更加复杂的数据结构。在图形结构中，结点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。

如果一个编程问题可以通过顶点和边表示，那么我们就可以将问题用图画出来，然后使用相应的算法来找到解决方案

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pJ0nLt8L-1690729858577)(E:\create\图片\图\1.png)]

1、有向图和无向图

3、基本图和多重图

一个图G若满足:①不存在重复边;②不存在顶点到自身的边，则称图G为简单图。上图中G1 和G2 均为简单图。数据结构中仅讨论简单图。

若图G中某两个结点之间的边数多于一条，又允许顶点通过同一条边和自己关联，则G为多重图。多重图的定义和简单图是相对的。

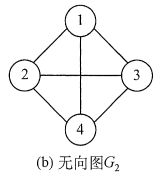
4、完全图

对于无向图，在完全图中任意两个顶点之间都存在边。

对于有向图，在有向完全图中任意两个顶点之间都存在方向相反的两条弧。

上图中G2为无向完全图，而G3为有向完全图。

5、子图

上图中G3为G1的子图。

6、连通、连通图和连通分量

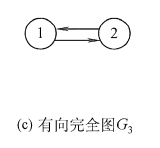
在无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的。若图G中任意两个顶点都是连通的，则称图G为连通图，否则称为非连通图。无向图中的极大连通子图称为连通分量。若一个图有n个顶点，并且边数小于n − 1，则此图必是非连通图。如下图(a)所示， 图G4有3个连通分量，如图（b）所示。

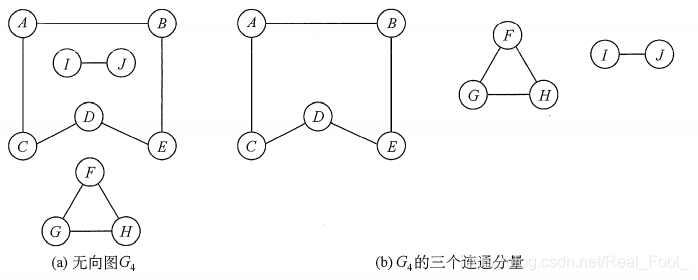
注意：弄清连通、连通图、连通分量的概念非常重要。首先要区分极大连通子图和极小连通子图，极大连通子图是无向图的连通分量，极大即要求该连通子图包含其所有的边;极小连通子图是既要保持图连通又要使得边数最少的子图。

7、强连通图、强连通分量

在有向图中，若从顶点v到顶点w和从顶点w到项点v之间都有路径,则称这两个顶点是强连通的。若图中任何一对顶点都是强连通的，则称此图为强连通图。有向图中的极大强连通子图称为有向图的强连通分量，图G1的强连通分量如下图所示。

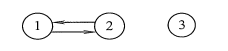
注意:强连通图、强连通分量只是针对有向图而言的。一般在无向图中讨论连通性，在有向图中考虑强连通性。

8、生成树、生成森林

连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为n,则它的生成树含有n − 1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。在非连通图中，连通分量的生成树构成了非连通图的生成森林。图G2的一个生成树如下图所示。

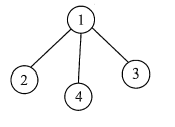
注意:包含无向图中全部顶点的极小连通子图，只有生成树满足条件，因为砍去生成树的任一条边，图将不再连通。

9、顶点的度、入度和出度

图中每个顶点的度定义为以该项点为一个端点的边的数目。

对于有向图,顶点v vv的度分为入度和出度，入度就是进来的边，出度就是出去的边

10、边的权和网

在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。这种边上带有权值的图称为带权图，也称网。

11、稠密图、稀疏图

边数很少的图称为稀疏图，反之称为稠密图。稀疏和稠密本身是模糊的概念，稀疏图和稠密图常常是相对而言的。

12、路径、路径长度和回路

顶点vp到顶点vq之间的一条路径是指它们之间的顶点序列（包括本身），当然关联的边也可以理解为路径的构成要素。路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。若一个图有n个顶点，并且有大于n − 1条边，则此图一定有环。

13、 简单路径、简单回路

在路径序列中，顶点不重复出现的路径称为简单路径。除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。

14、距离

从顶点u出发到顶点v的最短路径若存在，则此路径的长度称为从u到v的距离。若从u到v根本不存在路径，则记该距离为无穷( ∞ )。

15、有向树

一个顶点的入度为0、其余顶点的入度均为1的有向图，称为有向树。

🚀二、图的表示：邻接表

⛳（一）邻接列表原理精讲

• 在邻接列表实现中，每一个顶点会存储一个从它这里开始的相邻边的列表。比如，如果顶点 B 有一条边到 A、C 和 E，那么 B 的列表中会有 3 条边。
• 邻接列表只描述指向外部的边。B 有一条边到 A，但是 A 没有边到 B，所以 B 没有出现在 A 的邻接列表中。
• 查找两个顶点之间的边或者权重会比较费时，因为要遍历邻接列表直到找到为止。

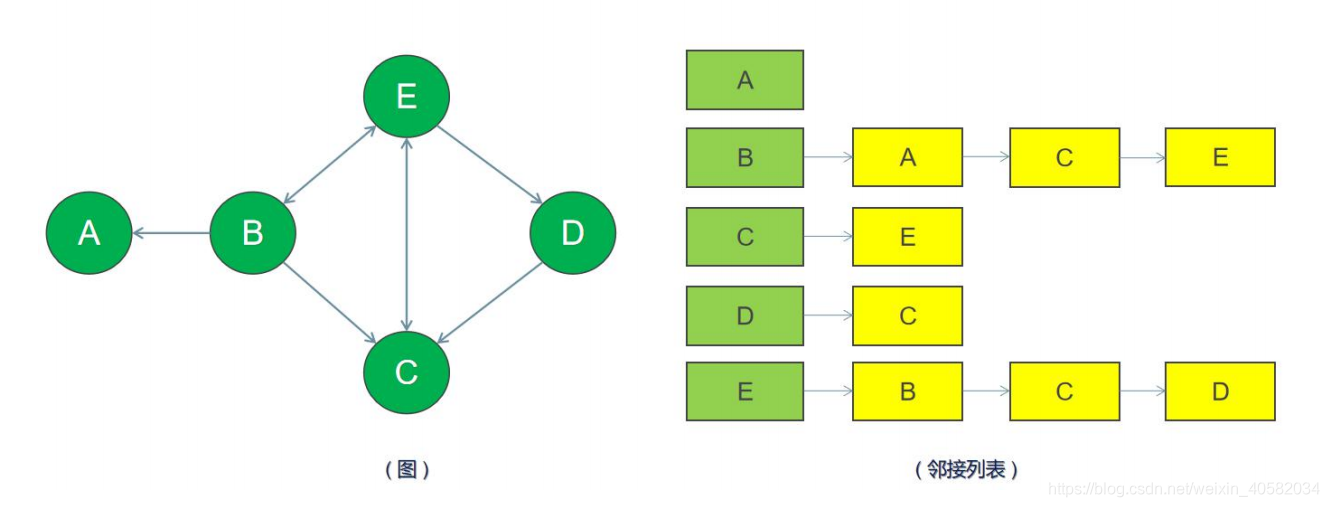
邻接矩阵：

由二维数组对应的行和列都表示顶点，由两个顶点所决定的矩阵对应元素数值表示这里两个顶点是否相连(如,0表示不相连，非0表示相连和权值)﹑如果相连这个值表示的是相连边的权重。例如，广西到北京的机票，我们用邻接矩阵表示:

• 行表示起点，列表示终点
• 往这个图中添加顶点的成本非常昂贵，因为新的矩阵结果必须重新按照新的行/列创建，然后将已有的数据复制到新的矩阵中。
• 即用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YNpfMlMW-1690729858579)(E:\create\图片\图\2.png)]

#define MaxVertexNum 100	//顶点数目的最大值
typedef char VertexType;	//顶点的数据类型
typedef int EdgeType;	//带权图中边上权值的数据类型
typedef struct{VertexType Vex[MaxVertexNum];	//顶点表EdgeType Edge[MaxVertexNum][MaxVertexNum];	//邻接矩阵，边表int vexnum, arcnum;	//图的当前顶点数和弧树
}MGraph;

比较：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OjUq1hBo-1690729858580)(E:\create\图片\图\3.png)]

结论：大多数时候，选择邻接列表是正确的。（在图比较稀疏的情况下，每一个顶点都只会和少数几个顶点相连，这种情况下邻接列表是最佳选择。如果这个图比较密集，每一个顶点都和大多数其他顶点相连，那么邻接矩阵更合适。)

⛳（二）邻接表的算法实现

顶点表结点由顶点域(data)和指向第一条邻接边的指针(firstarc) 构成，边表(邻接表)结点由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc) 构成。

1.邻接表结构的定义

#define MAXSIZE 1024typedef struct _EdgeNode//新的边
{int adjvex;//邻接的顶点 （用下标位置来表示）int weight;//权重struct _EdgeNode *next;//指向下一个顶点/边
}EdgeNode;typedef struct _VertexNode//顶点结点
{char data;//结点数据struct _EdgeNode *first; 	//指向邻接的第一条边
}VertexNode,*AdjList;typedef struct _AdJListGraph
{AdjList adjList;//顶点数组，结构体数组int numVex;int numEdg;
}AdjListGraph;

2.邻接表的初始化

bool Init(AdjListGraph &gh)
{gh.adjList = new VertexNode[MAXSIZE];//分配顶点数组地址if (!gh.adjList) return false;gh.numEdg = 0;gh.numVex = 0;}

3.邻接表的创建

//寻找顶点的数据找到数组的下标
int Location(AdjListGraph gh, char c)
{if (gh.numVex <= 0) return -1;for (int i=0;i<gh.numVex;i++){if (c==gh.adjList[i].data){return i;}}return-1;
}//图的创建
void CreateALGraph(AdjListGraph &gh)
{cout << "输入图的定点数 和边数：";cin >> gh.numVex >> gh.numEdg;if (gh.numVex > MAXSIZE) return;cout << endl << "输入相关顶点： " << endl;//保存顶点for (int i=0;i<gh.numVex;i++){cin >> gh.adjList[i].data;gh.adjList[i].first = NULL;  //顶点的第一条边目前连接为空}char vi, vj;//保存输入的顶点；int i, j;cout << "请依次输入边(vi,vj)上的顶点序号：" << endl;for(int k = 0; k < gh.numEdg; k++){cin >> vi >> vj;i = Location(gh, vi);  	//获取要连接的两个点在数组中的下标j = Location(gh, vj);if (i>=0 && j>=0){   //头插法插入边EdgeNode *temp = new EdgeNode;  temp->adjvex = j;  temp->next = gh.adjList[i].first;gh.adjList[i].first = temp;}}
}

🚀三、邻接表的深度遍历

⛳（一）深度优先遍历算法原理

首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；

当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直到所有的顶点都被访问过。

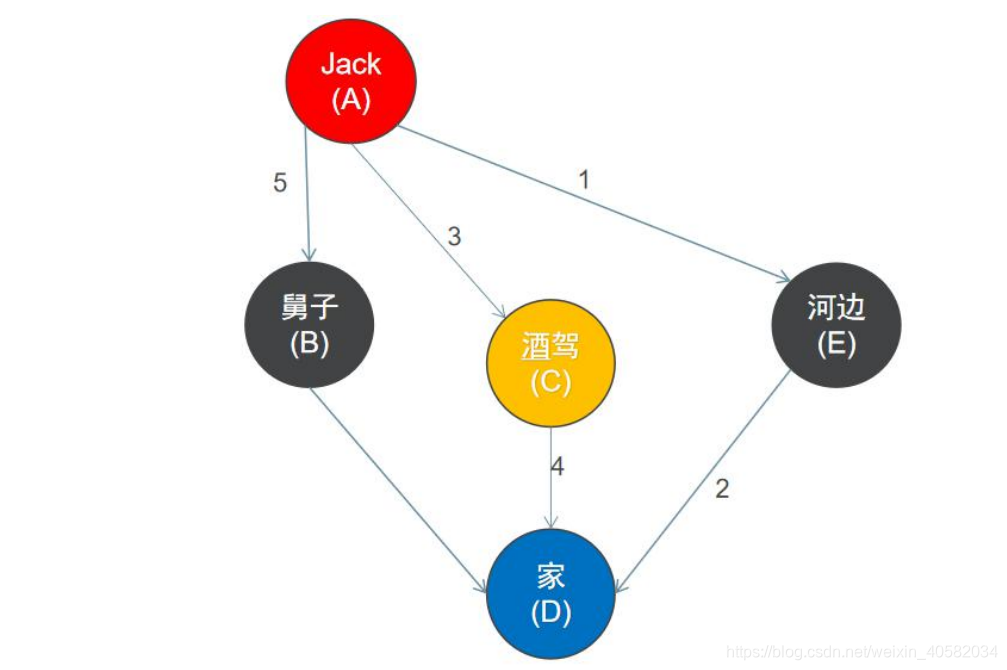
使用深度优先搜索来遍历这个图的具体过程是：

1. 首先从一个未走到过的顶点作为起始顶点，比如 A 顶点作为起点。
2. 沿 A 顶点的边去尝试访问其它未走到过的顶点，首先发现 E 号顶点还没有走到过，于是访问 E 顶点。
3. 再以 E 顶点作为出发点继续尝试访问其它未走到过的顶点，接下来访问 D 顶点。
4. 再尝试以 D 顶点作为出发点继续尝试访问其它未走到过的顶点。
5. 但是，此时沿 D 顶点的边，已经不能访问到其它未走到过的顶点，接下来返回到 E 顶点。
6. 返回到 E 顶点后，发现沿 E 顶点的边也不能再访问到其它未走到过的顶点。此时又回到顶点 A（ D-> E-> A），再以 A 顶点作为出发点继续访问其它未走到过的顶点，于是接下来访问 C 点。
7. 以此类推
8. 最终访问的结果是 A -> E -> D -> C -> B

⛳（二）深度优先遍历算法实现

bool visited[MAXSIZE] = {0};//全局数据用来判断元素是否被访问过//对图上的顶点进行深度遍历
void DFS(adjListGraph &gh,int i)
{int nextNum = -1;if (visited[i])//如果该结点已经被访问则返回 return;//访问该结点cout << gh.adjList[i].data << " ";visited[i] = true;EdgeNode *tmp = gh.adjList[i].first;while (tmp){nextNum = tmp->adjvex;if (visited[nextNum]==false){DFS(gh, nextNum);}tmp = tmp->next;}}//对所有顶点进行深度遍历
void DFS_All(AdjListGraph &gh)
{for (int i=0;i<gh.numVex;i++){if (visited[i]==false){DFS(gh, i);}}
}

🚀四、邻接表的广度遍历

⛳（一）广度优先遍历算法原理

首先以一个未被访问过的顶点作为起始顶点，访问其所有相邻的顶点;

然后对每个相邻的顶点，再访问它们相邻的未被访问过的顶点，直到所有顶点都被访问过，遍历结束。

⛳（二）广度优先遍历算法实现

//对图上的顶点进行广度遍历
void BFS(AdjListGraph &gh,int i)
{int cur = -1;queue<int> q;q.push(i);while (!q.empty())//队列不为空{cur = q.front();//取队列的头元素if (visited[cur]==false){cout << gh.adjList[cur].data << " ";visited[cur] = true;}q.pop();//取当前结点相邻的结点入队EdgeNode *tmp = gh.adjList[cur].first;while (tmp!=NULL){q.push(tmp->adjvex);tmp = tmp->next;}}
}
//对所有顶点进行广度遍历
void BFS_All(AdjListGraph &gh)
{for (int i = 0; i < gh.numVex; i++){if (visited[i] == false){BFS(gh, i);}}
}

程序清单

#include <iostream>
#include <queue>
#define MAXSIZE 1024
using namespace std;typedef struct _EdgeNode//与结点连接的边 
{int adjvex;//邻接的顶点 int weight;//权重struct _EdgeNode *next;//指向下一个顶点/边
}EdgeNode;typedef struct _VertexNode//顶点结点
{char data;//结点数据struct _EdgeNode *first;
}VertexNode,*AdjList;typedef struct _AdJListGraph
{AdjList adjList;//顶点数组int numVex;int numEdg;
}AdjListGraph;//图的初始化
bool Init(AdjListGraph &gh)
{gh.adjList = new VertexNode[MAXSIZE];//分配顶点数组地址if (!gh.adjList) return false;gh.numEdg = 0;gh.numVex = 0;}//寻找顶点的数据找到数组的下标
int Location(AdjListGraph gh, char c)
{if (gh.numVex <= 0) return -1;for (int i=0;i<gh.numVex;i++){if (c==gh.adjList[i].data){return i;}}return-1;
}//图的创建
void CreateALGraph(AdjListGraph &gh)
{cout << "输入图的定点数 和边数：";cin >> gh.numVex >> gh.numEdg;if (gh.numVex > MAXSIZE) return;cout << endl << "输入相关顶点： " << endl;//保存顶点for (int i=0;i<gh.numVex;i++){cin >> gh.adjList[i].data;gh.adjList[i].first = NULL;}char vi, vj;//保存输入的顶点；int i, j;cout << "请依次输入边(vi,vj)上的顶点序号：" << endl;for(int k = 0; k < gh.numEdg; k++){cin >> vi >> vj;i = Location(gh, vi);j = Location(gh, vj);if (i>=0 && j>=0){EdgeNode *temp = new EdgeNode;temp->adjvex = j;temp->next = gh.adjList[i].first;gh.adjList[i].first = temp;}}
}bool visited[MAXSIZE] = {0};//全局数据用来判断元素是否被访问过//对图上的顶点进行深度遍历
void DFS(AdjListGraph &gh,int i)
{int nextNum = -1;if (visited[i])//如果该结点已经被访问则返回 return;//访问该结点cout << gh.adjList[i].data << " ";visited[i] = true;EdgeNode *tmp = gh.adjList[i].first;while (tmp){nextNum = tmp->adjvex;if (visited[nextNum]==false){DFS(gh, nextNum);}tmp = tmp->next;}}//对所有顶点进行深度遍历
void DFS_All(AdjListGraph &gh)
{for (int i=0;i<gh.numVex;i++){if (visited[i]==false){DFS(gh, i);}}
}//对图上的顶点进行广度遍历
void BFS(AdjListGraph &gh,int i)
{int cur = -1;queue<int> q;q.push(i);while (!q.empty())//队列不为空{cur = q.front();//取队列的头元素if (visited[cur]==false){cout << gh.adjList[cur].data << " ";visited[cur] = true;}q.pop();//取当前结点相邻的结点入队EdgeNode *tmp = gh.adjList[cur].first;while (tmp!=NULL){q.push(tmp->adjvex);tmp = tmp->next;}}
}
//对所有顶点进行广度遍历
void BFS_All(AdjListGraph &gh)
{for (int i = 0; i < gh.numVex; i++){if (visited[i] == false){BFS(gh, i);}}
}
int main()
{AdjListGraph G;cout << "正在创建邻接表，请按提示进行输入..." << endl;Init(G);CreateALGraph(G);cout << "正在进行深度优先遍历，遍历结果如下:" << endl;//深度优先遍历DFS_All(G);cout << endl;memset(visited, 0, sizeof(visited));cout << "正在进行广度优先遍历，遍历结果如下:" << endl;//广度优先遍历BFS_All(G);cout << endl;
}