题目描述：

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

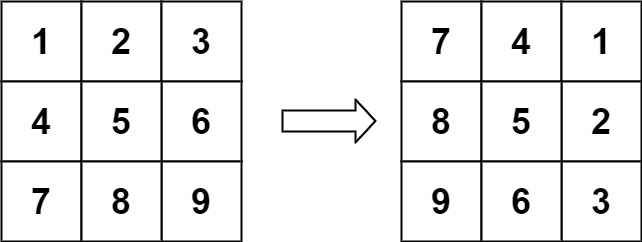
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

思路：

①我们可以把这个图分成四个区域，

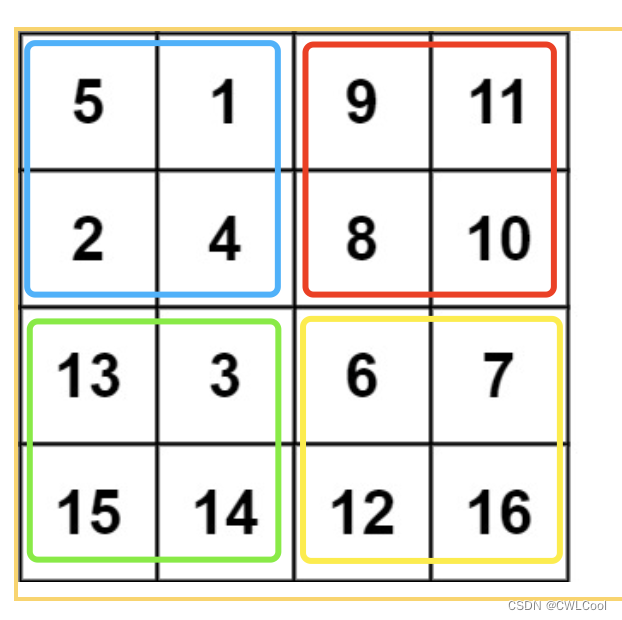
我能只要遍历第一个区域，如果行数为奇数的，向下取整

②我们可以新建一个temp变量，用于交换，相同颜色框的旋转遵循：

matrix[i][j]=matrix[n-j][i]

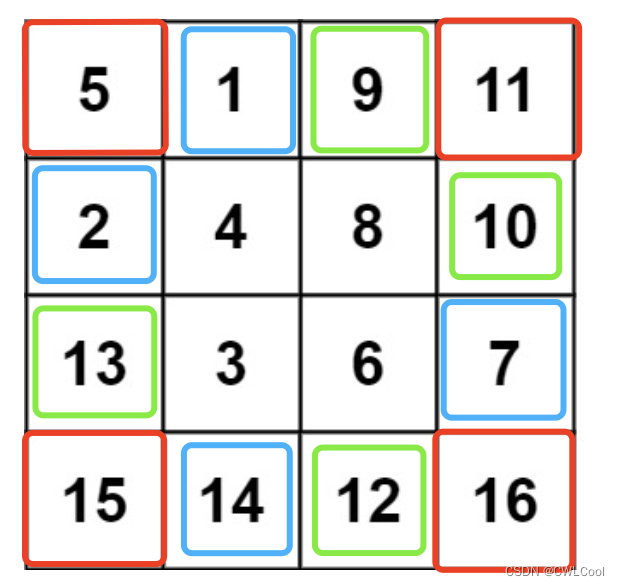
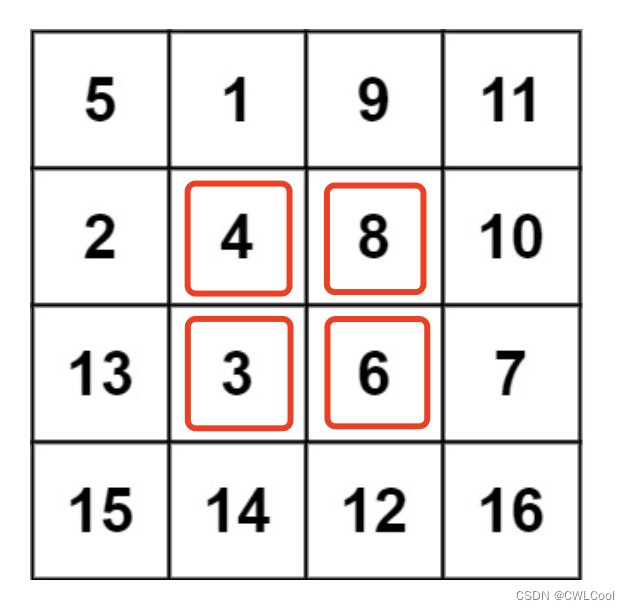
代码：

class Solution(object):def rotate(self, matrix):""":type matrix: List[List[int]]:rtype: None Do not return anything, modify matrix in-place instead."""h = len(matrix)n = h-1for i in range(h//2):for j in range(i,n-i): # 这里j表示层数，最外层是0层，内层依次增加tmp = matrix[i][j]matrix[i][j] = matrix[n-j][i]matrix[n-j][i] = matrix[n-i][n-j]matrix[n-i][n-j] = matrix[j][n-i]matrix[j][n-i]=tmp